Обзор алгоритмов поиска и распознавания простых чисел, информация об их применимости.

Содержание
Простое число
Зачем искать простые числа?
Алгоритмы поиска простых чисел
Сравнение алгоритмов поиска простых чисел
Алгоритмы распознавания простых чисел. Тесты простоты.
Сравнение тестов простоты
Список литературы

Простое число
Простое число – это натуральное число, которое имеет ровно два различных натуральных делителя: единицу и самого себя.
Остальные числа, кроме единицы, называются составными.
Последовательность простых чисел начинается так: 2, 3, 5, 7, 11, 13, 17, 19, 23 , 29, 31, …

Самое большое простое число
Один из рекордов поставил в своё время Эйлер, найдя простое число
231 − 1 = 2147483647.
Наибольшим известным простым числом по состоянию на февраль 2011 года является
243112609 − 1
За нахождение простых чисел из более чем 100 000 000 и 1 000 000 000 десятичных цифр EFF назначила денежные призы соответственно в 150 000 и 250 000 долларов.

Зачем искать простые числа?
Криптография – наука о методах обеспечения конфиденциальности (невозможности прочтения информации посторонним) и аутентичности (целостности и подлинности авторства) информации.
Криптография изучает методы шифрования информации – преобразования открытого текста на основе секретного алгоритма и/или ключа в шифрованный текст.
В криптографических алгоритмах одной из важных задач является проверка на простоту, т.е. умение быстро отличить просто число от составного.

Алгоритмы поиска
простых чисел
Простые способы нахождения начального списка простых чисел вплоть до некоторого значения дают :
Решето Эратосфена
Решето Сундарама
Решето Аткина

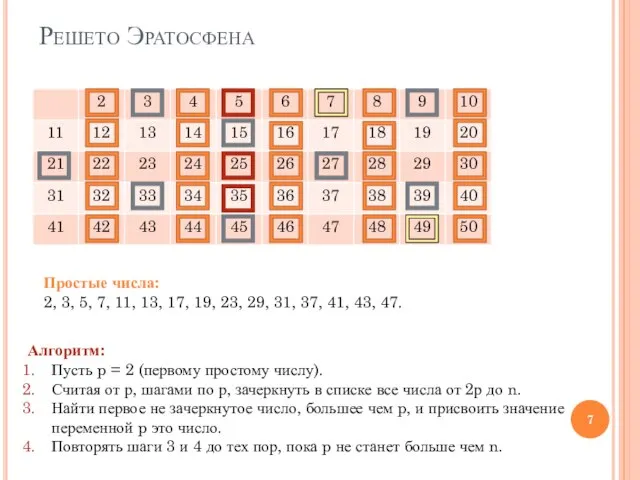
Решето Эратосфена
Алгоритм:
Пусть p = 2 (первому простому числу).
Считая от р, шагами по р, зачеркнуть в списке все числа от 2р до n.
Найти первое не зачеркнутое число, большее чем p, и присвоить значение переменной p это число.
Повторять шаги 3 и 4 до тех пор, пока p не станет больше чем n.
Простые числа:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.

Решето Эратосфена
Сложность алгоритма:

Решето Сундарама
i = 1,
j = 1,…,6;
i = 2,
j = 1,2,3;
Простые числа:
3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41.

Решето Сундарама. Обоснование
Алгоритм работает с нечётными натуральными числами большими 1, представленными в виде 2m+1, где m является натуральным числом.
Если число 2m+1 является составным, то оно представляется в виде произведения двух нечётных чисел больших единицы, то есть:
2m+1 = (2i+1)(2j+1) , где i, j – натуральные числа
m = 2ij+i+j
Что эквивалентно:
Если из ряда натуральных чисел исключить все числа вида 2ij + i + j, , то для каждого из оставшихся чисел m число 2m+1 обязано быть простым.
Если число 2m+1 является простым, то число m невозможно представить в виде 2ij+i+j и, таким образом, m не будет исключено в процессе работы алгоритма.

Решето Аткина
B основу алгоритма "решета Аткина" положены три стандартные теоремы теории элементарных чисел:
1.
2.
3.

Алгоритм
Создать решето (массив соответствия простым числам для всех положительных, целых чисел начиная с 2). Изначально все элементы решета помечаются как составные.
Для каждого числа n в решете , если остаток от деления по модулю 60:
Равен 1, 13, 17, 29, 37, 41, 49, или 53, и n = 4 * x2 + y2 поменять значение в решете на противоположное.
Равен 7, 19, 31, или 43, и n = 3 * x2 + y2; поменять значение решете на противоположное.
Равен 11, 23, 47, или 59, и n = 3 * x2 - y2 при(x > y); поменять значение в решете на противоположное.
(х и у целые, положительные числа)
Взять наименьшее число из решета, помеченное как простое, и пометить все элементы решета, кратные квадрату этого простого числа как составные.
Повторить шаг 3

Решето Аткина
Алгоритм имеет асимптотическую сложность:
и требует следующее кол-во бит памяти:

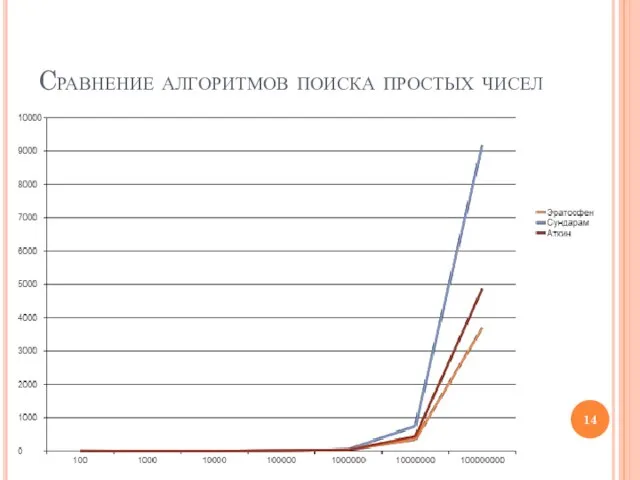
Cравнение алгоритмов поиска простых чисел

Алгоритмы распознавания простых чисел. Тесты простоты
Тест простоты — алгоритм, который по заданному натуральному числу определяет, простое ли это число.
Перебор делителей
Теорема Вильсона
Тест Ферма
Тест Пепина
Тест Миллера – Рабина
Тест Агравала – Каяла – Саксены

Перебор делителей
Перебор делителей — алгоритм тестирования простоты числа путем полного перебора всех возможных потенциальных делителей.
Алгоритм:
Перебор всех целых чисел от 2 до квадратного корня из числа n и вычисление остатка от деления n на каждое из этих чисел.
Если остаток от деления на некоторое число m равен нулю, то m является делителем n. В этом случае либо n объявляется составным, и алгоритм заканчивает работу.
По достижении квадратного корня из n и невозможности сократить n ни на одно из меньших чисел, n объявляется простым.

Теорема Вильсона
Теорема Вильсона — теорема теории чисел, которая утверждает, что
p — простое число тогда и только тогда, когда (p − 1)! + 1 делится на p

Тест Ферма
Основан на теореме Ферма, которая гласит:
Для составных p истинность равенства маловероятна.
Примечание:

Тест Пепина

Тест Миллера - Рабина
Тест Миллера - Рабина - вероятностный полиномиальный тест простоты.
Тест позволяет эффективно определять, является ли данное число составным. Однако, с его помощью нельзя строго доказать простоту числа.
Свидетели простоты и теорема Рабина
Пусть m – нечетное число большее 1. Тогда m-1 представимо в виде:
Целое число a, 1
или

Тест Миллера - Рабина
Алгоритм:
Параметром алгоритма Миллера – Рабина является количество раундов r. В каждом раунде выполняются следующие действия:
Выбирается случайное число a, 2 < a < m-1.
Если a не является свидетелем простоты числа m, то выдается ответ «m составное», и алгоритм завершается. Иначе, выбирается новое случайное число a и процедура проверки повторяется.
После нахождения r свидетелей простоты, выдается ответ «m, вероятно, простое», и алгоритм завершается.

Тест Миллера - Рабина
Сложность алгоритма :
Однако, правильность работы алгоритма не всегда является доказанной. Вероятность, что составное число не будет выявлено за время t, обычно не превосходит

Тест Агравала — Каяла — Саксены
( или тест AKS)
Универсальность: Тест AKS может использоваться для проверки простоты любых чисел.
Полиномиальность: Наибольшее время работы алгоритма ограничено полиномом от количества цифр в проверяемом числе.
Детерминизм: Алгоритм гарантирует получение ответа.
Безусловность: Корректность теста AKS не зависит от каких-либо недоказанных гипотез.

Тест Агравала — Каяла — Саксены
( или тест AKS)
Основные идеи и принципы, на котором основан алгоритм AKS:
Утверждение:

Тест Агравала — Каяла — Саксены
( или тест AKS)

Тест Агравала — Каяла — Саксены
( или тест AKS)
Сложность алгоритма AKS:
Примечание:

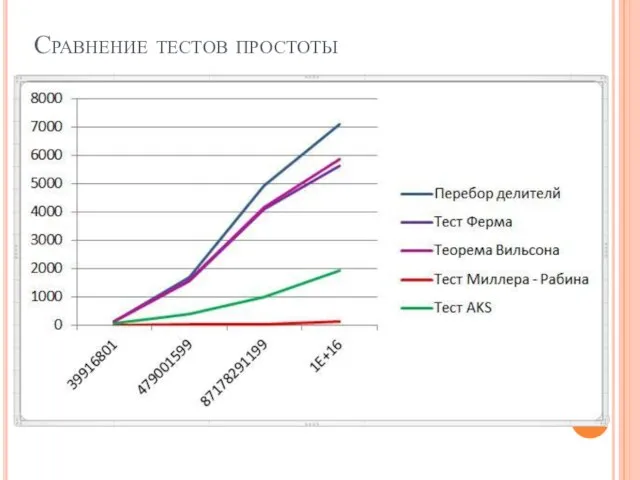
Сравнение тестов простоты

Список литературы
Википедия
Л. Бараш, Алгоритм AKS проверки чисел на простоту и поиск констант генераторов псевдослучайных чисел.
С.В. Сизый, Лекции по теории чисел.
С. Г. Гиндикин, Малая теорема Ферма / Квант. — 1972. — № 10.
A.O.L. Atkin, D.J. Bernstein, Prime sieves using binary quadratic forms. – 1999.
И.В.Агафонова, Проверка чисел на простоту: полиномиальный алгоритм.
Б.А. Фороузан, Математика криптографии и теория шифрования.