ОЦЕНКА РИСКОВ УГРОЗ ЭНЕРГЕТИЧЕСКОЙ БЕЗОПАСНОСТИ РЕГИОНА

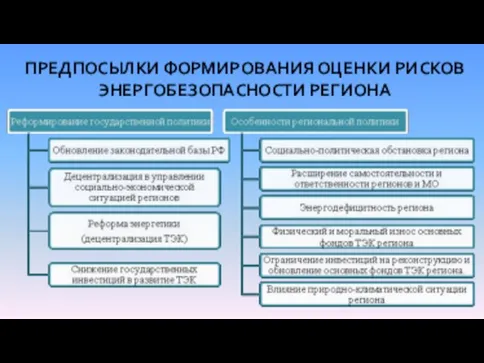
ПРЕДПОСЫЛКИ ФОРМИРОВАНИЯ ОЦЕНКИ РИСКОВ ЭНЕРГОБЕЗОПАСНОСТИ РЕГИОНА

Цель оценки энергетической безопасности региона

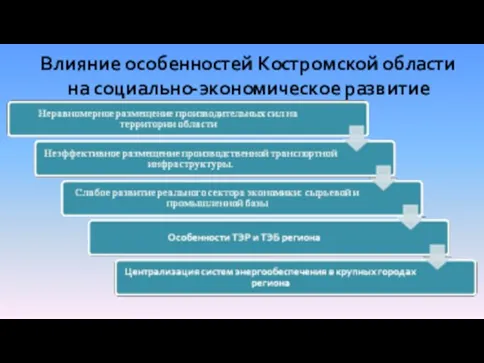
Влияние особенностей Костромской области на социально-экономическое развитие

Основные направления обеспечения энергобезопасности региона

Основные направления обеспечения энергобезопасности региона
№1 Обеспечение энергетической независимости региона

Основные направления обеспечения энергобезопасности региона
№2 Самообеспечение региона топливно-энергетическими ресурсами

Основные направления обеспечения энергобезопасности региона
№3 Мониторинг, анализ и разработка вариантов энергобезопасности

Основные направления обеспечения энергобезопасности региона
№4 Разработка региональной программы по энергетической независимости

Основные направления обеспечения энергобезопасности региона
№5 Обеспечение решения первоочередных задач по энергетической безопасности региона

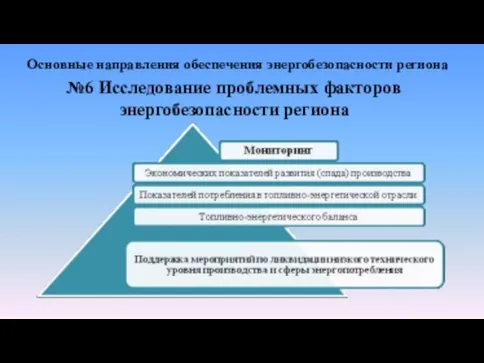
Основные направления обеспечения энергобезопасности региона
№6 Исследование проблемных факторов энергобезопасности региона

Регрессионный анализ
С помощью регрессионного анализа можно оценить средний ущерб, наносимый каждой угрозой

Se – стандартная ошибка для коэффициента m; Seb – стандартная ошибка для свободного члена b; R2 – коэффициент детерминированности, который показывает, как близко уравнение описывает исходные данные. Чем ближе он к 1, тем больше сходится теоретическая зависимость и экспериментальные данные;
Sey – стандартная ошибка для y; F – критерий Фишера определяет случайная или нет взаимосвязь между зависимой и независимой переменными; Df – степень свободы системы; Ssreg – регрессионная сумма квадратов; Ssresid – остаточная сумма квадратов
Статистические показатели линейной регрессии
С помощью спец. программы в Excel

Оценка качества модели по критериям Стьюдента и Фишера проводиться путём сравнения расчетных значений с табличными.
Для оценки качества модели по критерию Стьюдента фактическое значение этого критерия (tрасч)
tрасч = mn/ Sen ,
равнивается с критическим значением tтабл, которое рассчитывается по формуле:
tтабл=СТЬЮДРАСПОБР(0,05;n-m-1),
с учетом заданного уровня значимости (α = 0,05) и числа степеней свободы (n-m-1)
Если tрасч > tтабл, то полученное значение коэффициента корреляции признается значимым.
Для проверки адекватности модели, используют F‑критерий Фишера.
Расчётное значение тоже сравнивают с табличным и делают вывод об адекватности.
Fрасч находится в четвёртой строке первого столбца нашей таблицы. Fтабл найдём по формуле:
Fтабл = FРАСПОБР(0,05; m; n-m-1).
Математической моделью статистического распределения F-статистики является распределение Фишера с и степенями свободы
Рассчитав среднюю цену ущерба всех угроз (С), мы теперь можем определить величину потерь от воплощения угроз за определённый период ∆t (за 1 месяц, за 2 месяца, …, за 12 месяцев).

Критерий Байеса
Критерий Байеса может использоваться в двух видах: как критерий максимума среднего выигрыша или как критерий минимума среднего риска. В нашем случае, выбирается критерий минимума, так как речь идет о затратах на оборудование и, соответственно, чем они меньше, тем лучше для предприятия.
Оценки решений по критерию минимума среднего
риска находятся по следующей формуле:
Zi = ∑ Rij Pj , i=1,...,m, j=1,...,n.
Лучшим является решение с минимальной оценкой:
Z* = min Zi

Вероятность наступления k событий за
некоторый интервал времени Δt определяется
законом (распределением) Пуассона:
Pk = (λ·Δt) k · exp (–λ·Δt) / k!
Поток Пуассона
Поток Пуассона – это один из наиболее распространённых видов потока заявок.
Поток заявок – поток событий, распределенных во времени, т.е. последовательность однородных событий, следующих одно за другим в некоторые моменты времени. В общем случае он рассматривается как случайный процесс, задаваемый функцией распределения промежутков времени между моментами поступления двух соседних заявок.

метод STEM
Формирование матрицы парных сравнений
В каждую ячейку которой Cij заносится максимальное значение j-гo критерия эффективности при оптимизации
по i-му критерию. При этом необходимо обеспечить
Нормирование значений критериев, когда их наибольшее значение равно единице, а наименьшее – нулю
Относительные значения критериев
Полученная матрица содержит ценную информацию для ЛПР. Так, если значения каких-то двух столбцов близки для каждой из строк, то два соответствующих критерия сильно зависимы, так как изменения любых других критериев одинаково влияют на них. Можно выявить также и противоречивые критерии, когда высокая оценка по одному сопровождается низкой оценкой по другому

Вычисляются средние значения aj,
взятые по всем элементам j-го столбца
(кроме диагональных):
Индексы критериев эффективности lj
Данные индексы также называют коэффициентами внимания или техническими весами критериев, так как он вычисляется, а не назначается через экспертную оценку.

Индексы λj позволяют сформировать комплексную целевую функцию:
где Ci и li – соответственно текущее значение и технический вес i-го критерия эффективности.
Далее происходит поиск лучшей комбинации значений критериев в соответствии с выявленной целевой функцией
Такой способ определения технических весов отражает стремление найти в области допустимых решений вершину с наилучшими значениями по всем критериям.

Поиск лучшей комбинации значений критериев в соответствии с выявленной целевой функцией по алгоритму