Описание и преобразование управляющих процессов

Основная задача начального этапа проектирования УА – выбор формализованного языка.
Основные понятия – базис сетей Петри:
событие;
условие.
Сеть Петри – структура УП
↓
это последовательность
процедур
Условия → событие
Состояние системы – это множество условий
Событие → новые условия →
→ изменение состояния системы
События – множество переходов
T={t0, t1, …, tr}
Условия – множество позиций
A={a0, a1, …, af}
I – входная функция
связь T и A
O – выходная функция
I – отображает tv(v=0 r) в мн-во позиций I(tv) – входные позиции перехода
O – отображает tv в мн-во позиций O(tv) – выходные позиции перехода
aµ - входная позиция tv, если aµ ϵ I(tv)
aµ - выходная позиция tv, если aµϵO(tv)
Сеть Петри – N = (A, T, I, O)

Пример:
A = {a0, a1, a2, a3, a4}
T = {t0, t1, t2, t3, t4}
I(t0) = a0 I(t1) = a1
I(t2) = a2 I(t3) = a3
I(t4) = a4
O(t0) = a1 O(t1) = a2
O(t2) = a3 O(t3) = a4
I – матрица следования
O – матрица предшествования
Графическое представление
сети Петри
Типы вершин:
позиции – «O»
переходы – «–»
if (aµ - вход для tv), then (дуга aµ→ tv)
if (aµ - выход для tv), then (дуга tv→ aµ)
↓
G = (V, W) – ориентированный двудольный мультиграф, где
V – множество вершин
W – множество направленных дуг
V = A U T A ∩ T = Ø
позиция – условие
↓
Выполнение условия – маркировка позиции
(метка – «точка» в позиции)
↓
ʘ
↓
Если несколько точек –
то «емкость условия»

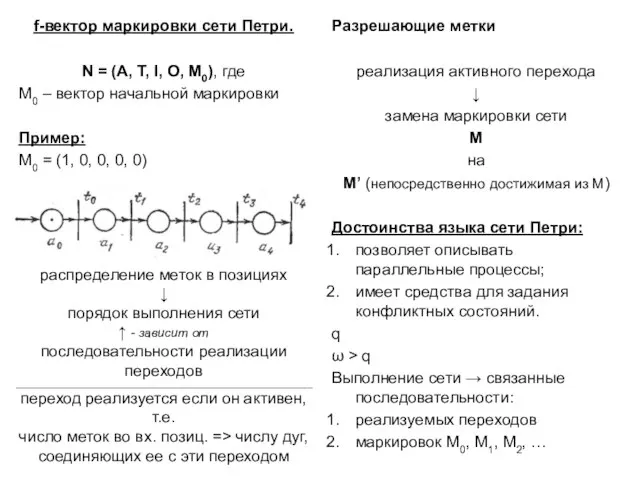
f-вектор маркировки сети Петри.
N = (A, T, I, O, M0), где
M0 – вектор начальной маркировки
Пример:
M0 = (1, 0, 0, 0, 0)
Разрешающие метки
реализация активного перехода
↓
замена маркировки сети
M
на
M’ (непосредственно достижимая из M)
Достоинства языка сети Петри:
позволяет описывать параллельные процессы;
имеет средства для задания конфликтных состояний.
q
ω > q
Выполнение сети → связанные последовательности:
реализуемых переходов
маркировок M0, M1, M2, …
распределение меток в позициях
↓
порядок выполнения сети
↑ - зависит от
последовательности реализации
переходов
___________________________________________________________________________
переход реализуется если он активен,
т.е.
число меток во вх. позиц. => числу дуг,
соединяющих ее с эти переходом

Безопасная сеть Петри.
запрещено наличие кратных дуг между позициями и переходами;
вектор маркировки может содержать лишь 0 и 1;
реализация активного перехода возможна, если ни 1 из его выходных позиций не содержит меток – число меток в любой позиции не больше 1;
конечное число состояний – 2f при f позициях.
Ограниченная сеть Петри.
k → k-безопасная позиция или k-ограниченная
k’ >= k – k’-безопасной
kmax
Ограничение оригинальной сети Петри – моделирование примитивных событий.
________________________________
это сеть позиция-переход
↓
автоматная сеть
↓
маркированный граф
________________________________
сети с предикатами на переходах
↓
расширение ее описательных возможностей
________________________________
Введение позиции времени в сети Петри.
Временные сети: переход – t;
Тайм-аутные сети: переход – a и b.

Тайм-аутные сети Петри.
0<=a<=b
q
(q+a) (q+b)
Помеченные сети Петри.
метка – цвет
1 позиция – несколько цветов
Численные сети Петри.
метки любой природы и величины;
условия активизация и результата реализации независимы;
при реализации переходов изменяется маркировка входных и выходных позиций и содержимое памяти данных
Использование дуг разных типов в сети Петри.
Существуют:
Простые дуги:
1.1. активизирующая;
1.2. сдерживающая;
1.3. входная;
1.4. выходная;
Составные дуги:
2.1. активизирующая входная;
2.2. сдерживающая выходная.

Управляющие процессы и их формализованное описание.

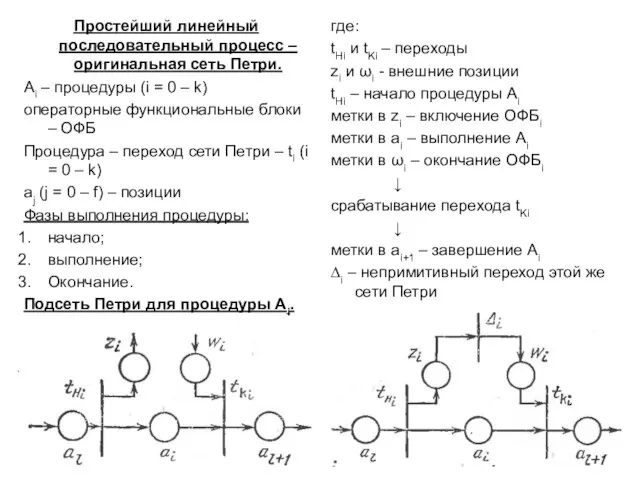
Простейший линейный последовательный процесс – оригинальная сеть Петри.
Ai – процедуры (i = 0 – k)
операторные функциональные блоки – ОФБ
Процедура – переход сети Петри – ti (i = 0 – k)
aj (j = 0 – f) – позиции
Фазы выполнения процедуры:
начало;
выполнение;
Окончание.
Подсеть Петри для процедуры Ai.
где:
tHi и tKi – переходы
zi и ωi - внешние позиции
tHi – начало процедуры Ai
метки в zi – включение ОФБi
метки в ai – выполнение Ai
метки в ωi – окончание ОФБi
↓
срабатывание перехода tKi
↓
метки в ai+1 – завершение Ai
∆i – непримитивный переход этой же сети Петри

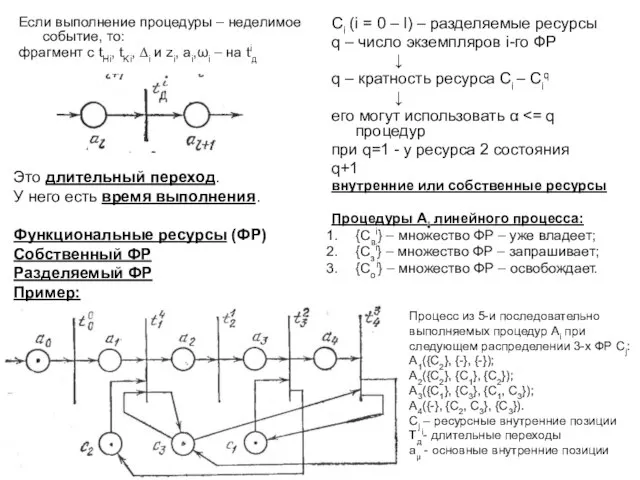
Если выполнение процедуры – неделимое событие, то:
фрагмент с tHi, tKi, ∆i и zi, ai,ωi – на tiд
Ci (i = 0 – l) – разделяемые ресурсы
q – число экземпляров i-го ФР
↓
q – кратность ресурса Ci – Ciq
↓
его могут использовать α <= q процедур
при q=1 - у ресурса 2 состояния
q+1
внутренние или собственные ресурсы
Процедуры Ai линейного процесса:
{Cвi} – множество ФР – уже владеет;
{Cзi} – множество ФР – запрашивает;
{Cоi} – множество ФР – освобождает.
Это длительный переход.
У него есть время выполнения.
Функциональные ресурсы (ФР)
Собственный ФР
Разделяемый ФР
Пример:
Процесс из 5-и последовательно
выполняемых процедур Ai при
следующем распределении 3-х ФР Cj:
A1({C2}, {-}, {-});
A2({C2}, {C1}, {C2});
A3({C1}, {C3}, {C1, C3});
A4({-}, {C2, C3}, {C3}).
Сj – ресурсные внутренние позиции
Tдi- длительные переходы
aµ - основные внутренние позиции

Пример:
Если для Ai – {Cвi}=C1, {Cзi}=C3, C4 и {Cоi}=C1, C4,
то Ai({C1}, {C3, C4}, {C1, C4})
{Cзi}∩{Cвi}=Ø
Иногда: {Cвi}=Ø и {Cзi}={Cоi}
Особенности описания параллельного линейного процесса в сети Петри.
длительные переходы – процедуры;
tR – переходы распараллеливания;
tS – переходы соединения;
наличие элементарных подпроцессов;
cобственные ФР подпроцесса
Пример:

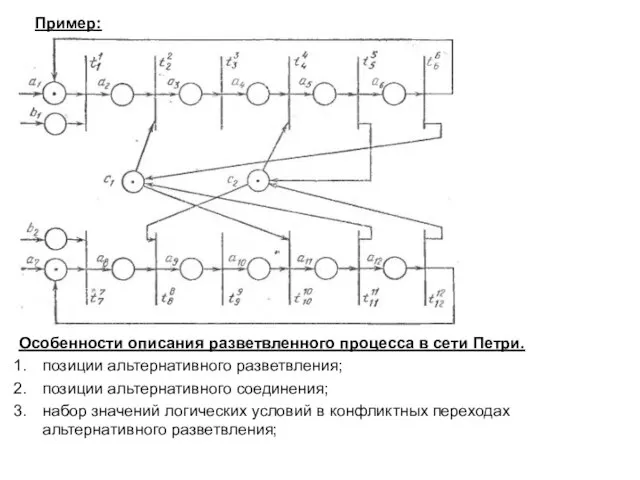
Пример:
Особенности описания разветвленного процесса в сети Петри.
позиции альтернативного разветвления;
позиции альтернативного соединения;
набор значений логических условий в конфликтных переходах альтернативного разветвления;

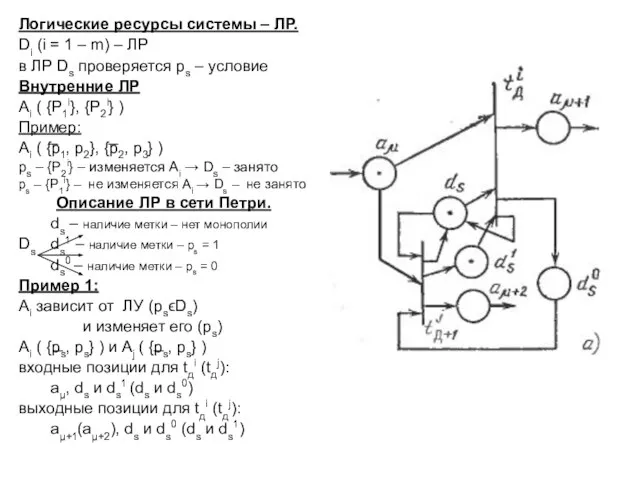
Логические ресурсы системы – ЛР.
Di (i = 1 – m) – ЛР
в ЛР Ds проверяется ps – условие
Внутренние ЛР
Ai ( {P1i}, {P2i} )
Пример:
Ai ( {p1, p2}, {p2, p3} )
ps – {P2i} – изменяется Ai → Ds – занято
ps – {P1i} – не изменяется Ai → Ds – не занято
Описание ЛР в сети Петри.
ds – наличие метки – нет монополии
Ds ds1 – наличие метки – ps = 1
ds0 – наличие метки – ps = 0
Пример 1:
Ai зависит от ЛУ (psϵDs)
и изменяет его (ps)
Ai ( {ps, ps} ) и Aj ( {ps, ps} )
входные позиции для tдi (tдj):
aµ, ds и ds1 (ds и ds0)
выходные позиции для tдi (tдj):
aµ+1(aµ+2), ds и ds0 (ds и ds1)

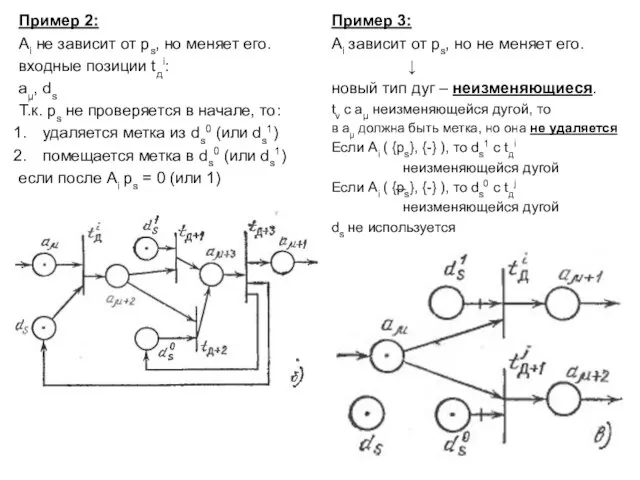
Пример 2:
Ai не зависит от ps, но меняет его.
входные позиции tдi:
aµ, ds
Т.к. ps не проверяется в начале, то:
удаляется метка из ds0 (или ds1)
помещается метка в ds0 (или ds1)
если после Ai ps = 0 (или 1)
Пример 3:
Ai зависит от ps, но не меняет его.
↓
новый тип дуг – неизменяющиеся.
tv c aµ неизменяющейся дугой, то
в aµ должна быть метка, но она не удаляется
Если Ai ( {ps}, {-} ), то ds1 c tдi
неизменяющейся дугой
Если Ai ( {ps}, {-} ), то ds0 c tдj
неизменяющейся дугой
ds не используется

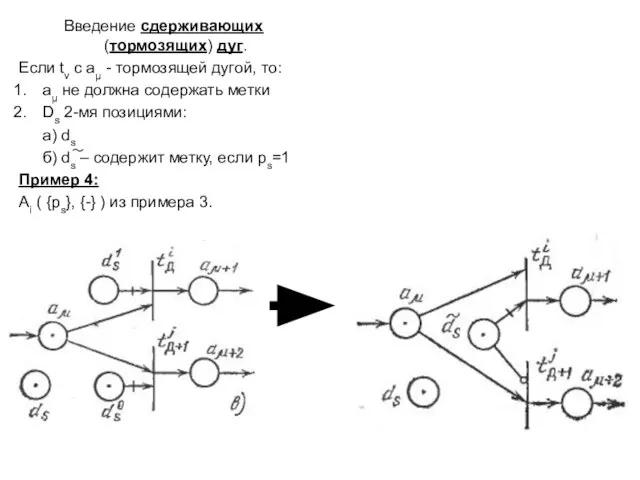
Введение сдерживающих (тормозящих) дуг.
Если tv c aµ - тормозящей дугой, то:
aµ не должна содержать метки
Ds 2-мя позициями:
а) ds
б) ds – содержит метку, если ps=1
Пример 4:
Ai ( {ps}, {-} ) из примера 3.

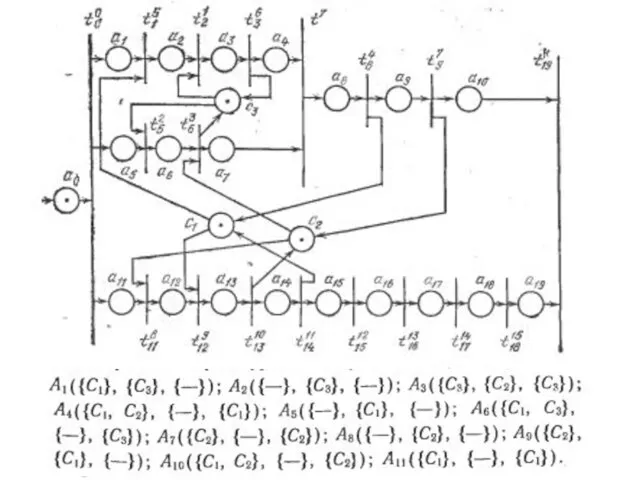
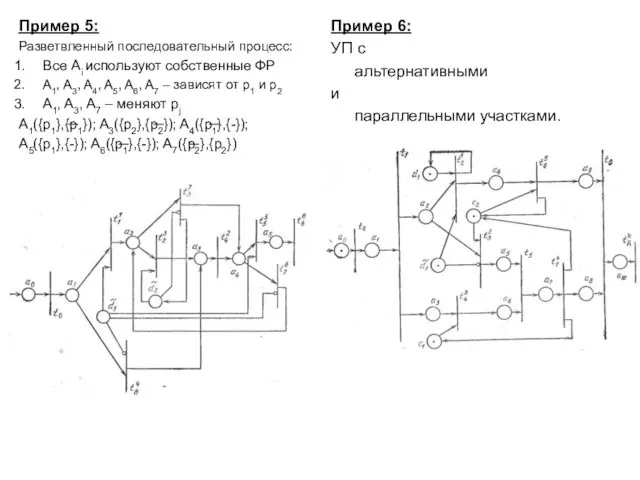
Пример 5:
Разветвленный последовательный процесс:
Все Ai используют собственные ФР
A1, A3, A4, A5, A6, A7 – зависят от p1 и p2
A1, A3, A7 – меняют pj
A1({p1},{p1}); A3({p2},{p2}); A4({p1},{-});
A5({p1},{-}); A6({p1},{-}); A7({p2},{p2})
Пример 6:
УП с
альтернативными
и
параллельными участками.

Обобщенная сеть Петри для описания неавтономного управляющего процесса.

Автономный УП
Неавтономный УП
Описание неавтономного процесса:
внеш. ЛУ (pu) ↔ внеш. позиция hu – метка есть, если pu=1; нет при pu=0
внеш. ЛУ ϵ {P1}
есть внутренние и внешние ЛУ
если Ai выполняется при pu=1 (0), то hu соединяется с tдi сдерживающей дугой
не включается позиция состояния внешнего ЛР
развитие процесса – зависит от начальной маркировки внутренних позиций и текущей маркировки внешних входных позиций
замена внешних входных позиций на предикаты, зависящие от внешних ЛУ
Если не определено влияние Ai на значение ps:
возможное изменение ps – это безразличное значение (ps) в {P2i}
позиция состояния Ds - в описании параллельного процесса
на время выполнения tдi метка из ds удаляется
позиция ds аналогична внешней позиции

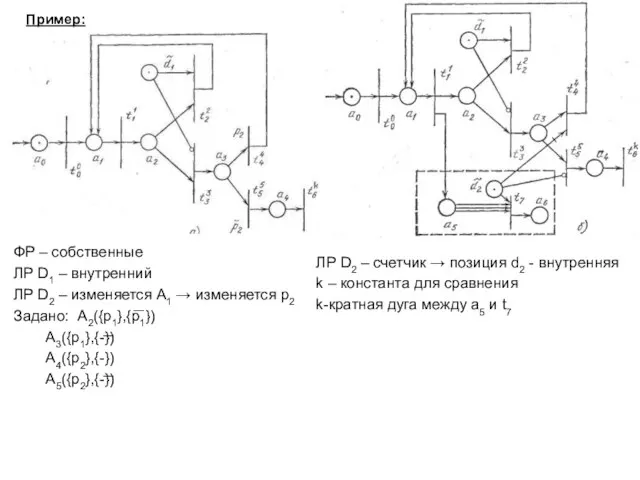
Пример:
ФР – собственные
ЛР D1 – внутренний
ЛР D2 – изменяется A1 → изменяется p2
Задано: A2({p1},{p1})
A3({p1},{-})
A4({p2},{-})
A5({p2},{-})
ЛР D2 – счетчик → позиция d2 - внутренняя
k – константа для сравнения
k-кратная дуга между a5 и t7

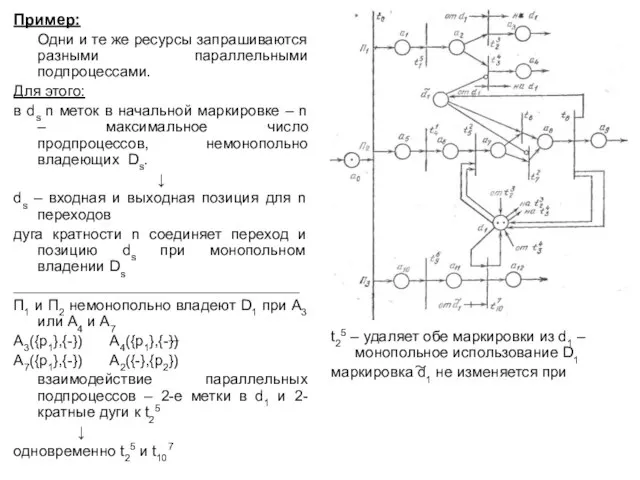
Пример:
Одни и те же ресурсы запрашиваются разными параллельными подпроцессами.
Для этого:
в ds n меток в начальной маркировке – n – максимальное число продпроцессов, немонопольно владеющих Ds.
↓
ds – входная и выходная позиция для n переходов
дуга кратности n соединяет переход и позицию ds при монопольном владении Ds
__________________________________
П1 и П2 немонопольно владеют D1 при A3 или A4 и А7
A3({p1},{-}) A4({p1},{-})
A7({p1},{-}) A2({-},{p2})
взаимодействие параллельных подпроцессов – 2-е метки в d1 и 2-кратные дуги к t25
↓
одновременно t25 и t107
t25 – удаляет обе маркировки из d1 – монопольное использование D1
маркировка d1 не изменяется при

Граф обобщенной сети Петри содержит:
длительные переходы
примитивные переходы
основные внутренние позиции
ресурсные внутренние позиции
основные дуги
неизменяющие дуги заданной
сдерживающие дуги кратности
длительный переход – это процедура
предикаты у tдi, если Ai зависит от внешних ЛУ
примитивные переходы – переходы распараллеливания и соединения – задание структуры процесса
маркировка aµ (основные) и cj, ds, ds (внутренние ресурсные) – полное состояние УП
дуги – последовательность выполнения процедур и их взаимодействие с ФР и ЛР.
Свойства:
Временных сетей с переходами, помеченными предикатами и операциями, и дугами разных типов.
Особенность:
1. в описание процесса вводятся используемые им ресурс
2. учитывается влияние процедур процесса на состояние ресурсов

Получение правильного управляющего процесса.
Граф достижимых маркировок сети Петри.

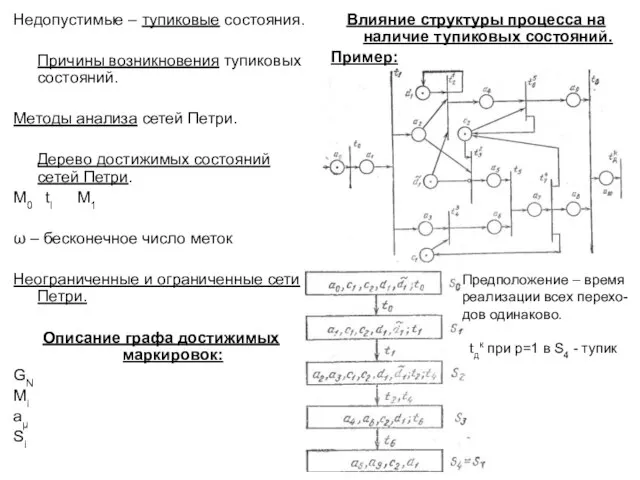
Недопустимые – тупиковые состояния.
Причины возникновения тупиковых состояний.
Методы анализа сетей Петри.
Дерево достижимых состояний сетей Петри.
М0 tl М1
ω – бесконечное число меток
Неограниченные и ограниченные сети Петри.
Описание графа достижимых маркировок:
GN
Mi
aµ
Si
Влияние структуры процесса на наличие тупиковых состояний.
Пример:
Предположение – время
реализации всех перехо-
дов одинаково.
tдк при p=1 в S4 - тупик

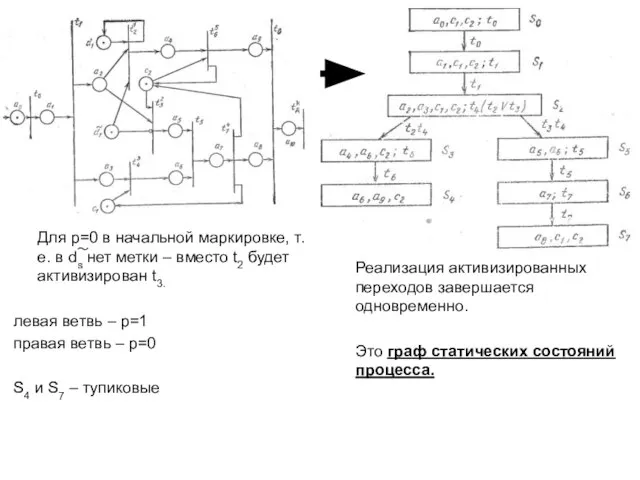
Для p=0 в начальной маркировке, т.е. в ds нет метки – вместо t2 будет активизирован t3.
левая ветвь – p=1
правая ветвь – p=0
S4 и S7 – тупиковые
Реализация активизированных переходов завершается одновременно.
Это граф статических состояний процесса.

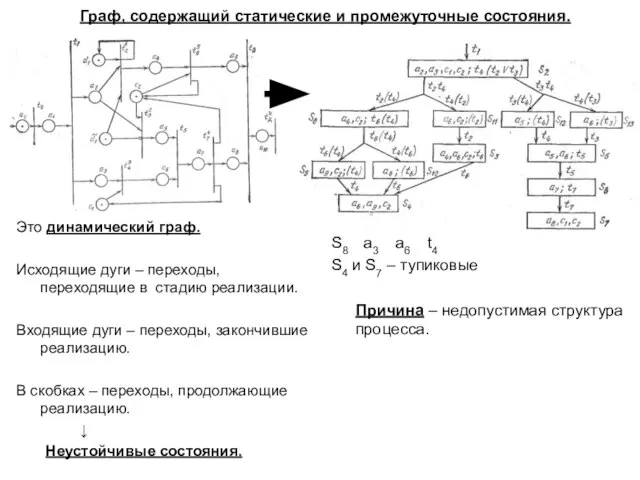
Это динамический граф.
Исходящие дуги – переходы, переходящие в стадию реализации.
Входящие дуги – переходы, закончившие реализацию.
В скобках – переходы, продолжающие реализацию.
↓
Неустойчивые состояния.
S8 a3 a6 t4
S4 и S7 – тупиковые
Причина – недопустимая структура процесса.
Граф, содержащий статические и промежуточные состояния.

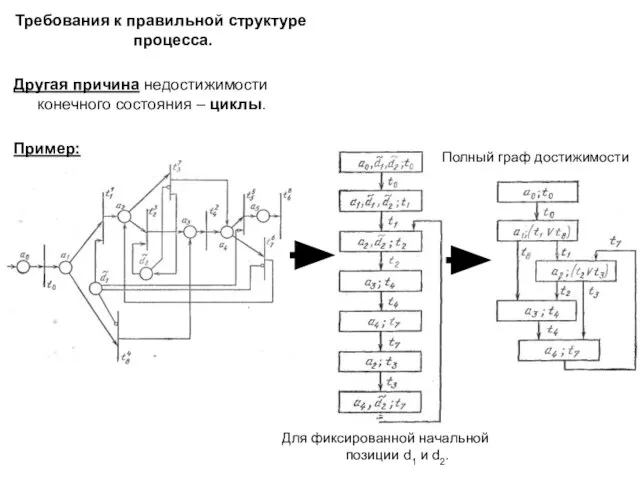
Требования к правильной структуре процесса.
Другая причина недостижимости конечного состояния – циклы.
Пример:
Для фиксированной начальной позиции d1 и d2.
Полный граф достижимости

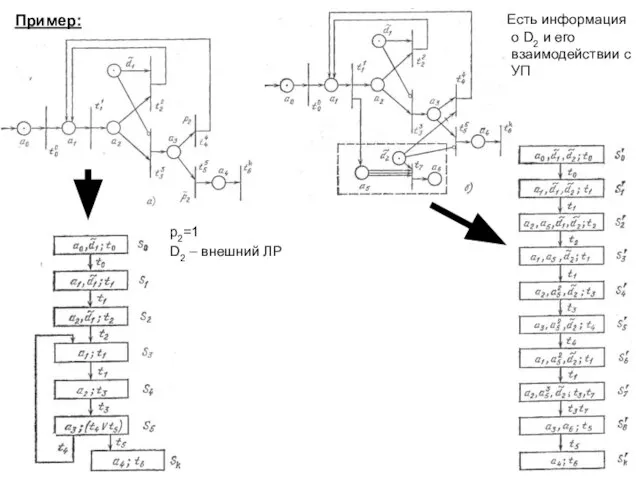
Пример:
p2=1
D2 – внешний ЛР
Есть информация о D2 и его взаимодействии с УП

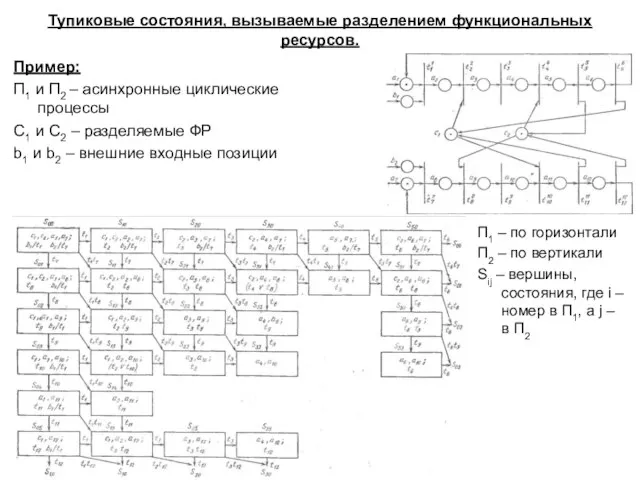
Тупиковые состояния, вызываемые разделением функциональных ресурсов.
Пример:
П1 и П2 – асинхронные циклические процессы
С1 и С2 – разделяемые ФР
b1 и b2 – внешние входные позиции
П1 – по горизонтали
П2 – по вертикали
Sij – вершины, состояния, где i – номер в П1, а j – в П2

Классификация состояний в графе достижимых маркировок сети Петри.
Состояние блокировки – Sб:
aµ ti
Состояние взаимной блокировки – Sв.б
Состояние полной взаимной блокировки – Sп.в.б
Тупиковое состояние – Sт –
это Sв.б и Sп.в.б
Предтупиковое состояние – Sп.т
Qз{Sт, Sп.т} – множество запрещенных состояний
Опасное состояние - Sоп, если:
Sv ребро Su
и
SvϵQз, а SuϵQз
Qоп – множество опасных состояний
Безопасное состояние
Состояние конфликта – Sкн
Опасные отрезки пути в графе
Корень опасных отрезков – Sк.оп
Дополнительная блокирующая позиция – аб