ОПРЕДЕЛЕНИЕ

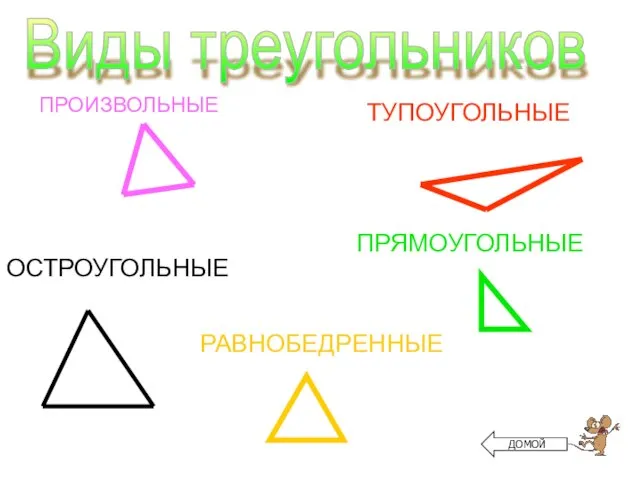
ПРОИЗВОЛЬНЫЕ
ТУПОУГОЛЬНЫЕ
ПРЯМОУГОЛЬНЫЕ
ОСТРОУГОЛЬНЫЕ
РАВНОБЕДРЕННЫЕ
ДОМОЙ
Виды треугольников

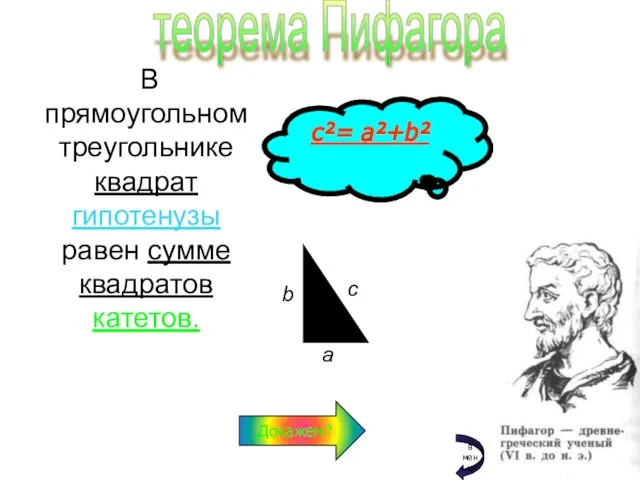
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
теорема Пифагора
с²= а²+b²
Докажем?
в меню

Рассмотрим прямоугольный треугольник
с катетами a, b и гипотенузой c. Достроим треугольник до квадрата со стороной
a + b так, как показано на рисунке.
Площадь этого квадрата равна (a +b)²
С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников.
Площадь каждого из равна ½ab.
Площадь квадрата S=4*½ ab+c²= 2ab+c²
Таким образом, (a+b)²=2ab+c², откуда c²=a²+b².
a
a
b
b
bb
c
c
c
c
a
a
b
ДОКАЗАТЕЛЬСТВО
в меню
ДОМОЙ

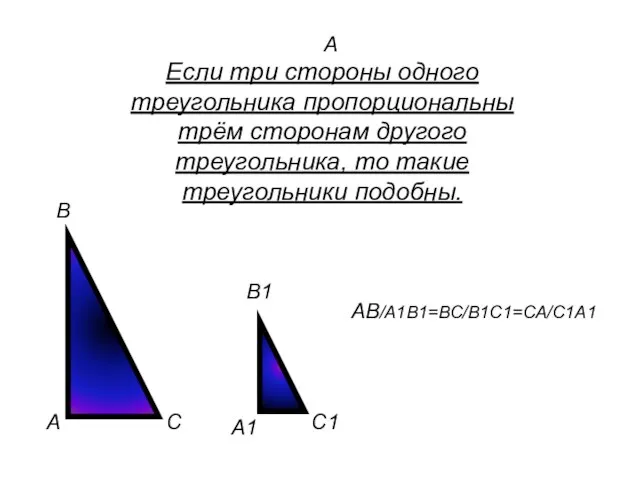
А
Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
А
А1
В
В1
С1
С
АВ/A1B1=BC/B1C1=CA/C1A1

S
S`
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
ТЕОРЕМА
S : S` = R²
Докажем?

– это треугольники, у которых 2 угла равны соответственно, а стороны пропорциональны сходственным сторонам.
подобные треугольники
ДОМОЙ
в меню