Тема” Треугольник”

Основополагающий вопрос:
Из каких частей состоит слово «многоугольник»?

Проблемные вопросы:
Какая фигура является треугольником?
Какие треугольники бывают?
Как найти сумму углов треугольника?

Цели и задачи:
Познакомить учащихся со свойствами геометрической фигуры « треугольник » развивать геометрическую интуицию.

Сроки проекта
На изучение темы ” Треугольник ” отводится две недели.

Мы познакомимся с интересным и загадочным многоугольником. Но прежде чем узнать, с какой фигурой мы будем работать, ответьте на вопросы: из каких частей состоит слово многоугольник (много углов).

Вместо слова ” много” поставить число 7. какая фигура получится? Теперь поставьте число 5. Что получилось? Слово ” многоугольник ” указывает на то, что у всех фигур из этого семейства много углов. Но для характеристики фигуры этого недостаточно.

Например, у изображенной фигуры тоже много углов, но она не является многоугольником. Как вы думаете почему? (говоря о многоугольнике, мы должны сказать, что фигура должна быть ограниченна замкнутой ломаной линией, звенья, которые не пересекают друг друга).

Давайте посмотрим на фигуру, о которой мы будем говорить.
Отметим в тетради три точки так, чтобы они не лежали на одной прямой и соединим попарно эти точки. Какая фигура у нас получилась?

Самым простым многоугольником является треугольник. Но простым, не значит интересным. Мы познакомимся поближе с геометрической фигурой из семейства многоугольников – треугольником.

Давайте посмотрим, что преподносит нам знакомство с треугольниками. Все большое семейство треугольников можно разделить на две группы: первую группу различают по числу равных сторон, а вторую – в зависимости от величины сторон.

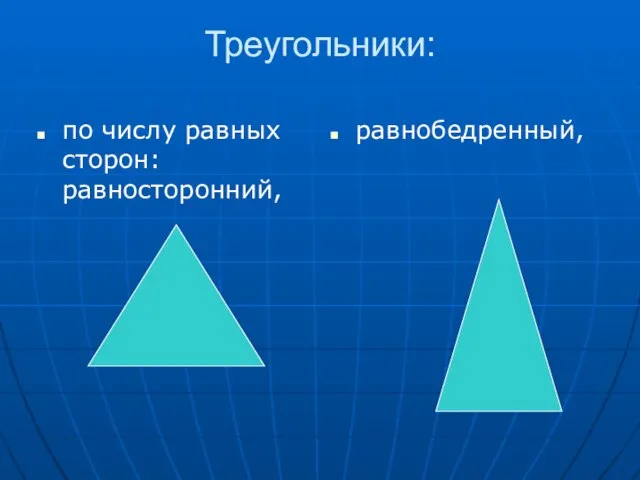
Треугольники:
по числу равных сторон: равносторонний,
равнобедренный,

разносторонний.

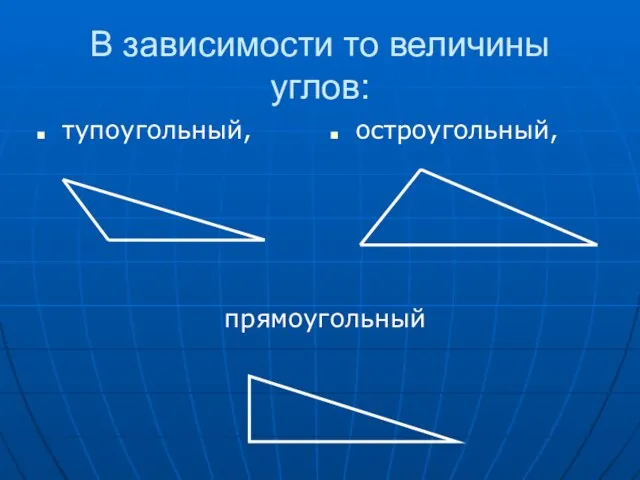
В зависимости то величины углов:
тупоугольный,
остроугольный,
прямоугольный

Каждый ученик получает треугольник. Измеряют стороны треугольника. Что вы можете сказать о сумме двух сторон по отношению к третьей сторон? Запишем первое свойство треугольника.

Сумма двух сторон треугольника всегда больше третьей стороны.
Могут ли быть у треугольника стороны равны числам 2, 2 и 5? (нет ).
Как вы думаете, чему будет равна сумма углов в треугольнике? Сейчас выполним задание и ответим на вопрос.

Задание:
оторвите углы у треугольника и сложите.
найдите сумму оторванных углов
какой угол вы получили?

Чему равны величины углов?
Итак, какой вывод можно сделать?

Запишем второе свойства. Сумма углов любого треугольника равна 1800.
Можно ли быть уверенным, что в каждом треугольнике сумма углов равна 1800? (да).
Можно ли изменить углы любого треугольника? (нет. Например, существует Бермудский треугольник, который находится в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и Полуостровом Флорида, у которого невозможно изменить углы (показать на корте). Как можно назвать равнобедренный треугольник, у которого основание равно боковой стороне? (равносторонний). Существует ли треугольник, у которого два прямых угла? (нет, т.к. сумма двух углов уже равна 1800).