Содержание
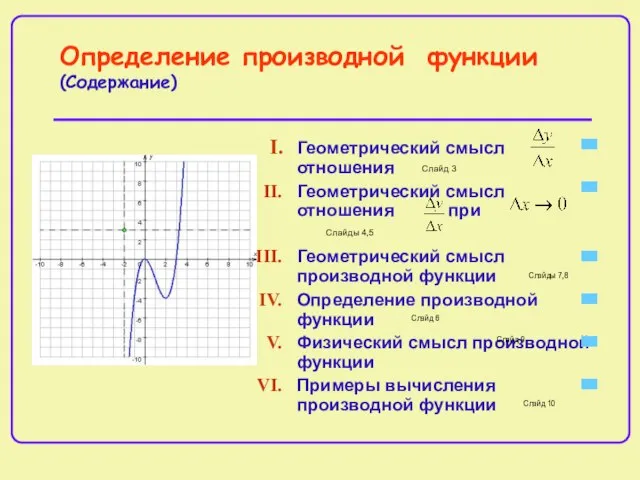
- 2. Определение производной функции (Содержание) Геометрический смысл отношения Геометрический смысл отношения при Геометрический смысл производной функции Определение
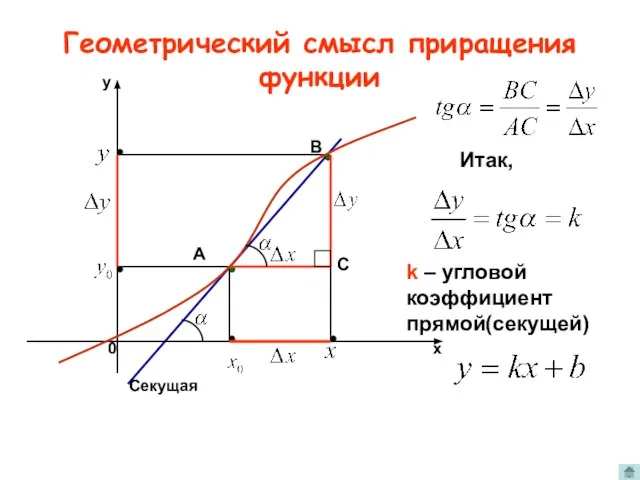
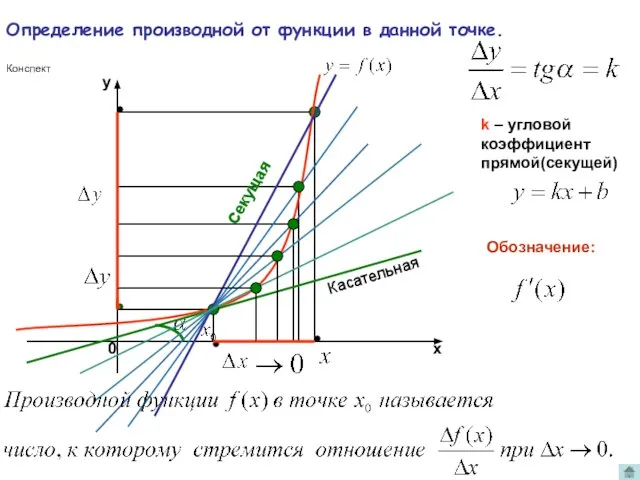
- 3. Геометрический смысл приращения функции A B Секущая С Итак, k – угловой коэффициент прямой(секущей)
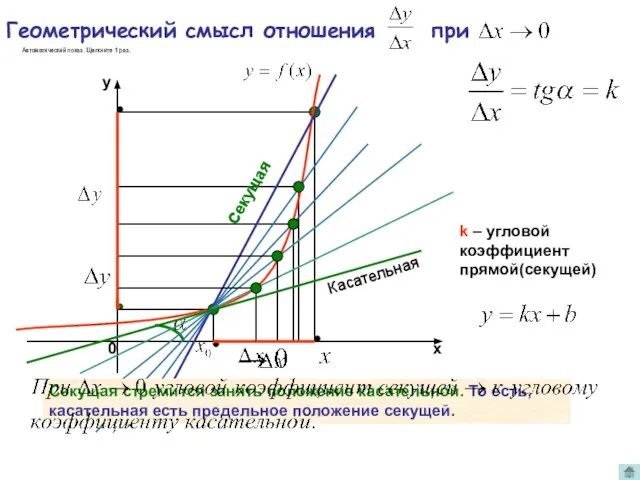
- 4. Геометрический смысл отношения при k – угловой коэффициент прямой(секущей) Секущая стремится занять положение касательной. То есть,
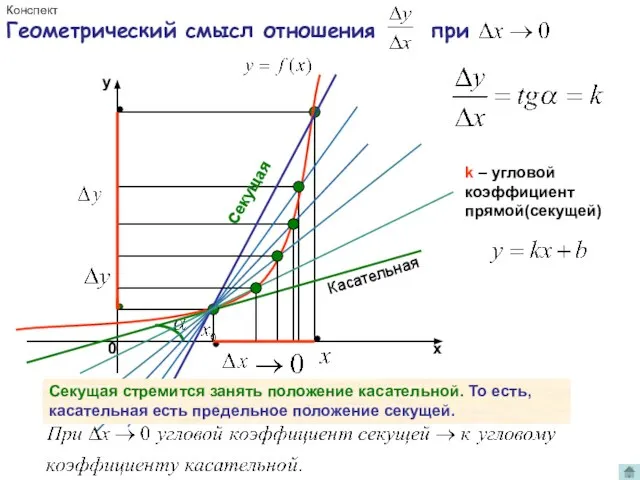
- 5. k – угловой коэффициент прямой(секущей) Секущая стремится занять положение касательной. То есть, касательная есть предельное положение
- 6. Определение производной от функции в данной точке. k – угловой коэффициент прямой(секущей) Касательная Секущая Конспект
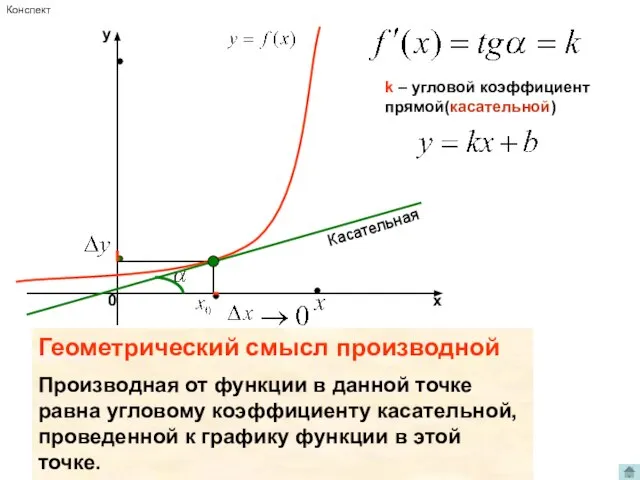
- 7. k – угловой коэффициент прямой(касательной) Касательная Геометрический смысл производной Производная от функции в данной точке равна
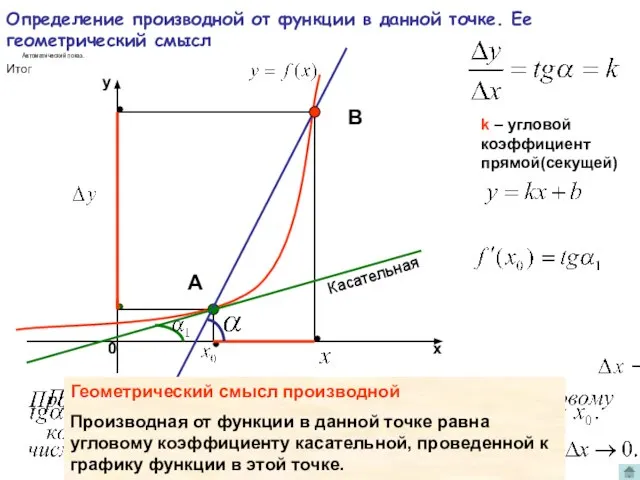
- 8. Определение производной от функции в данной точке. Ее геометрический смысл k – угловой коэффициент прямой(секущей) А
- 9. Физический смысл производной функции в данной точке .
- 11. Скачать презентацию

 Юридическое сопровождение участия в государственных и коммерческих закупках
Юридическое сопровождение участия в государственных и коммерческих закупках Великие русские художники и их картины
Великие русские художники и их картины Медицинское страхование в США
Медицинское страхование в США Международный день мира
Международный день мира Охрана окружающей среды Великобритании
Охрана окружающей среды Великобритании Как готовиться к ГИА-9 по математике
Как готовиться к ГИА-9 по математике IFB_M. Раскручиваем сайты. Держитесь крепче! Реклама в интернете. Наши услуги.
IFB_M. Раскручиваем сайты. Держитесь крепче! Реклама в интернете. Наши услуги. Prezentatsia
Prezentatsia Реконструкция набережной Тюмень
Реконструкция набережной Тюмень Презентация Джулай
Презентация Джулай Flash память
Flash память Методическое обеспечение расчетов тарифов во исполнение новых правил оптового и розничного рынков переходного периода
Методическое обеспечение расчетов тарифов во исполнение новых правил оптового и розничного рынков переходного периода Вселенная
Вселенная  К доске
К доске Самоконтроль его основные методы, показатели и критерии оценки
Самоконтроль его основные методы, показатели и критерии оценки Анри Мари Раймон де Тулуз – Лотрек Монфа.Автор: Кушкова Екатеринастудентка 5 курсаспециальности этнокультурология
Анри Мари Раймон де Тулуз – Лотрек Монфа.Автор: Кушкова Екатеринастудентка 5 курсаспециальности этнокультурология Организация и методика проведения комплексных занятий
Организация и методика проведения комплексных занятий 9.2. 9А Сложное предложение и ССП начало — сокр.вар
9.2. 9А Сложное предложение и ССП начало — сокр.вар Презентация на тему Энергия ветра
Презентация на тему Энергия ветра Что такое Космос ?
Что такое Космос ? Мини-пекарня Смак. Бизнес-план
Мини-пекарня Смак. Бизнес-план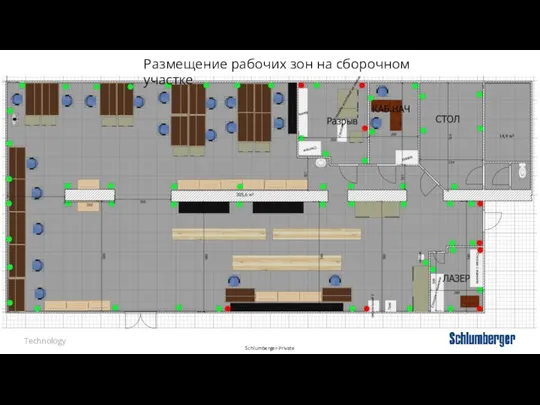 План сборочного участка
План сборочного участка Рождественский ангелочек из бисера
Рождественский ангелочек из бисера Презентация на тему Давление. Единицы давления
Презентация на тему Давление. Единицы давления  Химия и сельское хозяйство
Химия и сельское хозяйство Акция:«Пожары в природе – бедствие в народе!»15 апреля 2011 г.
Акция:«Пожары в природе – бедствие в народе!»15 апреля 2011 г. Психология китайцев
Психология китайцев История физики в вопросах и задачах
История физики в вопросах и задачах