Содержание
- 2. Элементы интегрального исчисления 1.Определение определенного интеграла 2.Основные свойства определенного интеграла 3.Формула Ньютона-Лейбница 4.Методы интегрирования 5.Геометрические приложения
- 3. Определенный интеграл, его свойства и вычисление
- 4. Понятие определенного интеграла Рассмотрим функцию y=f(x), непрерывную и ограниченную на отрезке [a,b]. Разобьем [a,b] на n
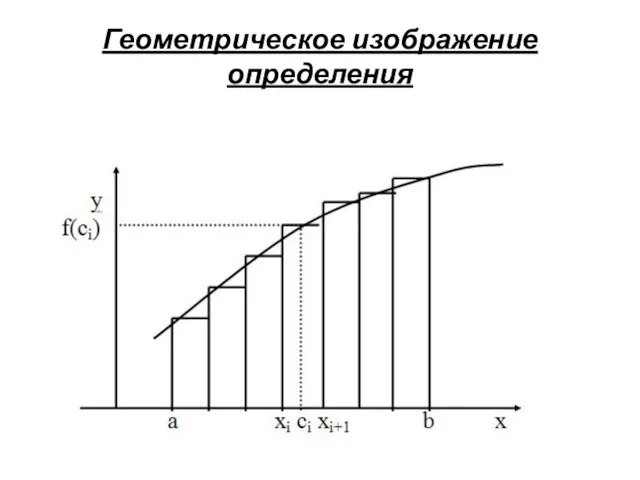
- 5. Геометрическое изображение определения
- 6. Определение интегральной суммы Интегральной суммой для функции y=f(x) на отрезке [a,b] называется сумма произведений длин элементарных
- 7. Определение определенного интеграла Определенным интегралом от функции f(x) на отрезке [a,b] называется предел (если он существует)
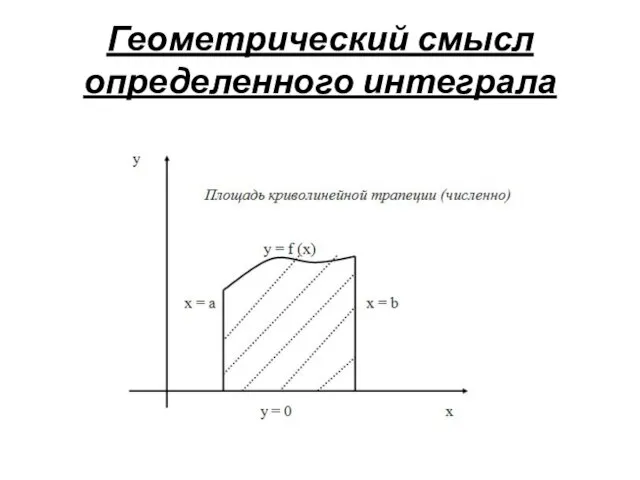
- 8. Геометрический смысл определенного интеграла
- 9. Основные свойства определенного интеграла 10 Величина определенного интеграла не зависит от обозначения переменной интегрирования (инвариантность): 20
- 10. Основные свойства определенного интеграла 30 Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то
- 11. Основные свойства определенного интеграла 40 Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой
- 12. Основные свойства определенного интеграла 50. Если подынтегральная функция f(x) на отрезке интегрирования сохраняет постоянный знак, то
- 13. Основные свойства определенного интеграла 70. Определенный интеграл от непрерывной функции равен произведению значения этой функции в
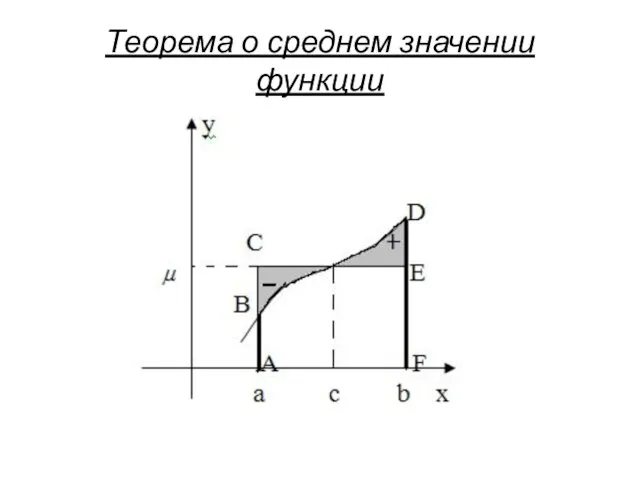
- 14. Теорема о среднем значении функции
- 15. Формула Ньютона-Лейбница. Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов интегрирования.
- 16. Методы интегрирования
- 17. Непосредственное интегрирование Этот способ основан на использовании свойств определенного интеграла, приведении подынтегрального выражения к табличной форме
- 18. Замена переменной Вычислить .
- 19. Интегрирование по частям Вычислить .
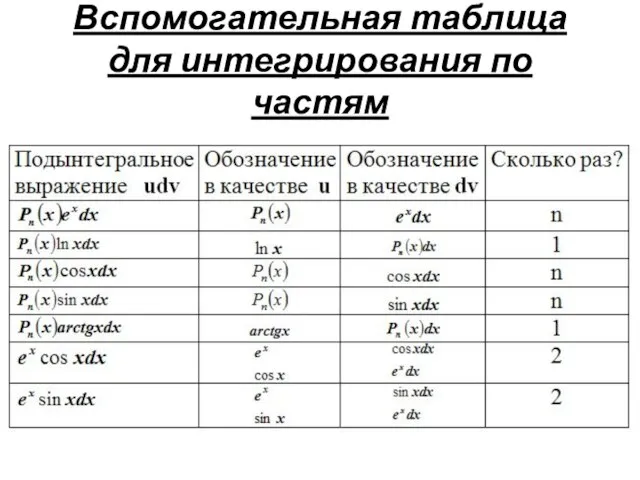
- 20. Вспомогательная таблица для интегрирования по частям
- 22. Скачать презентацию


![Понятие определенного интеграла Рассмотрим функцию y=f(x), непрерывную и ограниченную на отрезке [a,b].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/365722/slide-3.jpg)
![Определение интегральной суммы Интегральной суммой для функции y=f(x) на отрезке [a,b] называется](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/365722/slide-5.jpg)
![Определение определенного интеграла Определенным интегралом от функции f(x) на отрезке [a,b] называется](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/365722/slide-6.jpg)

![Основные свойства определенного интеграла 30 Если промежуток интегрирования [a,b] разбит на конечное](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/365722/slide-9.jpg)








 MadameTussaud’s Музей Восковых фигур Мадам Тюссо
MadameTussaud’s Музей Восковых фигур Мадам Тюссо Место учебного исследования в программе Intel «Обучение для будущего»
Место учебного исследования в программе Intel «Обучение для будущего» Потребительские кредиты
Потребительские кредиты Организация пастбищного содержания животных
Организация пастбищного содержания животных А
А Структура ВС РФ
Структура ВС РФ Северная Америка
Северная Америка «Как продолжается детство»
«Как продолжается детство» Молодые менеджеры и предприниматели Кубани
Молодые менеджеры и предприниматели Кубани Презентация на тему Углекислый газ СО2
Презентация на тему Углекислый газ СО2  Солнце воздух и вода – наши лучшие друзья
Солнце воздух и вода – наши лучшие друзья Лапта. История развития
Лапта. История развития Что такое система LanDrive ? LanDrive – это универсальная система управления по витой паре. Предназначена для автоматического и централиз
Что такое система LanDrive ? LanDrive – это универсальная система управления по витой паре. Предназначена для автоматического и централиз Презентация на тему Экологические кризисы и экологические катастрофы
Презентация на тему Экологические кризисы и экологические катастрофы История Громова Процессы на постсоветском пространстве
История Громова Процессы на постсоветском пространстве Шамшур
Шамшур Приобщение дошкольников к народной культуре в разных видах музыкальной деятельности»
Приобщение дошкольников к народной культуре в разных видах музыкальной деятельности» Тема урока
Тема урока Понятие о причастном обороте. Знаки препинания в предложениях с причастными оборотами. 6 класс
Понятие о причастном обороте. Знаки препинания в предложениях с причастными оборотами. 6 класс Презентация на тему Свет и его законы
Презентация на тему Свет и его законы  Презентация "Николай I и его портреты в изобразительном искусстве" - скачать презентации по МХК
Презентация "Николай I и его портреты в изобразительном искусстве" - скачать презентации по МХК Art City. Подбор квартиры
Art City. Подбор квартиры Фалсафа - 5
Фалсафа - 5 врол
врол Бабаево – взгляд с любовью (городской путеводитель)
Бабаево – взгляд с любовью (городской путеводитель) Бесприборные тесты для подтверждения ВИЧ-Инфекции
Бесприборные тесты для подтверждения ВИЧ-Инфекции Техника безопасностииорганизация рабочего места
Техника безопасностииорганизация рабочего места Конспект урока по окружающему миру (история)с использованием информационно-коммуникационных технологий (3 класс, программа 1-4).
Конспект урока по окружающему миру (история)с использованием информационно-коммуникационных технологий (3 класс, программа 1-4).