Неопределенный интеграл

Элементы интегрального исчисления
1.Первообразная и неопределенный интеграл
2.Основные приемы вычисления неопределенных интегралов
3.Интегрирование функций, содержащих квадратный трехчлен
4.Интегрирование дробно-рациональных функций
5.Интегрирование тригонометрических функций
6.Интегрирование некоторых иррациональностей

Неопределенный интеграл, его свойства и вычисление

Первообразная и неопределенный интеграл

Первообразная и неопределенный интеграл

Первообразная и неопределенный интеграл

Первообразная и неопределенный интеграл

Геометрический смысл неопределенного интеграла

Свойства интеграла, вытекающие из определения
Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал- подынтегральному выражению. Действительно:

Свойства интеграла, вытекающие из определения
Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянной:
3.
так как является первообразной для

Свойства интеграла

Таблица неопределенных интегралов

Таблица неопределенных интегралов

Использование свойств дифференциала
При интегрировании удобно пользоваться свойствами:

Примеры

Примеры

Интеграл от сложной функции, аргумент которой является линейной функцией

Пример

Методы интегрирования

Непосредственное интегрирование
Используя свойства неопределенного интеграла и формулы школьного курса, приводят подынтегральную функцию к табличному виду.

Замена переменной

Интегрирование по частям

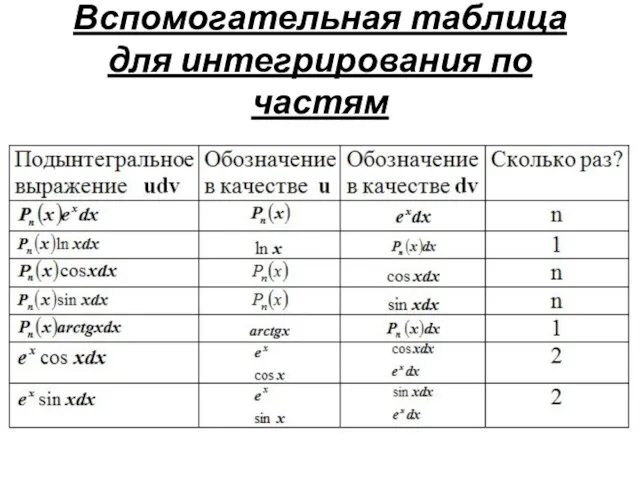
Вспомогательная таблица для интегрирования по частям

Примеры