Оптические спектры твердых тел

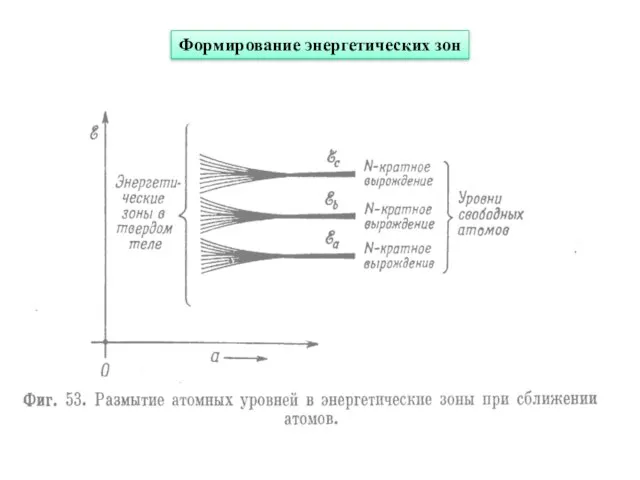
Формирование энергетических зон

Заполнение разрешенных зон электронами в твердом теле происходит последовательно в порядке возрастания энергетических уровней в зонах. Согласно принципу Паули для твердого тела, содержащего N атомов, в каждой энергетической зоне могут находиться 2N электронов. Вероятность заполнения уровня с энергией E определяется соотношением Ферми-Дирака:
f = 1/{1 + ехр[(E — EF)/kT]},
где k-константа Больцмана, EF - уровень Ферми (энергетический уровень, вероятность заполнения которого при Т = 0 К равна 0,5). Изоэнергетическая поверхность, соответствующая ЕF, называется Ферми-поверхностью. В зависимости от числа валентных электронов верхняя из заполненных зон (валентная зона) может быть занята полностью или частично. Степень заполнения валентной зоны электронами играет важную роль в формировании электрических свойств твердого тела, так как электроны заполненной полностью зоны не переносят ток.
Заполнение зон

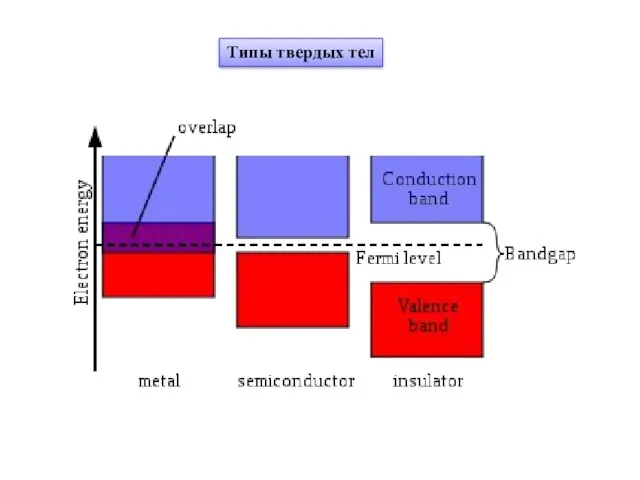
Типы твердых тел

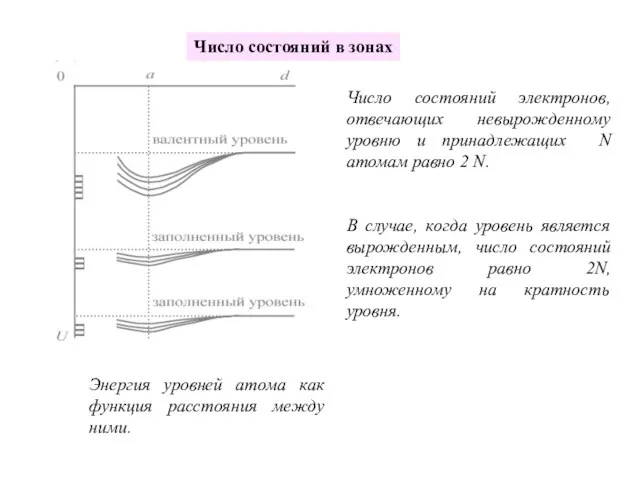
Энергия уровней атома как функция расстояния между ними.
Число состояний электронов, отвечающих невырожденному уровню и принадлежащих N атомам равно 2 N.
В случае, когда уровень является вырожденным, число состояний электронов равно 2N, умноженному на кратность уровня.
Число состояний в зонах

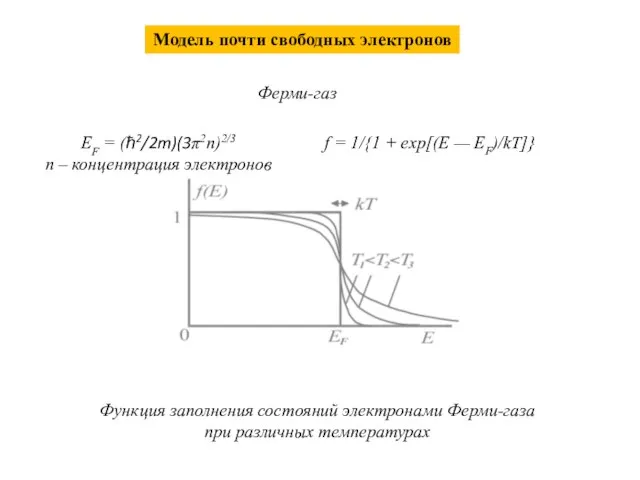
Модель почти свободных электронов
Функция заполнения состояний электронами Ферми-газа при различных температурах
EF = (ħ2/2m)(3π2n)2/3
n – концентрация электронов
f = 1/{1 + ехр[(E — EF)/kT]}
Ферми-газ

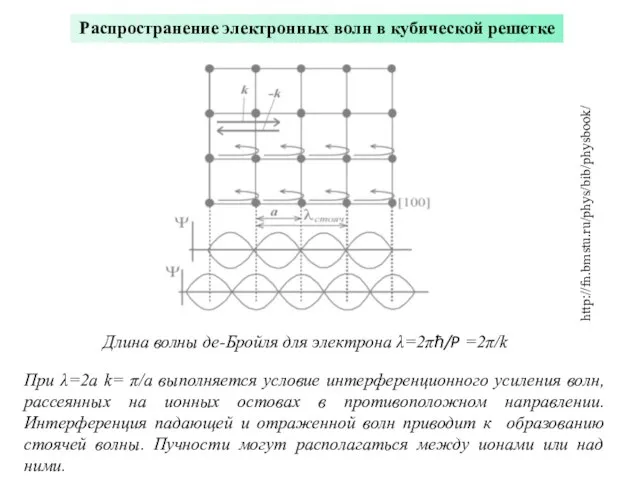
Распространение электронных волн в кубической решетке
Длина волны де-Бройля для электрона λ=2πħ/P =2π/k
При λ=2a k= π/a выполняется условие интерференционного усиления волн, рассеянных на ионных остовах в противоположном направлении. Интерференция падающей и отраженной волн приводит к образованию стоячей волны. Пучности могут располагаться между ионами или над ними.
http://fn.bmstu.ru/phys/bib/physbook/

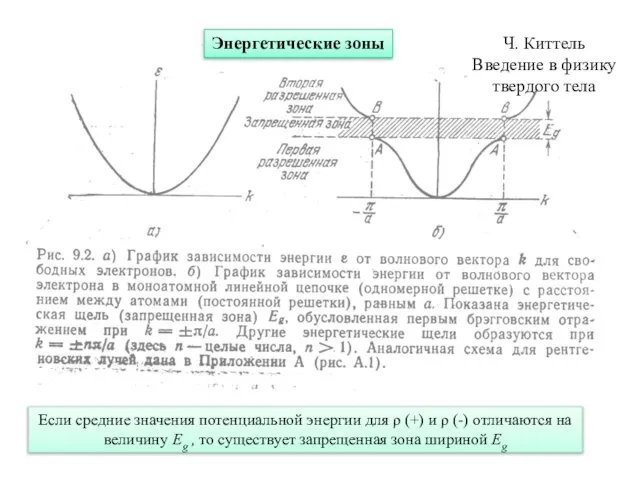
Происхождение энергетической щели
Ч. Киттель
Введение в физику
твердого тела

Энергетические зоны
Если средние значения потенциальной энергии для ρ (+) и ρ (-) отличаются на величину Eg , то существует запрещенная зона шириной Eg
Ч. Киттель
Введение в физику
твердого тела

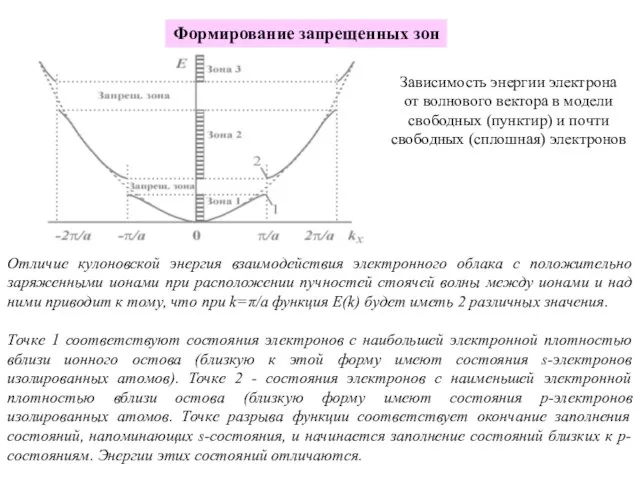
Отличие кулоновской энергия взаимодействия электронного облака с положительно заряженными ионами при расположении пучностей стоячей волны между ионами и над ними приводит к тому, что при k=π/a функция E(k) будет иметь 2 различных значения.
Точке 1 соответствуют состояния электронов с наибольшей электронной плотностью вблизи ионного остова (близкую к этой форму имеют состояния s-электронов изолированных атомов). Точке 2 - состояния электронов с наименьшей электронной плотностью вблизи остова (близкую форму имеют состояния p-электронов изолированных атомов. Точке разрыва функции соответствует окончание заполнения состояний, напоминающих s-состояния, и начинается заполнение состояний близких к p- состояниям. Энергии этих состояний отличаются.
Формирование запрещенных зон
Зависимость энергии электрона
от волнового вектора в модели
свободных (пунктир) и почти
свободных (сплошная) электронов

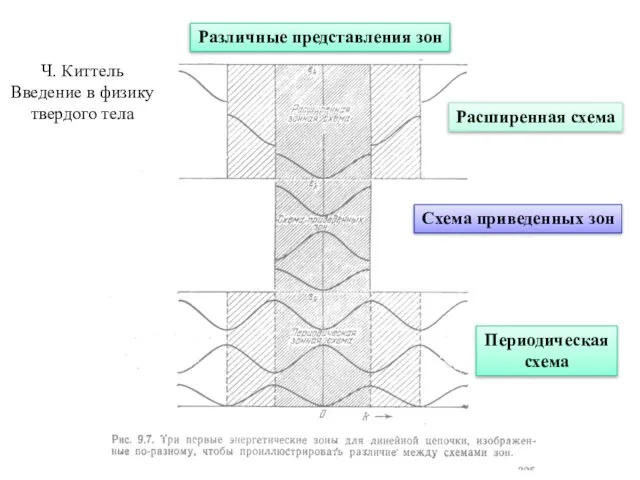
Различные представления зон
Периодическая схема
Схема приведенных зон
Расширенная схема
Ч. Киттель
Введение в физику
твердого тела

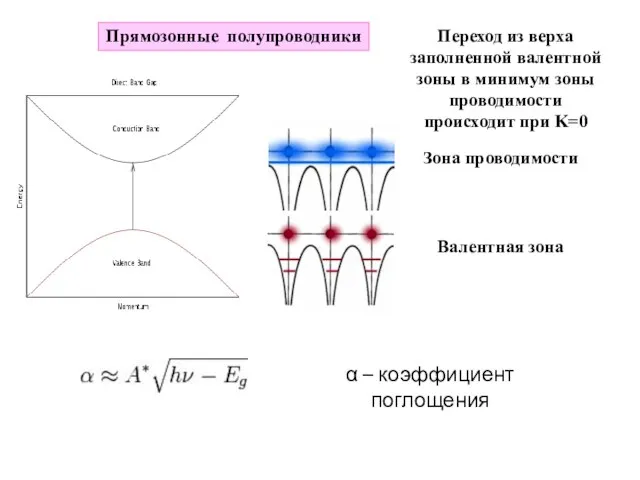
Прямозонные полупроводники
Переход из верха заполненной валентной зоны в минимум зоны проводимости происходит при K=0
Зона проводимости
Валентная зона
,
α – коэффициент поглощения

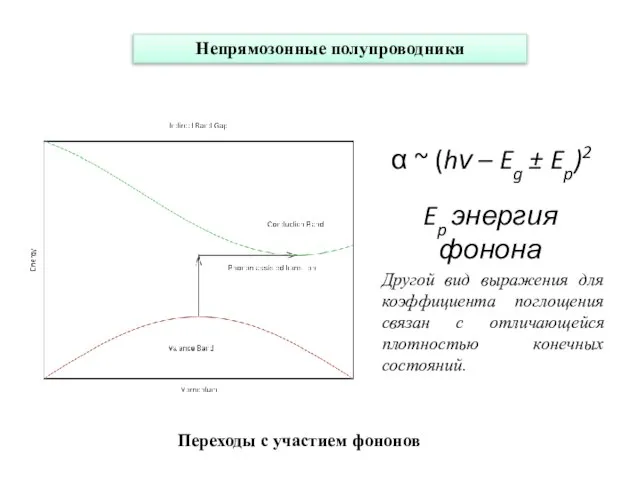
Непрямозонные полупроводники
α ~ (hν – Eg ± Ep)2
Ep энергия фонона
Переходы с участием фононов
Другой вид выражения для коэффициента поглощения связан с отличающейся плотностью конечных состояний.

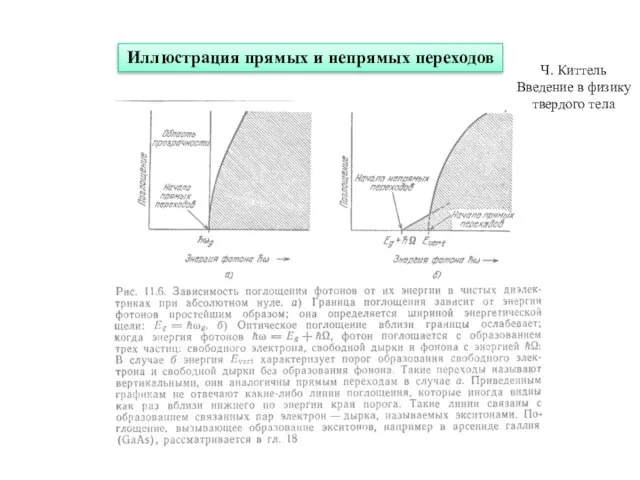
Иллюстрация прямых и непрямых переходов
Ч. Киттель
Введение в физику
твердого тела

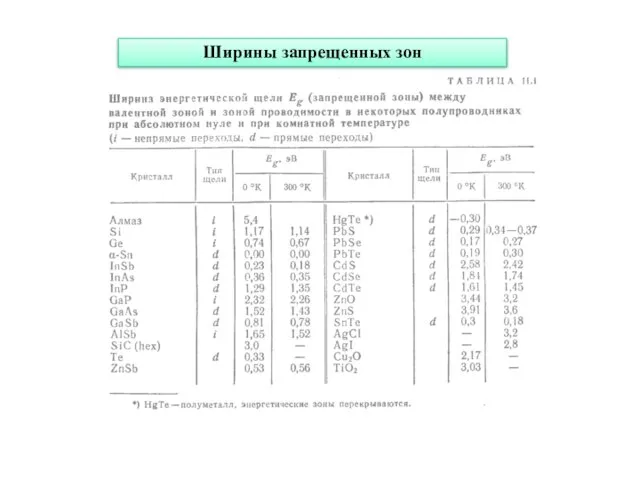
Ширины запрещенных зон

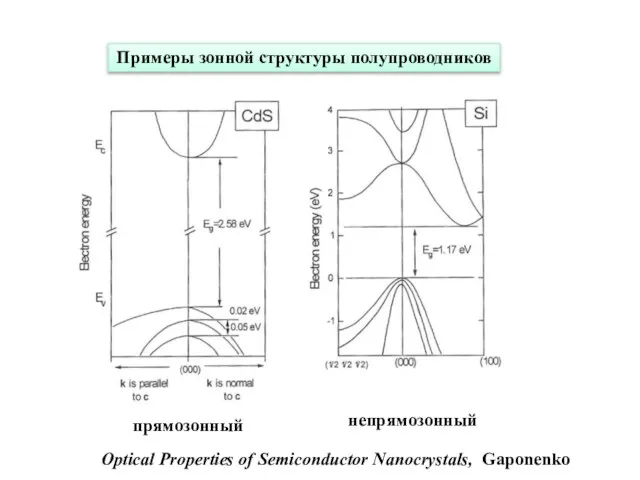
Optical Properties of Semiconductor Nanocrystals, Gaponenko
Примеры зонной структуры полупроводников
прямозонный
непрямозонный

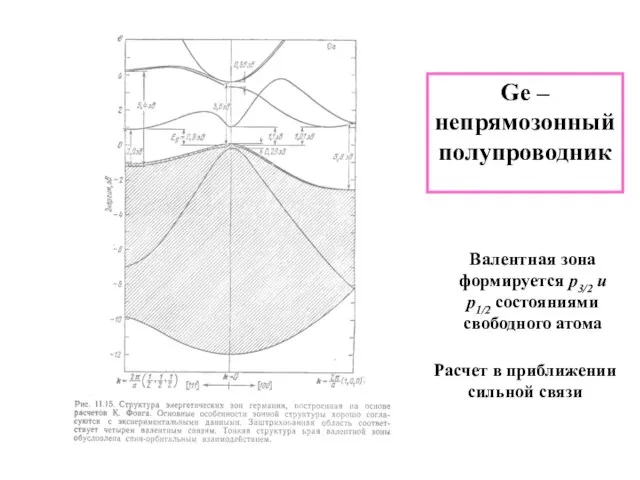
Ge –
непрямозонный
полупроводник
Валентная зона формируется p3/2 и p1/2 состояниями свободного атома
Расчет в приближении сильной связи

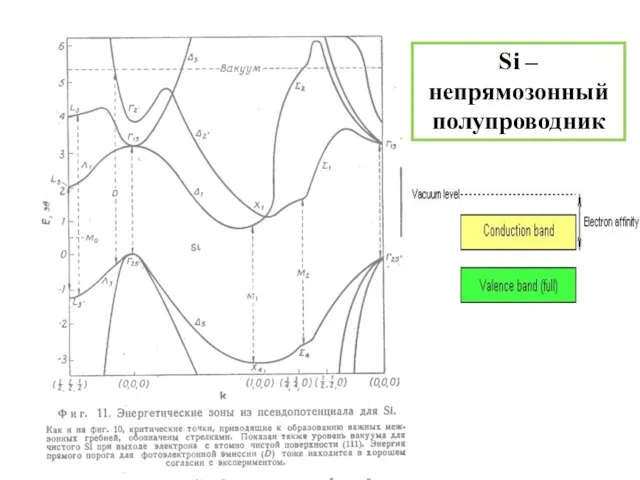
Si – непрямозонный полупроводник

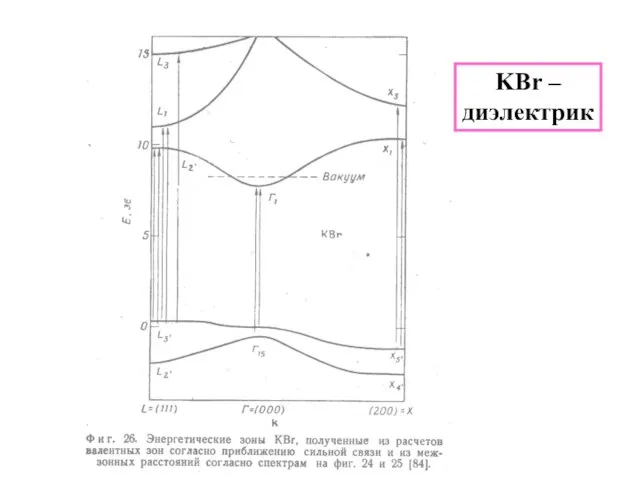
KBr –
диэлектрик

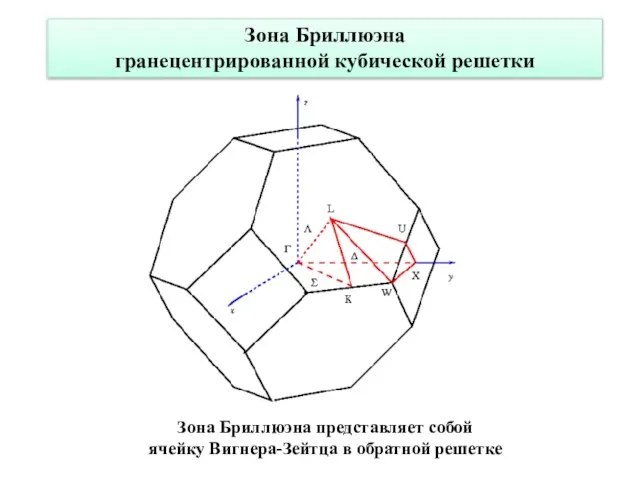
Зона Бриллюэна
гранецентрированной кубической решетки
Зона Бриллюэна представляет собой
ячейку Вигнера-Зейтца в обратной решетке

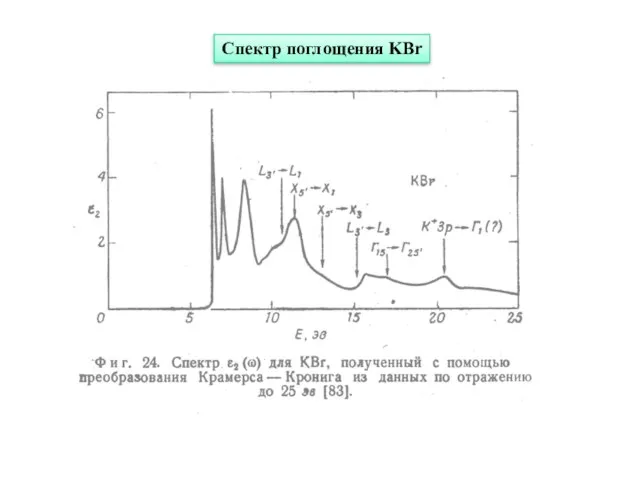
Спектр поглощения KBr

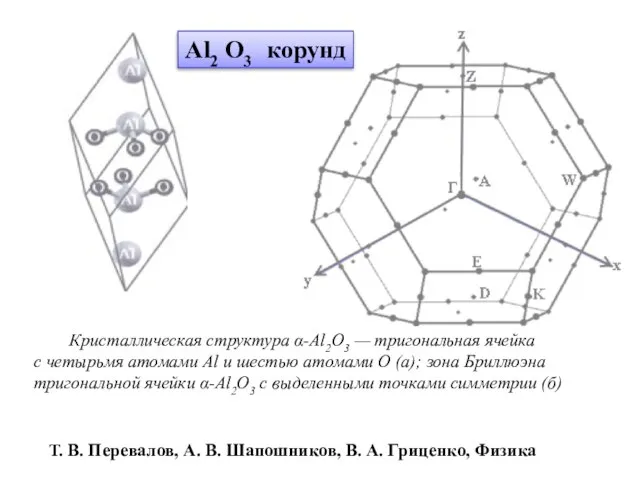
Т. В. Перевалов, А. В. Шапошников, В. А. Гриценко, Физика
Al2 O3 корунд
Кристаллическая структура α-Al2O3 — тригональная ячейка
с четырьмя атомами Al и шестью атомами O (а); зона Бриллюэна тригональной ячейки α-Al2O3 с выделенными точками симметрии (б)

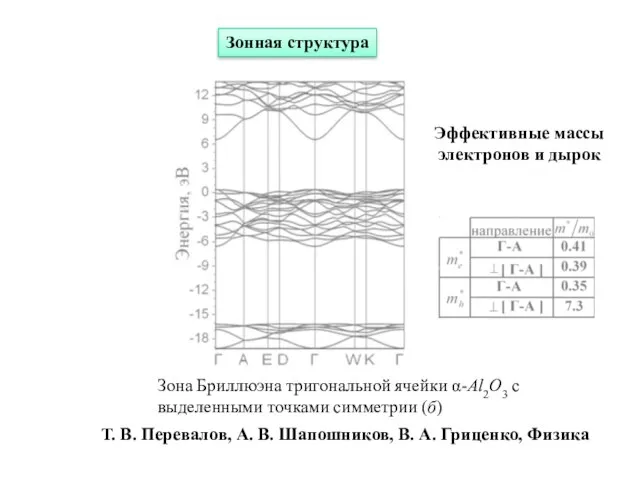
Зона Бриллюэна тригональной ячейки α-Al2O3 с выделенными точками симметрии (б)
Т. В. Перевалов, А. В. Шапошников, В. А. Гриценко, Физика
Зонная структура
Эффективные массы электронов и дырок

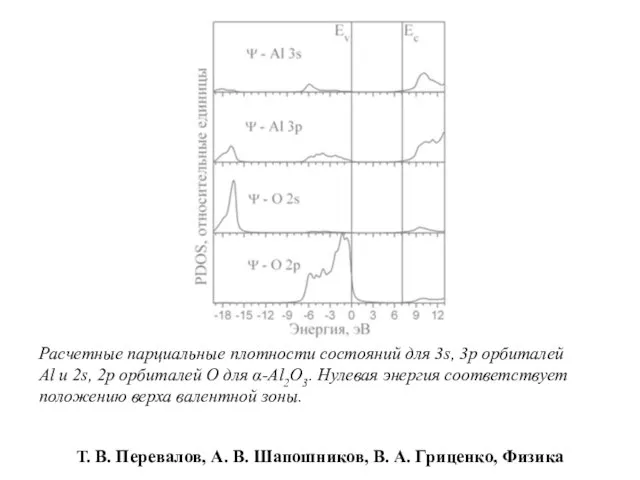
Расчетные парциальные плотности состояний для 3s, 3p орбиталей Al и 2s, 2p орбиталей O для α-Al2O3. Нулевая энергия соответствует положению верха валентной зоны.
Т. В. Перевалов, А. В. Шапошников, В. А. Гриценко, Физика

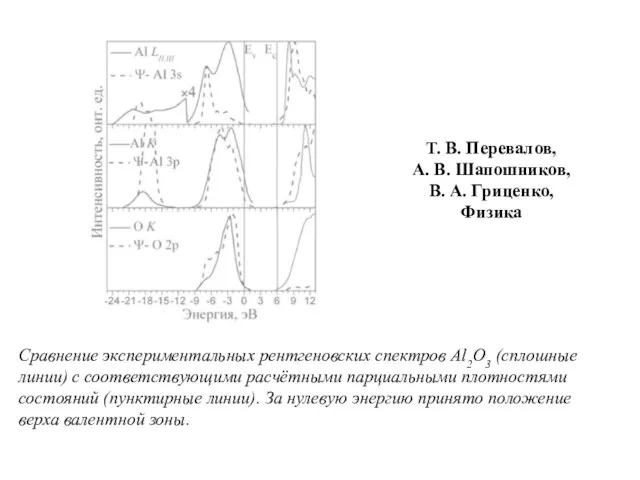
Сравнение экспериментальных рентгеновских спектров Al2O3 (сплошные линии) с соответствующими расчётными парциальными плотностями состояний (пунктирные линии). За нулевую энергию принято положение верха валентной зоны.
Т. В. Перевалов,
А. В. Шапошников,
В. А. Гриценко,
Физика

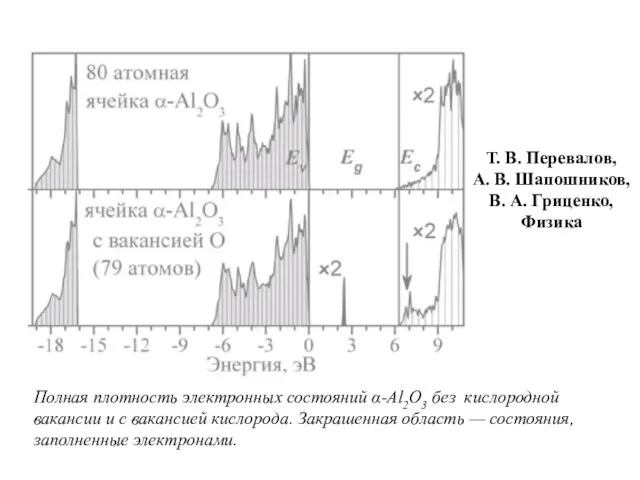
Полная плотность электронных состояний α-Al2O3 без кислородной вакансии и с вакансией кислорода. Закрашенная область — состояния, заполненные электронами.
Т. В. Перевалов,
А. В. Шапошников,
В. А. Гриценко,
Физика

Положение дефектного уровня ниже дна зоны проводимости на 0,5 эВ, из чего следует, что вакансия кислорода является центром локализации
для электронов.
Дефектный уровень лежит выше потолка валентной зоны на 2,9 эВ. Вследствие этого вакансия кислорода в α-Al2O3 является центром локализации также для дырок.
Пространственное распределение: а — отрицательного заряда электрона и б — положительного заряда дырки в 79 атомной ячейке α-Al2O3 с вакансией кислорода.
Серые области соответствуют
поверхностям одинакового отрица-
тельного/положительного заряда
Т. В. Перевалов, А. В. Шапошников, В. А. Гриценко, Физика
а
б

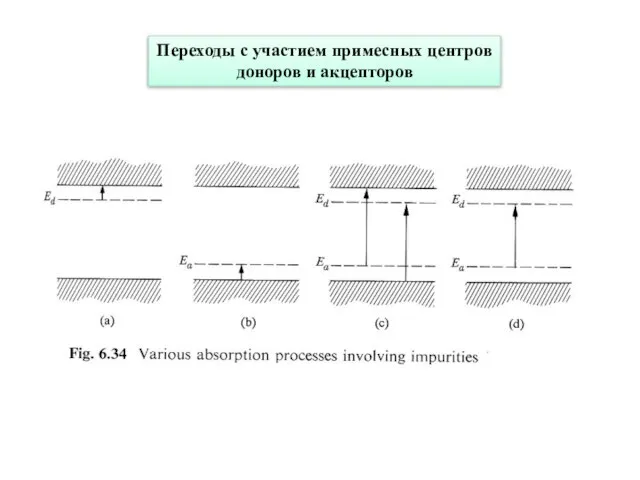
Переходы с участием примесных центров
доноров и акцепторов

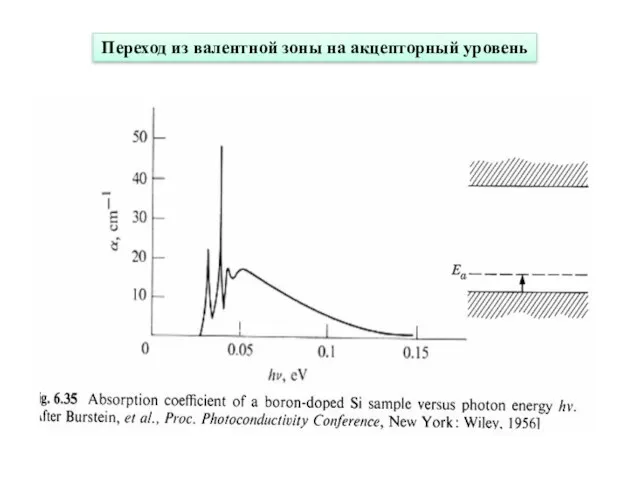
Переход из валентной зоны на акцепторный уровень

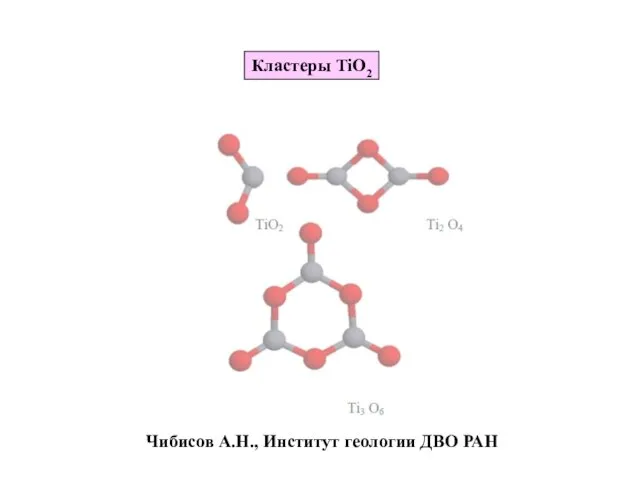
Чибисов А.Н., Институт геологии ДВО РАН
Кластеры TiO2

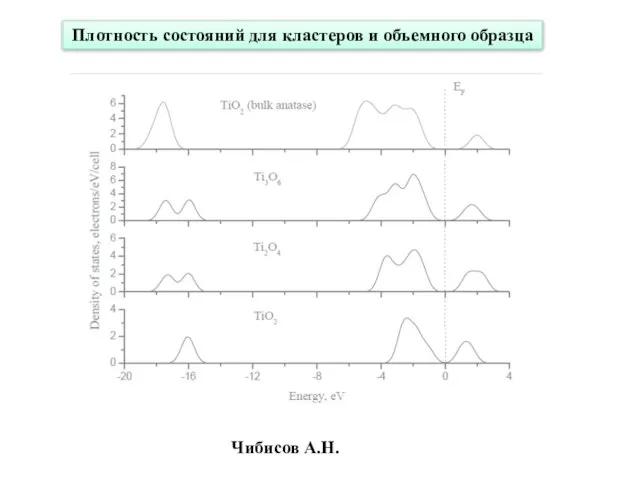
Плотность состояний для кластеров и объемного образца
Чибисов А.Н.

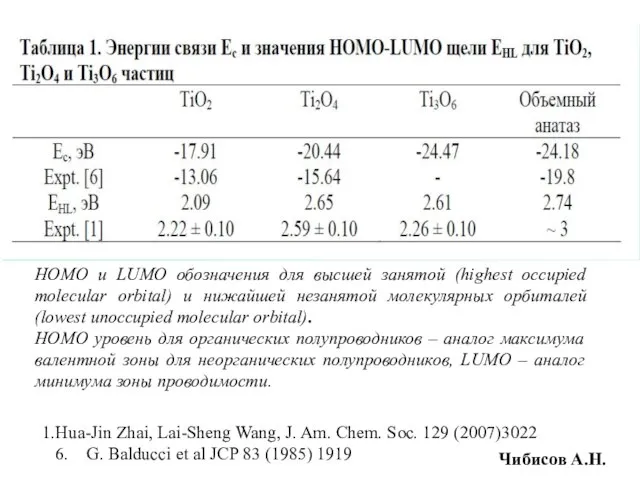
Hua-Jin Zhai, Lai-Sheng Wang, J. Am. Chem. Soc. 129 (2007)3022
6. G. Balducci et al JCP 83 (1985) 1919
Чибисов А.Н.
HOMO и LUMO обозначения для высшей занятой (highest occupied molecular orbital) и нижайшей незанятой молекулярных орбиталей (lowest unoccupied molecular orbital).
HOMO уровень для органических полупроводников – аналог максимума валентной зоны для неорганических полупроводников, LUMO – аналог минимума зоны проводимости.