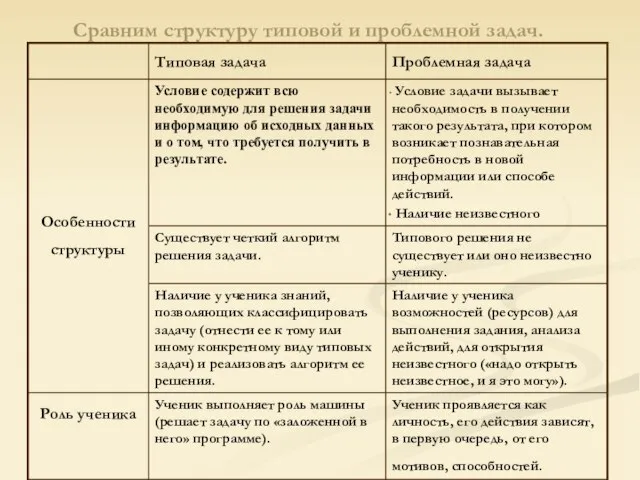
Слайд 2Сравним структуру типовой и проблемной задач.
Слайд 3Пример:
Задача № 1.
Исследуйте, как влияет на график изменение одного из коэффициентов а,b,с

в уравнении параболы y = ax + bx + c. Для этого в одной системе координат начертите параболы:
y = x - 4x + c для с = 0; 1; 2; 4 и с = -1; -2;
y = x + bx + 4 для b = 0; 1; 4; 5 и b = -1; -4; -5;
y = ax + 4x + 5 для а = 0,5; 1; 2; 4.
Сделать выводы.
Слайд 4Исследование:
y= x - 4x+c
y
x
2
-4
0
C=1
C=0
1
C=2
-2
C=4
C=-2
-6
Ось симметрии x=0
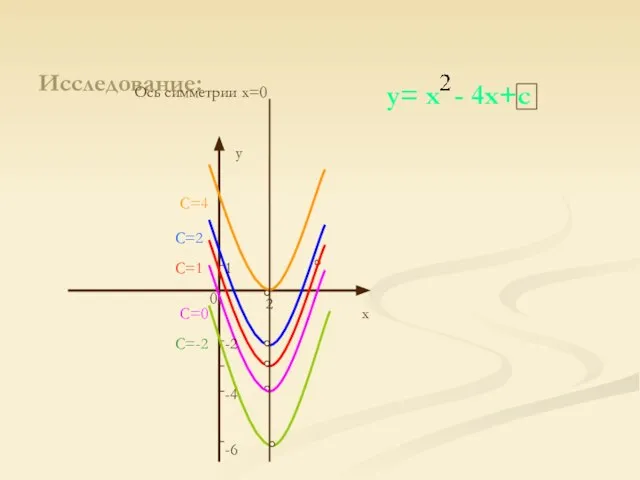
Слайд 5Выводы:
Вершины всех парабол лежат на одной и той же вертикальной прямой (х=2).

При увеличении с парабола сдвигается вдоль этой вертикали вверх, а при уменьшении – вниз. (Все параболы «равны» между собой, так как коэффициент а один и тот же.)
Слайд 6Исследование:
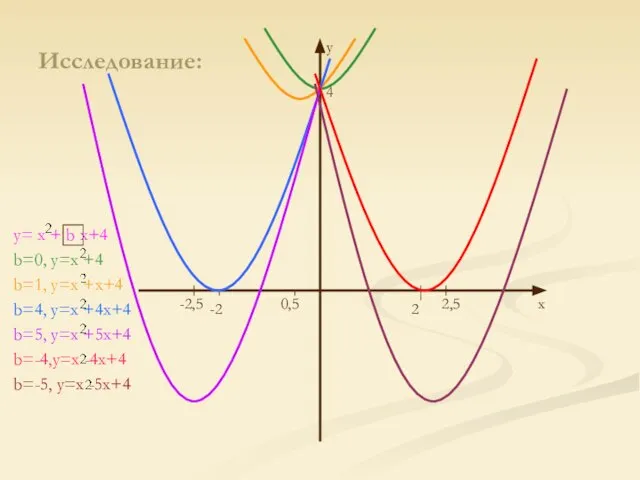
y= x + b x+4
b=0, y=x +4
b=1, y=x +x+4
b=4, y=x +4x+4
b=5, y=x
+5x+4
b=-4,y=x -4x+4
b=-5, y=x -5x+4
4
y
x
0,5
-2
-2,5
2
2,5
Слайд 7Выводы:
При b =0 имеем формулу y=x²+4, т.е параболу, симметричную относительно оси y;

ее вершина – точка (0;4). С изменением b вершины парабол смещаются (однако все графики проходят через точку (0;4)). Если b – число положительное, то с увеличением b вершина смещается влево и вниз; если b – число отрицательное, то с увеличением |b| вершина смещается вправо и вниз. (Все параболы «равны» между собой, так как коэффициент при х² один и тот же.)
Слайд 8Исследование:
y=a x +4x+5
a=0,5, y=0,5x +4x+5
a=1, y=x +4x+5
a=2, y=x +4x+5
a=4, y=4x +4x+5
y
x
-3
-4
5
-1
-2
3
4
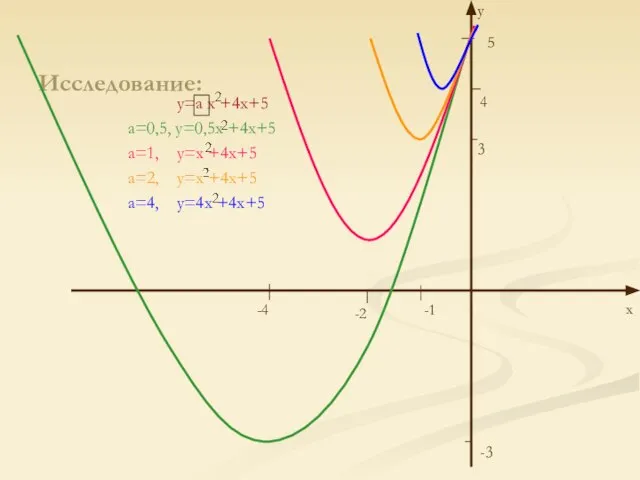
Слайд 9Выводы:
Так как предлагается провести наблюдение для положительных значений a, то и вывод

будет сделан лишь для a>0. При увеличении a меняется форма параболы; она становится «круче». Вершины парабол перемещаются вправо и вверх, оставаясь при этом левее оси y и ниже прямой y=-5
Слайд 10Задача №2.
На рисунке изображен график функции у = ах2 + bх +
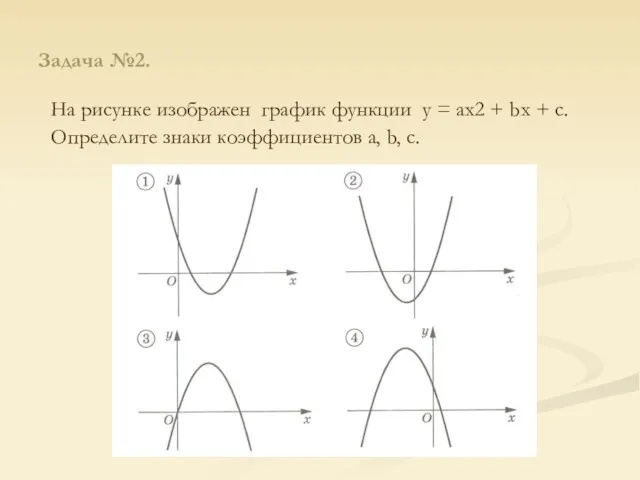
с. Определите знаки коэффициентов а, b, с.
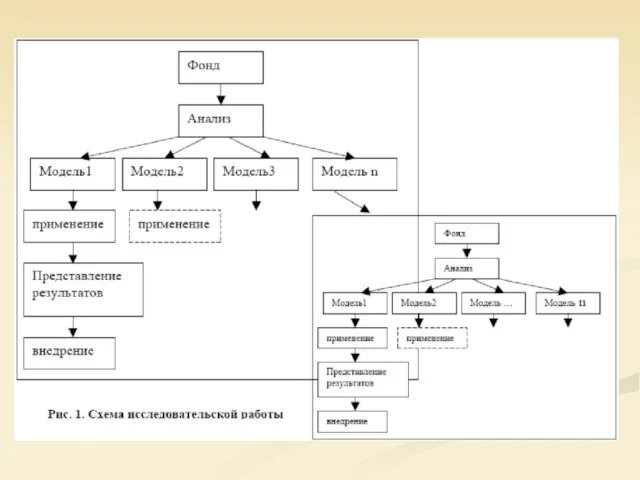
Слайд 11Структура исследовательской работы отражена на рис. 1.
Изучение объекта в математике целесообразно

вести в такой последовательности (Белова Г.В., 2003):
определение;
элементы (основные и дополнительные);
свойства;
признаки (в математике признак - это необходимые и достаточные условия существования объекта);
применение.
Параллельно идет освоение различных этапов учебной исследовательской работы:
сбора информационного фонда;
его анализа;
построения и применения моделей,
представления и внедрения результатов исследования.










 Работы МДК. Шрифты
Работы МДК. Шрифты Начало Первой мировой войны. Роль Восточного фронта в войне
Начало Первой мировой войны. Роль Восточного фронта в войне План експерименту на тему: Дослідження ролі відчуттів у пізнавальній діяльності людини
План експерименту на тему: Дослідження ролі відчуттів у пізнавальній діяльності людини Контроль как один из методов диагностики учебных достижений учащихся в школьном курсе химии
Контроль как один из методов диагностики учебных достижений учащихся в школьном курсе химии В. Г . Короленко - прозаик, публицист, общественный деятель
В. Г . Короленко - прозаик, публицист, общественный деятель Коммуна Сен-Дени прилегает к Парижу и входит в состав первого надмуниципального агломерационного объединения в Иль-де-Франс
Коммуна Сен-Дени прилегает к Парижу и входит в состав первого надмуниципального агломерационного объединения в Иль-де-Франс Международная классификация многоствольных скважин TAML
Международная классификация многоствольных скважин TAML Презентация на тему Федор Иванович Крузенштерн и его кругосветное путешествие
Презентация на тему Федор Иванович Крузенштерн и его кругосветное путешествие Реклама на дисплеях ПРЕЗЕНТАЦИЯ
Реклама на дисплеях ПРЕЗЕНТАЦИЯ Порядок открытого отбора кандидатов на должности руководителей органов исполнительной власти. Новгородская область 2017 год
Порядок открытого отбора кандидатов на должности руководителей органов исполнительной власти. Новгородская область 2017 год Л.Андреев «Кусака» "Мы несём ответственность за тех, кого приручили» Павленко Любовь Ивановна,учитель русского языка и литератур
Л.Андреев «Кусака» "Мы несём ответственность за тех, кого приручили» Павленко Любовь Ивановна,учитель русского языка и литератур Игумен Андрей
Игумен Андрей Музеи России
Музеи России День правовой помощи детям
День правовой помощи детям Пришли Святки: гаданья да колядки
Пришли Святки: гаданья да колядки Радиоавтоматика. Лекция 14
Радиоавтоматика. Лекция 14 Царство Грибы. Грибы-паразиты
Царство Грибы. Грибы-паразиты Путешествие в мир знакомой музыки
Путешествие в мир знакомой музыки Кому нужен ВСД. Комплексная транспортная система Санкт-Петербурга
Кому нужен ВСД. Комплексная транспортная система Санкт-Петербурга Летопись независимости
Летопись независимости Эффективность рекламной кампании и показатели эффективности медиапланов
Эффективность рекламной кампании и показатели эффективности медиапланов Презентация на тему Органы дыхания человека
Презентация на тему Органы дыхания человека  Качественные методы исследований
Качественные методы исследований Огонь - друг или враг
Огонь - друг или враг Лишение (ограничение) законных представителей родительских прав
Лишение (ограничение) законных представителей родительских прав Математика в моей будущей профессии
Математика в моей будущей профессии Цветовые сочетания
Цветовые сочетания Синтаксическая роль инфинитива
Синтаксическая роль инфинитива