Основы цифровой обработки сигналов

План лекции
Основные определения
Дискретизация, теорема Котельникова
Линейные системы
Дискретное преобразование Фурье
Спектральный анализ
Фильтрация, быстрая свертка
Приложения

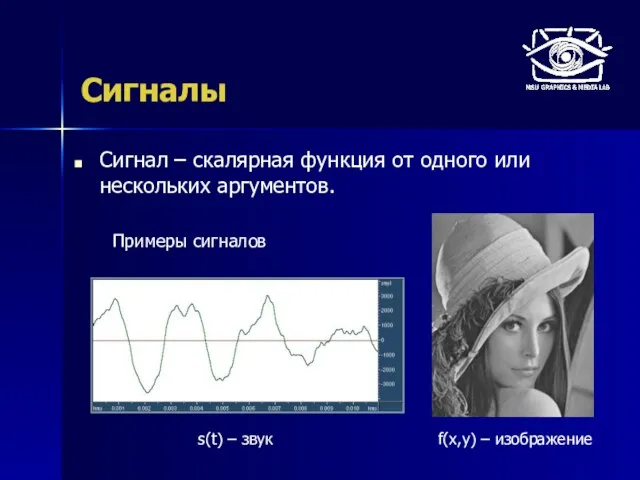
Сигналы
Сигнал – скалярная функция от одного или нескольких аргументов.
s(t) – звук
Примеры сигналов
f(x,y) – изображение

Сигналы
Аналоговые (непрерывные)
Примеры:
звук в воздухе или в проводе, идущем от микрофона
изображение (до ввода в компьютер)
запись показаний датчика
Цифровые (дискретные)
Примеры:
звук в компьютере (одномерный массив чисел)
изображение в компьютере (двумерный массив чисел)
запись показаний датчика в компьютере (одномерный массив)
Одномерный цифровой сигнал

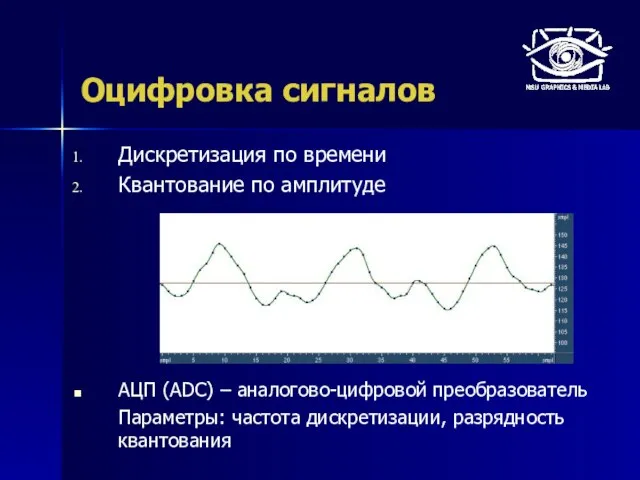
Оцифровка сигналов
Дискретизация по времени
Квантование по амплитуде
АЦП (ADC) – аналогово-цифровой преобразователь
Параметры: частота дискретизации, разрядность квантования

Оцифровка сигналов
При каких условиях по цифровому сигналу можно точно восстановить исходный аналоговый?
Предположим, что значения амплитуд в цифровом сигнале представлены точно.
Введем понятие спектра аналогового сигнала:
(разложение на синусоиды с различными частотами)
x(t) – исходный сигнал
X(ν) – спектр, т.е. коэффициенты при гармониках с частотой ν

Теорема Котельникова
Пусть
спектр сигнала x(t) не содержит частот выше F, т.е. X(ν)=0 за пределами отрезка [-F, F]
дискретизация сигнала x(t) производится с частотой Fs , т.е. в моменты времени nT, здесь T= Fs-1
Fs > 2F
Тогда исходный аналоговый сигнал x(t) можно точно восстановить из его цифровых отсчетов x(nT), пользуясь интерполяционной формулой

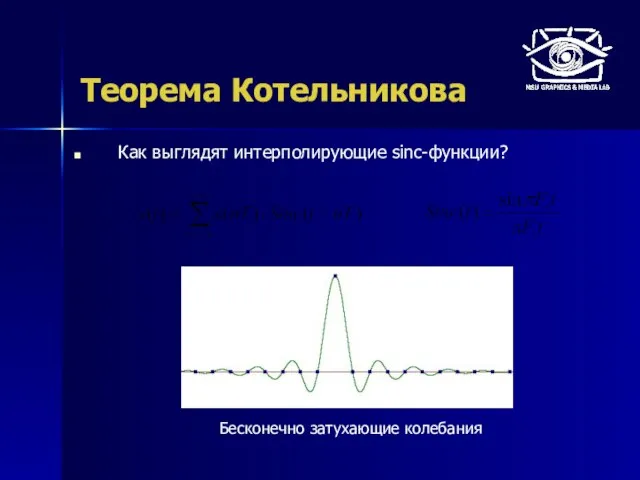
Теорема Котельникова
Как выглядят интерполирующие sinc-функции?
Бесконечно затухающие колебания

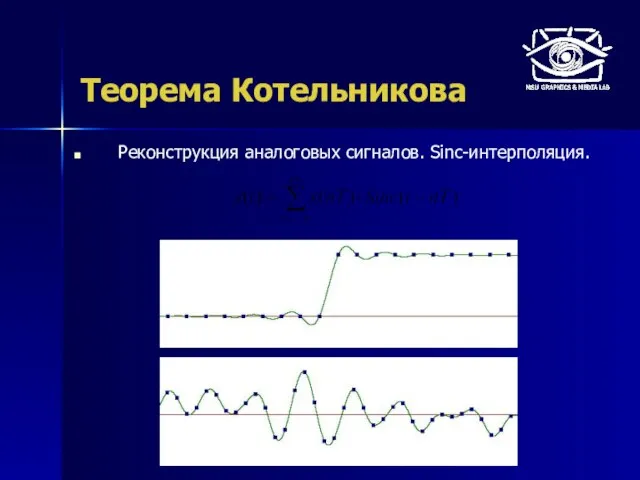
Теорема Котельникова
Реконструкция аналоговых сигналов. Sinc-интерполяция.

Эффект Гиббса
Применимость sinc-интерполяции для изображений
Эффект Гиббса: пульсации сигнала при ограничении его спектра
Цифровые отсчеты
sinc-интерполяция
другая интерполяция

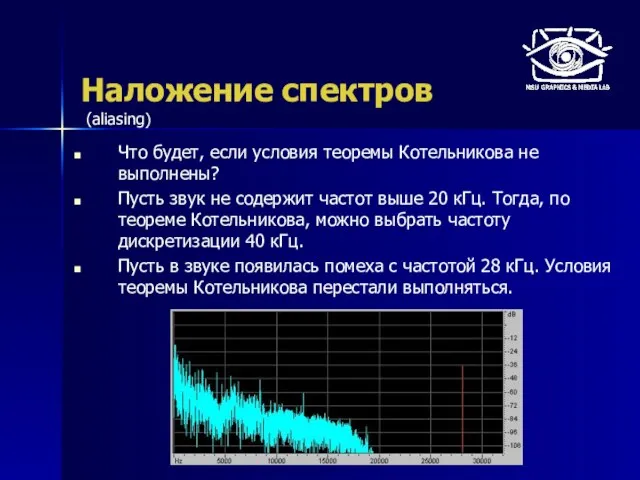
Наложение спектров
Что будет, если условия теоремы Котельникова не выполнены?
Пусть звук не содержит частот выше 20 кГц. Тогда, по теореме Котельникова, можно выбрать частоту дискретизации 40 кГц.
Пусть в звуке появилась помеха с частотой 28 кГц. Условия теоремы Котельникова перестали выполняться.
(aliasing)

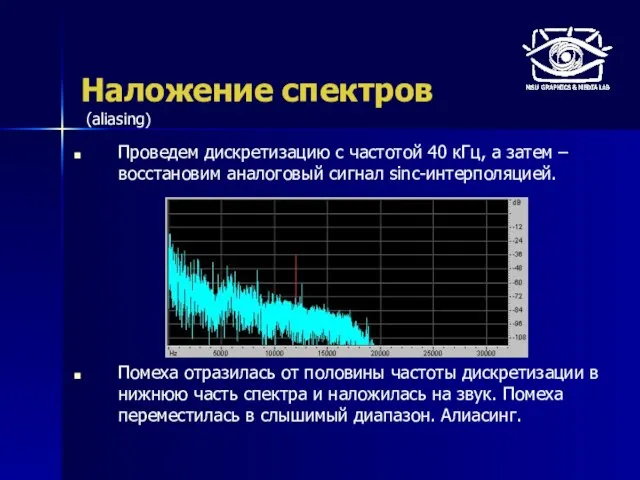
Наложение спектров
Проведем дискретизацию с частотой 40 кГц, а затем – восстановим аналоговый сигнал sinc-интерполяцией.
Помеха отразилась от половины частоты дискретизации в нижнюю часть спектра и наложилась на звук. Помеха переместилась в слышимый диапазон. Алиасинг.
(aliasing)

Наложение спектров
Как избежать наложения спектров?
Применить перед оцифровкой анти-алиасинговый фильтр
Он подавит все помехи выше половины частоты дискретизации (выше 20 кГц) и пропустит весь сигнал ниже 20 кГц.
После этого условия теоремы Котельникова будут выполняться и алиасинга не возникнет.
Следовательно, по цифровому сигналу можно будет восстановить исходный аналоговый сигнал.
(aliasing)

Линейные системы
Система – преобразователь сигнала
Линейность:
Инвариантность к сдвигу:
H
x(t)
y(t)

Импульсная характеристика
Единичный импульс δ[n]
Разложение произвольного сигнала на взвешенную сумму единичных импульсов

Импульсная характеристика
Отклик системы на единичный импульс
h[n] – импульсная характеристика системы (импульсный отклик системы)

Импульсная характеристика
Вычисление отклика линейной системы на произвольный входной сигнал
Свертка
h[n] – ядро свертки

Линейные системы
Итак, любая линейная инвариантная к сдвигу система производит операцию свертки входного сигнала со своей импульсной характеристикой.
Важное свойство линейных систем:
При подаче на любую линейную систему синусоиды, на выходе получается синусоида той же частоты, что и на входе. Измениться могут только ее амплитуда или фаза.
Следствие: линейные системы удобно анализировать, раскладывая любые входные сигналы на синусоиды.

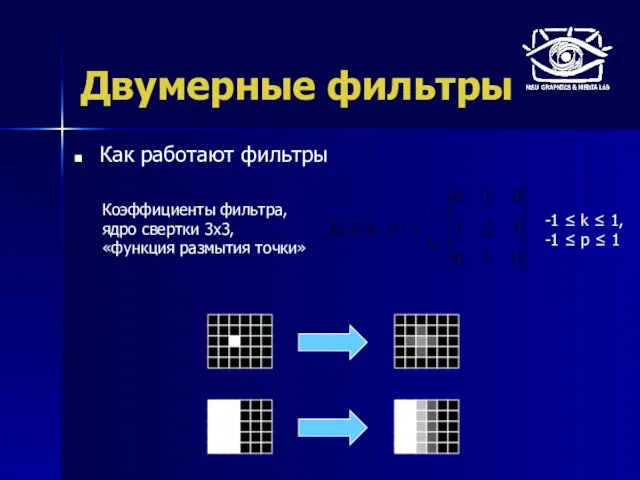
Двумерные фильтры
Как работают фильтры
Коэффициенты фильтра,
ядро свертки 3x3,
«функция размытия точки»
-1 ≤ k ≤ 1,
-1 ≤ p ≤ 1

Примеры фильтров
Простейшее размытие
Константное размытие
“box-фильтр”
(любой размер фильтра)
Гауссово размытие
(любой размер фильтра)

Примеры фильтров
Повышение резкости
Нахождение границ
Тиснение
+ модуль, нормировка, применение порога…
+ сдвиг яркости, нормировка…

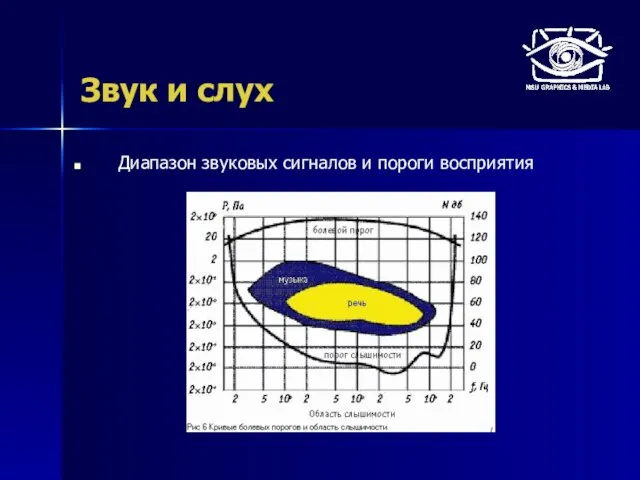
Звук и слух
Диапазон звуковых сигналов и пороги восприятия

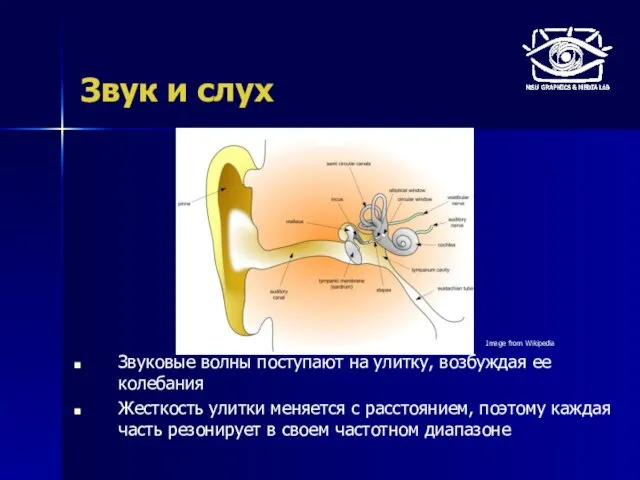
Звук и слух
Звуковые волны поступают на улитку, возбуждая ее колебания
Жесткость улитки меняется с расстоянием, поэтому каждая часть резонирует в своем частотном диапазоне
Image from Wikipedia

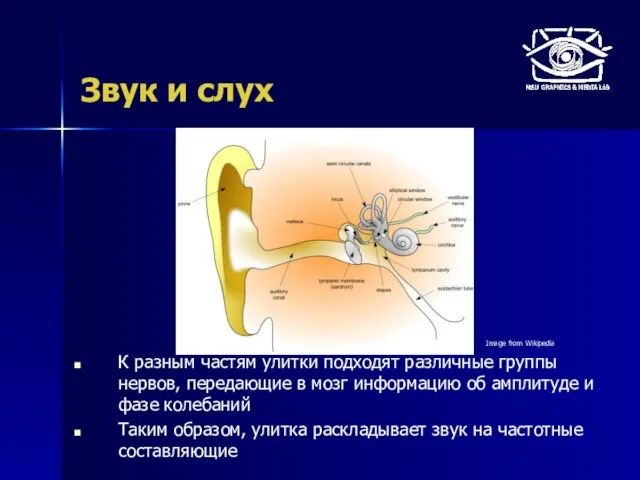
Звук и слух
К разным частям улитки подходят различные группы нервов, передающие в мозг информацию об амплитуде и фазе колебаний
Таким образом, улитка раскладывает звук на частотные составляющие
Image from Wikipedia

Преобразование Фурье
Зачем раскладывать сигналы на синусоиды?
Анализ линейных систем
Особенности слухового восприятия
Хорошо разработана теория и практика
Дискретное преобразование Фурье (ДПФ)
Для вещественного сигнала
Прямое и обратное преобразования Фурье

Преобразование Фурье
Базисные функции дискретного преобразования Фурье для сигнала длины N = 8.
Имеем N/2 + 1 = 5 различных базисных частот.
Имеем N+2 базисные функции, 2 из которых тождественно равны нулю.
Количество информации не изменяется: N чисел

Преобразование Фурье
Базисные функции образуют N-мерный ортогональный базис в пространстве N-мерных векторов исходных сигналов.
Следовательно, разложение обратимо, т.е. по коэффициентам разложения (Ak, Bk) можно точно восстановить исходный дискретный сигнал.
Обратное преобразование Фурье – вычисление суммы конечного ряда Фурье (сложить N штук N-точечных синусоид со своими коэффициентами).

Преобразование Фурье
Прямое преобразование Фурье – вычисление скалярных произведений сигнала на базисные функции:
Для вычисления всех коэффициентов по этому алгоритму требуется примерно N2 умножений: очень много при больших длинах сигнала N.

Преобразование Фурье
Быстрое преобразование Фурье (БПФ, FFT) – ускоренный алгоритм вычисления ДПФ
Основан на периодичности базисных функций (много одинаковых множителей)
Математически точен (ошибки округления даже меньше, т.к. меньше число операций)
Число умножений порядка N·log2N, намного меньше, чем N2
Ограничение: большинство реализаций FFT принимают только массивы длиной N = 2m
Существует и обратное БПФ (IFFT) – такой же быстрый алгоритм вычисления обратного ДПФ.

Преобразование Фурье
Входные данные FFT
N = 2m, размер FFT
Входной вектор длины N, иногда в комплексном представлении
Выходные данные FFT
Коэффициенты Ak и Bk, иногда записанные в комплексном представлении

Преобразование Фурье
Двумерное ДПФ
Базисные функции имеют вид двумерных синусоид с разными углами наклона и фазами
Вычисление двумерного ДПФ
Прямой способ – скалярные произведения со всеми базисными функциями. Очень много операций.
Быстрый способ – декомпозиция на одномерные ДПФ

Преобразование Фурье
Быстрое вычисление двумерного ДПФ
Вычислить одномерные комплексные ДПФ от каждой строки изображения. Результаты записать в виде комплексных массивов «обратно» в промежуточное «комплексное» изображение.
Вычислить одномерные комплексные ДПФ от каждого столбца промежуточного комплексного изображения. Комплексные результаты записать «обратно». Это и есть коэффициенты двумерного ДПФ.
Одномерные ДПФ можно считать с помощью FFT

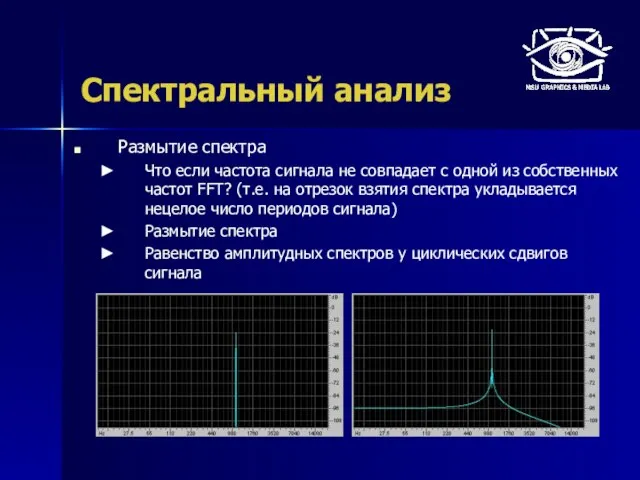
Спектральный анализ
Размытие спектра
Что если частота сигнала не совпадает с одной из собственных частот FFT? (т.е. на отрезок взятия спектра укладывается нецелое число периодов сигнала)
Размытие спектра
Равенство амплитудных спектров у циклических сдвигов сигнала

Спектральный анализ
Как вычислить и отобразить спектр сигнала?
Взять нужный отрезок сигнала длины 2m; если нужный отрезок короче – дополнить его нулями.
Если нужно – устранить из сигнала постоянную составляющую (вычесть константу – среднее значение).
Если нужно – домножить сигнал на весовое окно, плавно спадающее к краям (для уменьшения размытия спектра).
Вычислить FFT.
Перевести комплексные коэффициенты в полярную форму: получить амплитуды.
Отобразить график зависимости амплитуды от частоты.
Примеры весовых окон

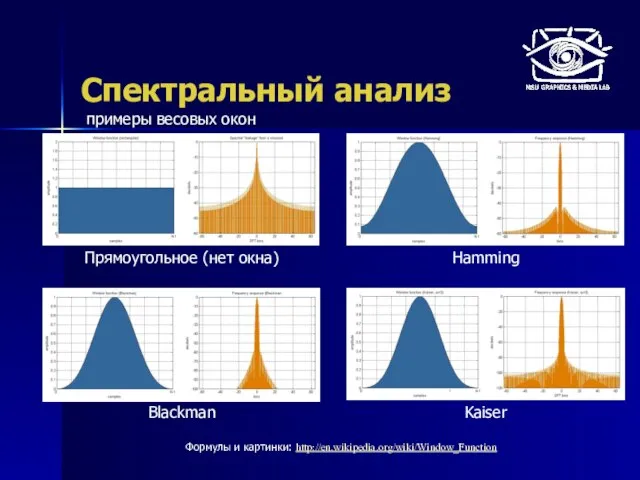
Спектральный анализ
Прямоугольное (нет окна)
Hamming
Blackman
Kaiser
Формулы и картинки: http://en.wikipedia.org/wiki/Window_Function
примеры весовых окон

Спектральный анализ
Отображение спектров изображений
Спектр – это изображение, показывающая зависимость амплитуды от частоты и от направления синусоиды.
Амплитуды отображаются в виде яркостей.
Нулевая частота – в центре спектра, низкие частоты вокруг центра, высокие – дальше от центра.
Спектр обычно продублирован отражением от нулевой частоты.
В реальных изображениях чаще всего гораздо большие амплитуды имеют низкие частоты (и постоянная составляющая). Поэтому постоянную составляющую иногда удаляют, или применяют логарифмический масштаб отображения амплитуд, чтобы пара самый мощных гармоник не скрыла остальные, менее мощные, но тоже существенные гармоники.

Спектральный анализ
Примеры изображений и их спектров
Видно, что спектр одной синусоиды – это точка
(не забываем про симметричное отражение спектра)
Две синусоиды – две точки

Спектральный анализ
Примеры изображений и их спектров
По спектру прослеживаются преобладающие направления в исходной картинке
Много высоких частот в спектре – много мелких деталей в исходном изображении

Спектральный анализ
Отображение спектра звука
График зависимости амплитуды от частоты
Низкие частоты – слева, высокие – справа
Часто применяется логарифмический масштаб частот и амплитуд: “log-log-спектр”
Временное и частотное разрешение спектра
Децибелы:
A1 – амплитуда измеряемого сигнала,
A0 – амплитуда сигнала, принятого за начало отсчета (0 дБ)
Разница на 6 дБ – разница по амплитуде в 2 раза,
разница на 12 дБ – разница по амплитуде в 4 раза.
Часто за 0 дБ принимается либо самый тихий слышимый звук, либо самый громкий звук, который может воспроизвести аудио-устройство.

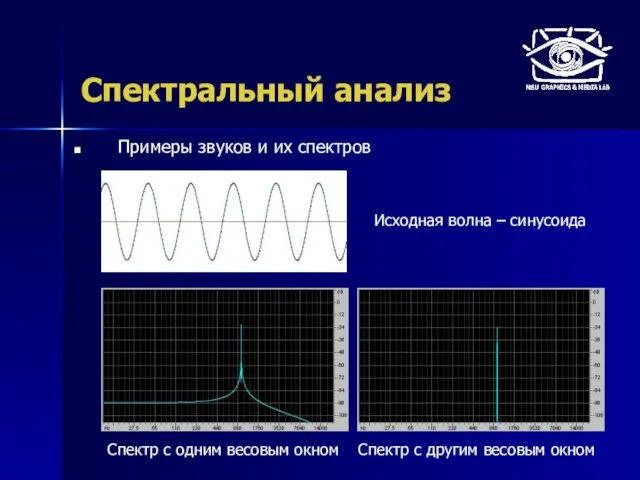
Спектральный анализ
Примеры звуков и их спектров
Исходная волна – синусоида
Спектр с одним весовым окном
Спектр с другим весовым окном

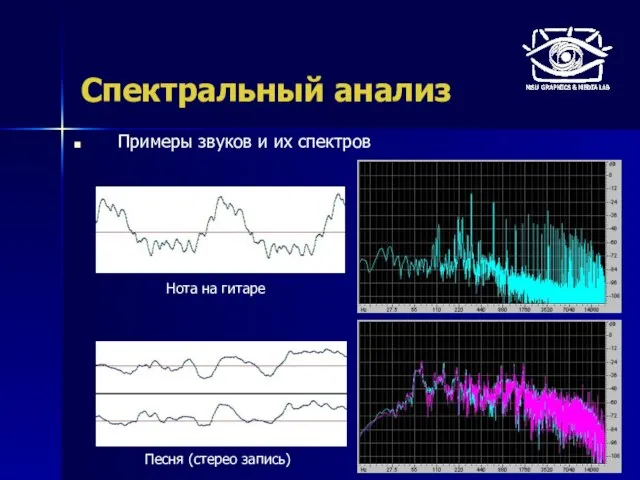
Спектральный анализ
Примеры звуков и их спектров
Песня (стерео запись)
Нота на гитаре

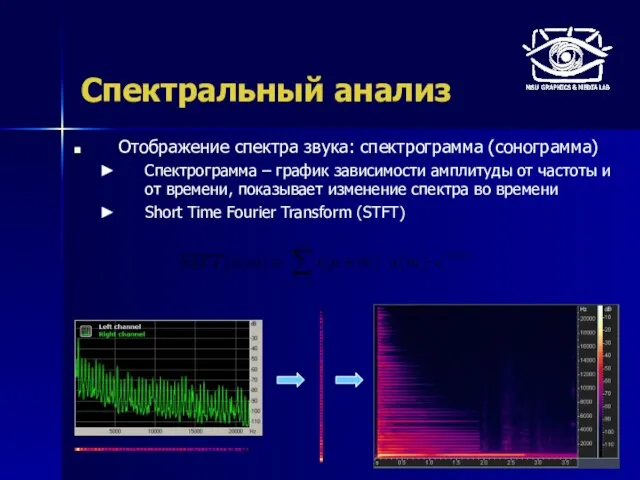
Спектральный анализ
Отображение спектра звука: спектрограмма (сонограмма)
Спектрограмма – график зависимости амплитуды от частоты и от времени, показывает изменение спектра во времени
Short Time Fourier Transform (STFT)

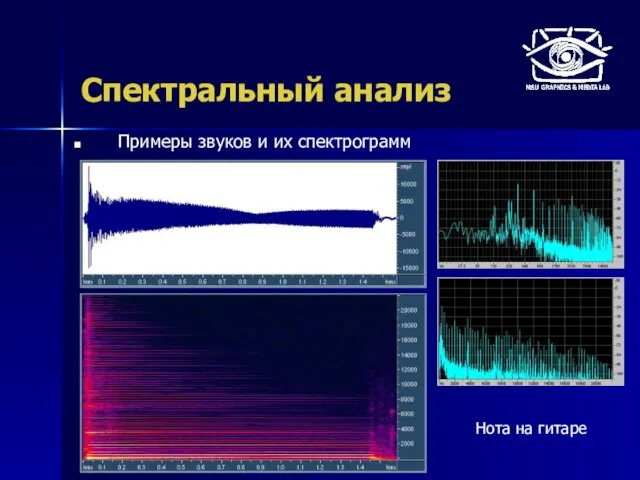
Спектральный анализ
Примеры звуков и их спектрограмм
Нота на гитаре

Свертка и фильтрация
Основные термины
Свертка (convolution), фильтрация (filtering)
Фильтр (filter), ядро фильтра (kernel)
Импульсная, частотная и фазовая характеристики (impulse, frequency, phase response)
Применения фильтрации
Анти-алиасинг изображений, нахождение границ
Звуковой эквалайзер
Моделирование реверберации помещения

Быстрая свертка
Прямое вычисление: M·N умножений (M – размер ядра свертки, N – длина сигнала)
Теорема свертки: свертка* во временной области эквивалентна умножению в частотной области, умножение во временной области эквивалентно свертке* в частотной области.
Алгоритм быстрой свертки:
Вычислить спектры сигнала и ядра свертки (FFT)
Перемножить эти спектры
Вернуть полученный спектр во временную область (IFFT)
Почему это быстрее? Потому что переход в частотную область и обратно быстрый: FFT
* Речь идет о т.н. круговой свертке

Быстрая свертка
Как изменяется длина сигнала при свертке? Она увеличивается на длину ядра минус 1 (т.к. каждый входной отсчет превращается в ядро и они складываются с наложением)
Значит, если взять сигнал длины N, ядро длины M и произвести свертку через FFT размера N, то результат свертки (длины N+M-1) не поместится в результате IFFT (длины N). Произойдет круговая свертка (заворачивание результата по времени).
Следовательно, для предотвращения круговой свертки надо взять размер FFT как минимум N+M-1

Фильтрация
Спектры сигналов при свертке перемножаются
Следовательно, свертка (фильтрация) меняет спектр сигнала
Свойства фильтров:
Частотная характеристика фильтра (АЧХ)
Полосы пропускания (pass-band), подавления (stop-band), среза (transition band)
Линейность ФЧХ
Длина фильтра
*
=
Перемножение амплитуд = сложение децибелов

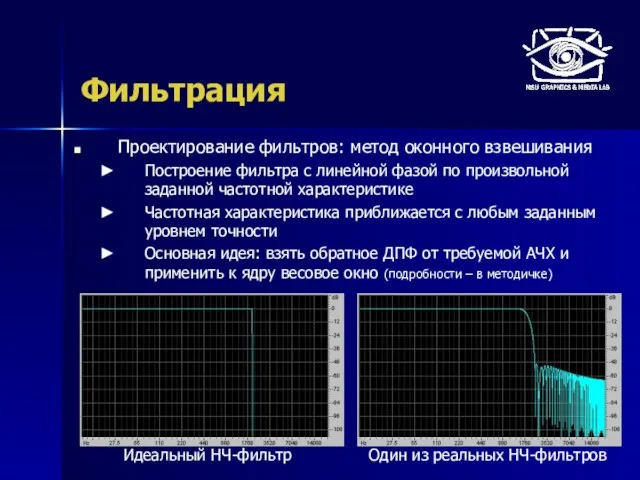
Фильтрация
Проектирование фильтров: метод оконного взвешивания
Построение фильтра с линейной фазой по произвольной заданной частотной характеристике
Частотная характеристика приближается с любым заданным уровнем точности
Основная идея: взять обратное ДПФ от требуемой АЧХ и применить к ядру весовое окно (подробности – в методичке)
Идеальный НЧ-фильтр
Один из реальных НЧ-фильтров

Фильтрация
Применения фильтрации
Подавление помех и шумов
Анти-алиасинг
Звуковые эквалайзеры: улучшение качества звука, компенсация искажений звуковой аппаратуры, творческие задачи в звукозаписи
Моделирование реверберации
Обработка изображений: эффекты, коррекция
Фильтрация – составная часть многих других, более сложных алгоритмов

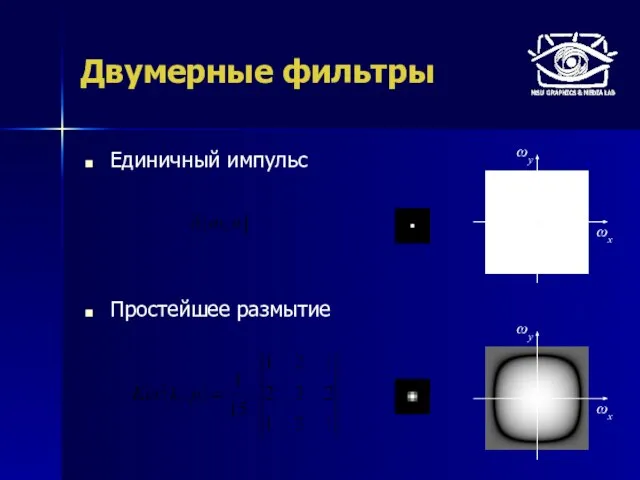
Единичный импульс
Простейшее размытие
Двумерные фильтры

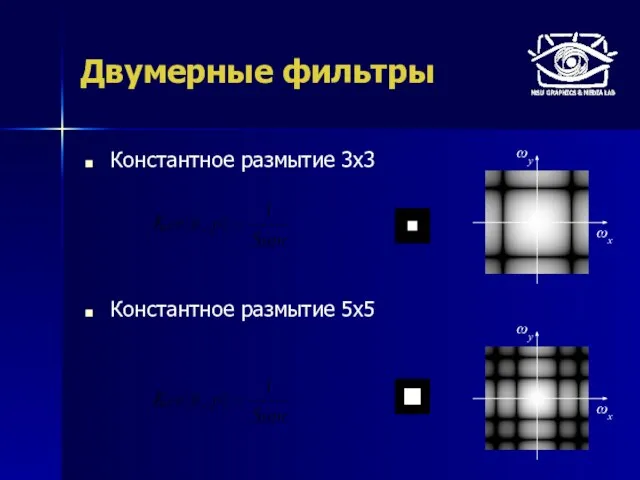
Константное размытие 3х3
Константное размытие 5х5
Двумерные фильтры

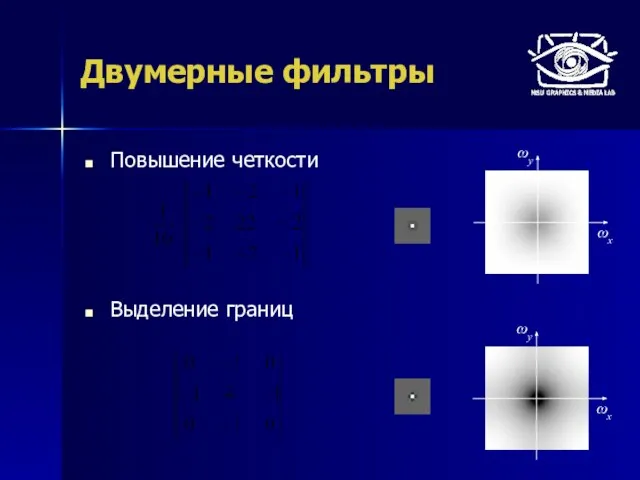
Повышение четкости
Выделение границ
Двумерные фильтры

Тиснение
Пример спектра изображения
Двумерные фильтры

Эквалайзеры
Эквалайзер – устройство коррекции тембра сигнала, изменяющее амплитуды его частотных составляющих
Изначально применялись для выравнивания АЧХ неидеального звукового тракта
Вскоре стали использоваться и творчески, для создания нужных тембров или аккуратного совмещения инструментов в фонограмме

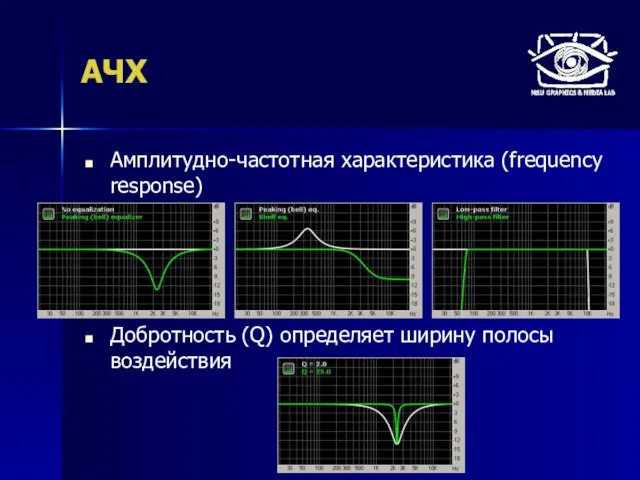
АЧХ
Амплитудно-частотная характеристика (frequency response)
Добротность (Q) определяет ширину полосы воздействия