Содержание
- 2. При изучении работы различных устройств компьютера приходится рассматривать такие его логические элементы, в которых реализуются сложные
- 3. Алгоритм построения таблиц истинности для сложных выражений: Определить количество переменных (простых выражений); Определить количество логических операций
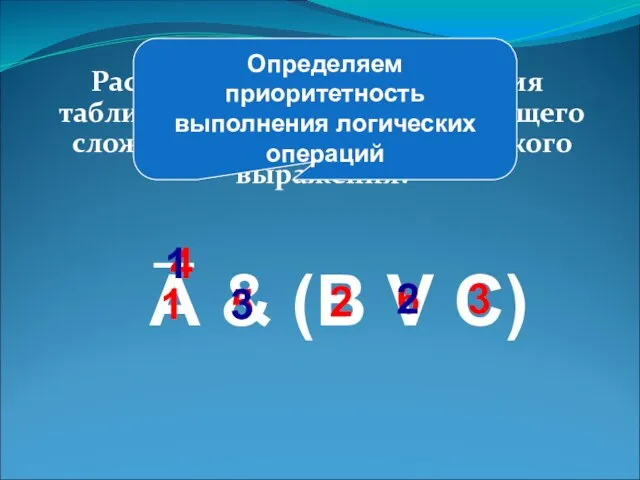
- 4. Порядок выполнения логических операций: Действия в скобках Инверсия Конъюнкция Дизъюнкция
- 5. Рассмотрим пример построения таблицы истинности для следующего сложного (составного) логического выражения: А & (B V C)
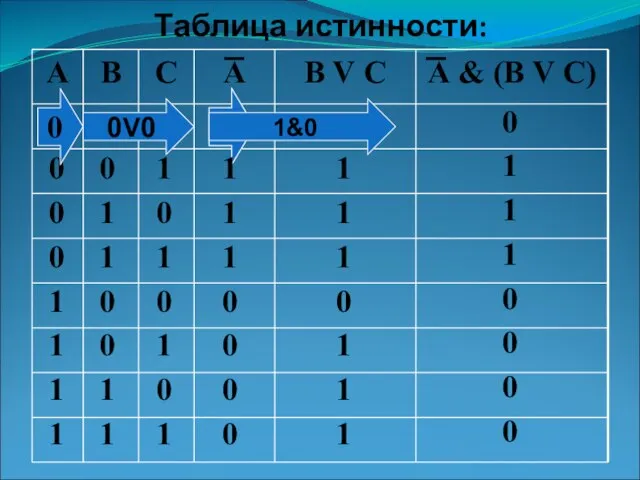
- 6. Решение: Простые выражения (логические переменные): А, В, С; (3) Количество логических операций: ¬ А - инверсия;
- 7. 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1
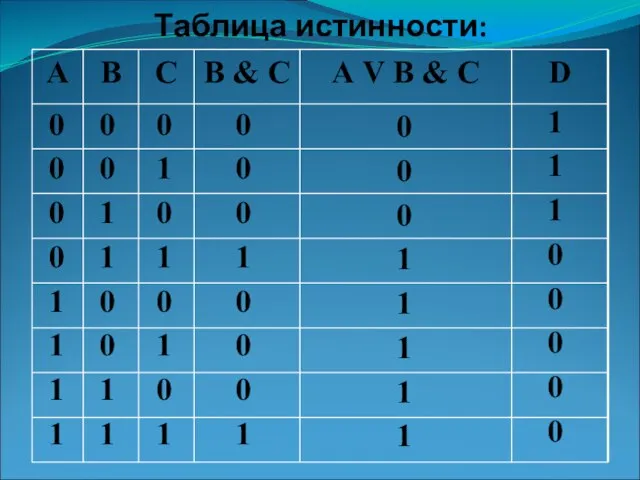
- 8. Постройте таблицу истинности для логического выражения: D=А V B & C
- 9. 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1
- 11. Скачать презентацию





 Лагерь с дневным пребыванием
Лагерь с дневным пребыванием Колыбельные
Колыбельные Детский технопарк Кванториум
Детский технопарк Кванториум Использование СМС технологий в высоконагруженных WEB проектах. Дмитрий Булычков. - презентация
Использование СМС технологий в высоконагруженных WEB проектах. Дмитрий Булычков. - презентация С новым годом, люди!!!
С новым годом, люди!!! Игры в расширенной форме.Информация
Игры в расширенной форме.Информация Кем можно хвалиться?
Кем можно хвалиться? Организационно – педагогические условия эффективности воспитательного процесса в вузе
Организационно – педагогические условия эффективности воспитательного процесса в вузе День Земли
День Земли Швеция в Петербурге
Швеция в Петербурге Презентация на тему Водные ресурсы мира
Презентация на тему Водные ресурсы мира  Н.И Вавилов
Н.И Вавилов Человек в системе экономических отношений
Человек в системе экономических отношений Модель современного менеджмента
Модель современного менеджмента « Сколько весит здоровье ученика?» Составили: ученики 3-б класса Руководитель: Просвирнина Н.П учитель начальных классов МОУ-СОШ№2
« Сколько весит здоровье ученика?» Составили: ученики 3-б класса Руководитель: Просвирнина Н.П учитель начальных классов МОУ-СОШ№2 Давайте дружить
Давайте дружить Город, в котором мы живем
Город, в котором мы живем Паспорт безопасности
Паспорт безопасности Органоиды клетки
Органоиды клетки Дмитрий Сергеевич Мережковский
Дмитрий Сергеевич Мережковский Фазовые переходы
Фазовые переходы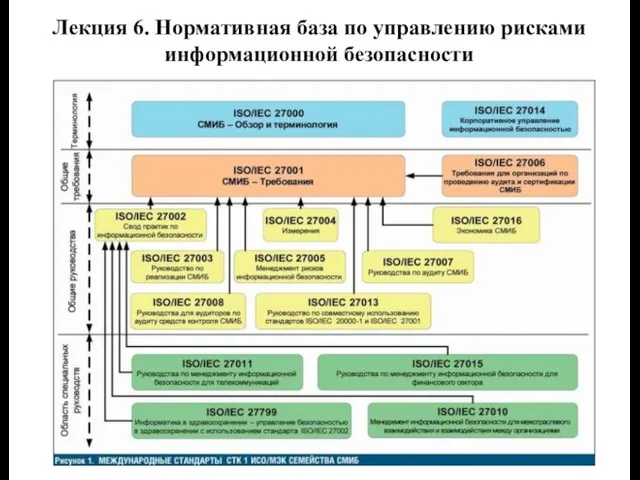 Нормативная база по управлению рисками информационной безопасности. Лекция 6
Нормативная база по управлению рисками информационной безопасности. Лекция 6 Йод
Йод Организация Объдиненных Нациий
Организация Объдиненных Нациий «ЭНЕРГЕТИКА ДОМА».
«ЭНЕРГЕТИКА ДОМА». 9 June 2009
9 June 2009 ТЕХНОЛОГИЯ
ТЕХНОЛОГИЯ Внеклассное мероприятие«Как хорошо, когда мы вместе».
Внеклассное мероприятие«Как хорошо, когда мы вместе».