Слайд 2Порядок расчёта токов КЗ:
1. Составляют расчётную схему СЭС.
2. Составляют её эквивалентную схему

замещения.
3. Определяют параметры всех элементов схемы замещения (ЭДС, сопротивления и др.)
4. Преобразовывают и упрощают схему замещения до простейшего вида.
5. Вычисляют токи КЗ.
Слайд 31. Составление схем замещения и расчет их параметров.

Слайд 4Расчёт токов КЗ начинается с составления расчётной схемы.
Так как рассматриваемая система

является симметричной трёхфазной системой, то расчёт можно вести на одну фазу и пользоваться при этом однолинейным изображением схем.
Слайд 51.1 Расчётная схема – это упрощенная однолинейная схема электрической системы, включающая все

источники и все элементы системы, по которым протекают токи КЗ (с перспективой на 5 лет, составляется по принципи-альной схеме системы).
Источники : все синхронные генера-торы, система, а также работающие СД и АД, мощностью более 100 кВт.
Слайд 61.2 Схема замещения электрической системы представляет собой совокупность схем замещения отдельных элементов,

соединённых в той же последовательности, что и на расчётной схеме.
ОСОБЕННОСТЬ !
Слайд 7При расчёте токов КЗ схема замещения составляется для сверхпереходного режима, т.е. источники

представляются в ней своими сверхпереходными ЭДС Ed´´ и сверхпереходными индуктивными сопротивлениями xd´´
Слайд 8Рисунок 1,а – Представление элементов электрической системы в схемах замещения
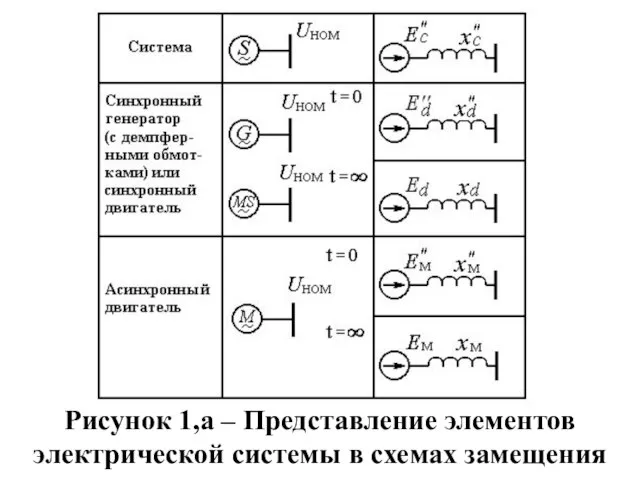
Слайд 9Рисунок 1,б – Представление элементов электрической системы в схемах замещения
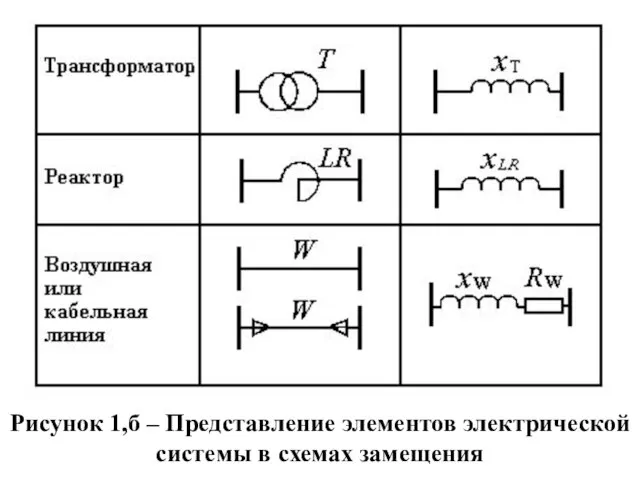
Слайд 10Рисунок 2 – Пример расчетной (а) и
эквивалентной (б) схемы
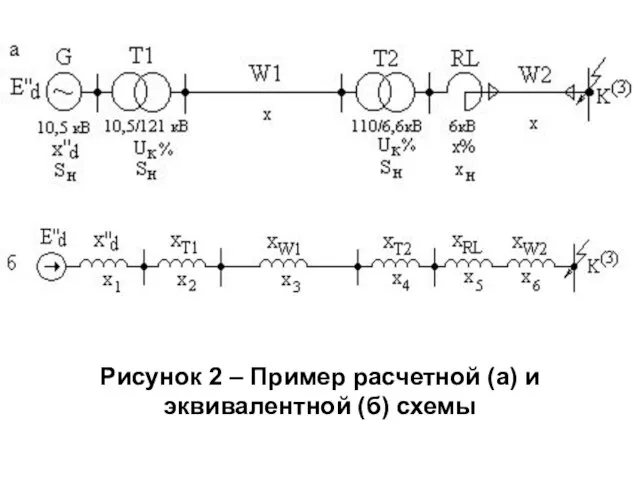
Слайд 11Порядок расчёта токов КЗ:
1. Составляют расчётную схему СЭС.
2. Составляют её эквивалентную схему

замещения.
3. Определяют параметры всех элементов схемы замещения (ЭДС, сопротивления и др.)
4. Преобразовывают и упрощают схему замещения до простейшего вида.
5. Вычисляют токи КЗ.
Слайд 121.3 Параметры элементов схемы замещения (сопротивления), как и параметры режима (напряжения, тока,

мощности) могут быть выражены как в системе имено-ванных единиц, так и в системе относительных единиц.
Точность результатов расчёта не зависит от выбранной системы единиц !
Слайд 13В системе именованных единиц параметры E, U, I, Z, X, r, S

выражаются в [ В, А, Ом, ВА] или в их производных.
Если в расчётной схеме имеются трансформаторы, т.е. разные ступени напряжения, то все параметры схемы замещения приводятся к основной (базисной) ступени напряжения.
Слайд 14Рекомендуется за базисную ступень напряжения применять ту ступень, где находится точка КЗ.
Именованные

величины, преобразованные к базисной ступени напряжения, называются приведёнными и обозначаются кружочком сверху.
Слайд 16(1) – формулы для точного приведения.
В практических расчётах часто используют приближённое приведение

как в именованных, так и относительных системах единиц. Оно заключается в том, что для каждой ступени трансформации устанавливают среднее номинальное напряжение Uср. по специальной шкале [1, с. 61]
Слайд 17Рисунок 2 – Пример расчетной (а) и
эквивалентной (б) схемы
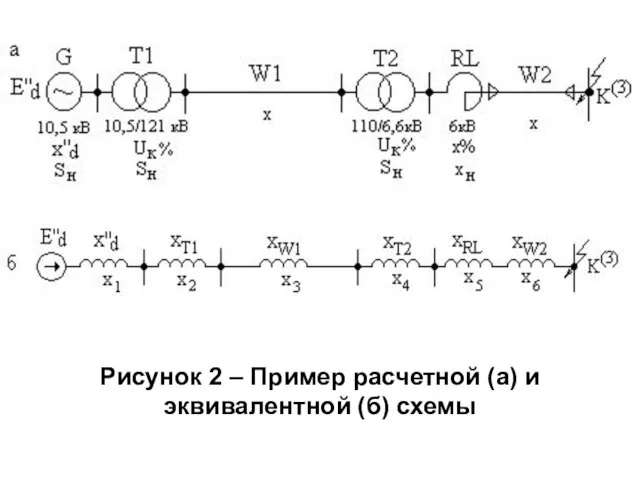
Слайд 18Тогда приведение упрощается и (1) для именованных величин принимают вид (2):
(2)

Слайд 19Расчёты в именованных единицах проводят, как правило:
- когда исходные данные (параметры элементов

схемы) указаны в именованных единицах;
- в сетях с напряжением менее 1 кВ.
Слайд 20На практике чаще используют относительные единицы. Расчёты в них часто существенно упрощаются,

облегчается контроль расчётных данных и сопоставление результатов расчёта для установок различной мощности, т.к. для таких установок относительные значения расчётных величин имеют одинаковый порядок.
Слайд 21В относительных номинальных величинах за единицу измерения принимают номинальные значения своих параметров:

Uн, Iн, Sн, Xн. Тогда относительные номинальные значения будут иметь вид:
(3)
Слайд 22Расчёты токов КЗ в установках выше 1 кВ чаще производят в относительных

базисных единицах. В них истинные значения параметров делятся на базисные значения.
(4)
Слайд 23Базисных величин всего четыре.
На практике две из базисных величин выбираются произвольно:
базисную мощность

Sб – кратную десяти, например: 10 МВА, 100 МВА и др.;
базисное напряжение Uб рекомендуется выбирать по напряжению в точке КЗ;
остальные две выбирают из выражений
Слайд 24Если в расчётной схеме имеются трансформаторы, то для относительных базисных единиц, как

и для именованных, проводится точное или приближенное приведение к основной (базисной) ступени напряжения.
При приближенном приведении в выражениях (4) заменяют
Слайд 25Если исходные данные приведены в относительных номинальных единицах, то для преобразования их

в относительные базисные единицы используют формулы:
Ср. знач. парам. элементов см. [4] с.14, 15, 22.
Слайд 26 Выводы:
1. Эквивалентная схема замещения по своей сути представляет математическую модель, в

которой реальные элементы электрической системы замещаются их сопротивлениями (индуктивными или полными).
2. Для расчетов токов КЗ эквивалентные схемы составляются для сверхпереходного режима.
3. Параметры схем замещения в электрических сетях выше 1000 В, как правило, выражаются в относительных базисных единицах, а в сетях ниже 1000 В – в именованных единицах.
4. При, наличии трансформаторов параметры схем замещения приводят к базисной ступени напряжения (где находится точка КЗ).
Слайд 272. Преобразование схем замещения.

Слайд 28Порядок расчёта токов КЗ:
1. Составляют расчётную схему СЭС.
2. Составляют её эквивалентную схему

замещения.
3. Определяют параметры всех элементов схемы замещения (ЭДС, сопротивления и др.)
4. Преобразовывают и упрощают схему замещения до простейшего вида.
5. Вычисляют токи КЗ.
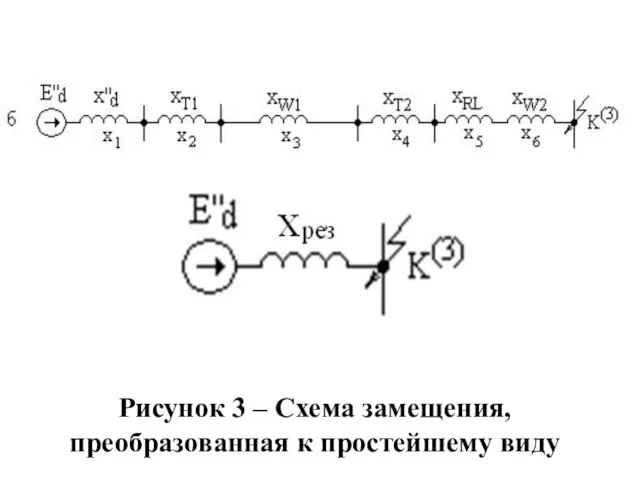
Слайд 29Простейшая схема – это эквивалентная схема, состоя-щая из одного результирующего сопротивления хрез

, с одной стороны к которому приложена
расчетная ЭДС , а с другой – находится расчетная точка КЗ с нулевым потенциалом (нарисуйте её).
Слайд 30Рисунок 3 – Схема замещения, преобразованная к простейшему виду
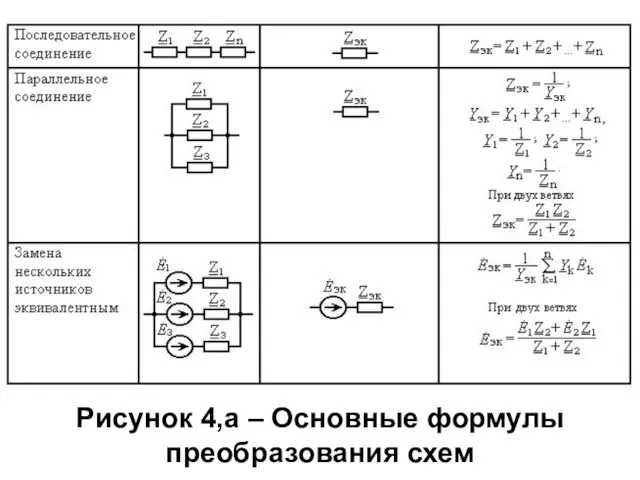
Слайд 31Рисунок 4,а – Основные формулы преобразования схем
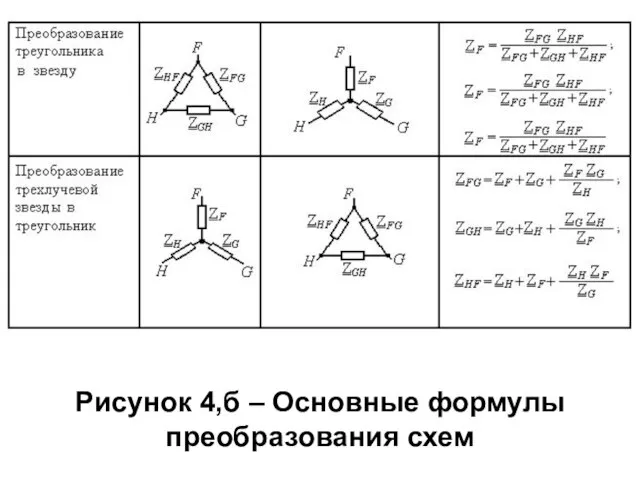
Слайд 32Рисунок 4,б – Основные формулы преобразования схем
Слайд 33Выводы:
1. Целью преобразования схемы замещения является приведение ее к простейшему виду.
2. Преобразование

включает в себя последовательное и параллельное сложение сопротивлений, последовательное преобразование треугольника сопротивлений в звезду и обратно.
Слайд 34Задание на самостоятельную подготовку:
1. Изучить материал лекции по конспекту.
2. То же по

рекомендованной литературе:
[2], с. 85-96 – основная;
[1], с. 53-70; [4], с. 5-23 – дополнительная.

































 Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит
Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит NXP semiconductors, Москва. Краткий обзор
NXP semiconductors, Москва. Краткий обзор Однофазный TIG-инвертор
Однофазный TIG-инвертор Індекси цін у будівництві
Індекси цін у будівництві Банки и банковская система РФ. Тест
Банки и банковская система РФ. Тест Прикладной Тайм-менеджмент для программистов
Прикладной Тайм-менеджмент для программистов ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет
ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет Кабинет министров
Кабинет министров Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: +
Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: + Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки
Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки Сессия Госконтроль 2.0: образ будущего
Сессия Госконтроль 2.0: образ будущего Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Перпендикуляр и наклонные
Перпендикуляр и наклонные Однородные члены предложения
Однородные члены предложения Предмет, метод, источники и принципы Трудового права
Предмет, метод, источники и принципы Трудового права Поэты Ставрополья о родном крае и о природе родного края
Поэты Ставрополья о родном крае и о природе родного края Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр
Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр Обзор на персонажа
Обзор на персонажа ВКР: Действительный цикл машины МВВ6 - 1 -2
ВКР: Действительный цикл машины МВВ6 - 1 -2 15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом).
15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом). Правила наложения жгутов повязок и шин
Правила наложения жгутов повязок и шин Вальдорфская система образования
Вальдорфская система образования Social Ecology Sustainable Development
Social Ecology Sustainable Development  Ваш профессиональный маршрут
Ваш профессиональный маршрут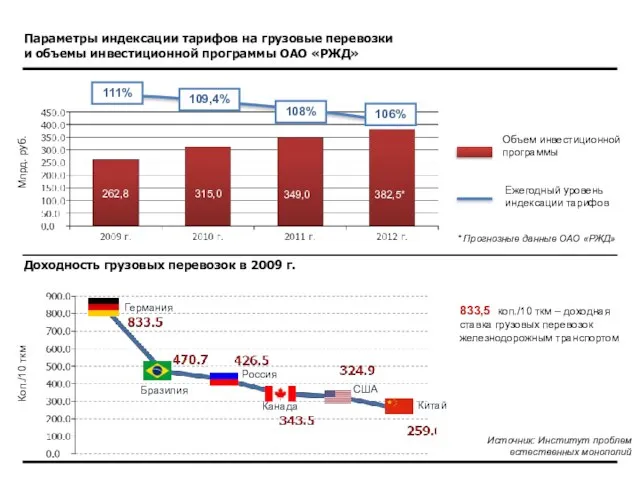 Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД»
Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД» Концепция воспитательной системы
Концепция воспитательной системы Технология создания и редактирования изображений в векторном редакторе
Технология создания и редактирования изображений в векторном редакторе Презентация на тему Использования краеведческого материала в образовательном процессе
Презентация на тему Использования краеведческого материала в образовательном процессе