Основы теории принятия решений. Лекция 3

Содержание
Алгоритм Delta-1
Алгоритм Gamma-1
Выбор алгоритмов таксономии.
Пример 1.
Примеры прикладных задач таксономии:
прогнозирование успеваемости;
ранжирование объектов.

Таксономия в λ-пространстве с заданным числом таксонов
Цель: распределить по W таксонам N объектов с неоднородными характеристиками.
Реализация: алгоритм Delta-1.
Отличие от алгоритма Forel-2: неоднородность характеристик объектов.

Алгоритм DELTA1
Шаг 1. Ищется λ - расстояние между каждой парой объектов.
Шаг 2. Строится полный взвешенный неориентированный граф G(X,U), вершины
которого отвечают объектам, а каждого рёбра (p,q) равен расстоянию между Xp и Xq.
Шаг 3. Алгоритмом Прима ищется минимальное связывающее подмножество рёбер, остальные рёбра удаляются.
Шаг 4. Полученный граф обозначить G(X,U0).
Шаг 5. i=1
Шаг 6. Выбор ребра (p,q) с максимальным весом.
Шаг 7. Ребро (p,q) отбрасывается: U0 = U0\(p,q).
Шаг 8. Если i =W, то перейти к шагу 10, нет - к шагу 9.
Шаг 9. i=i+1, перейти к шагу 6.
Шаг 10. Конец алгоритма.

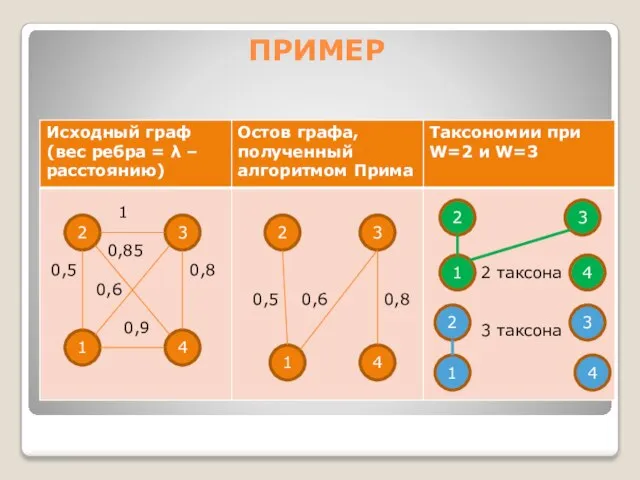
ПРИМЕР
2
4
3
1
2
4
3
1
1
0,85
0,5 0,8
0,6
0,9
0,5 0,6 0,8
2
1
4
3
2
3
4
1
2 таксона
3 таксона

САМОСТОЯТЕЛЬНО
Пользуясь DELTA 1, распределить по двум таксонам 5 объектов, каждый из которых обладает двумя разнородными характеристиками, заданными таблицей:

САМОСТОЯТЕЛЬНО
Пользуясь алгоритмом DELTA 1, распределить по n таксонам 5 объектов, каждый из которых обладает двумя разнородными характеристиками, заданными на следующих двух слайдах

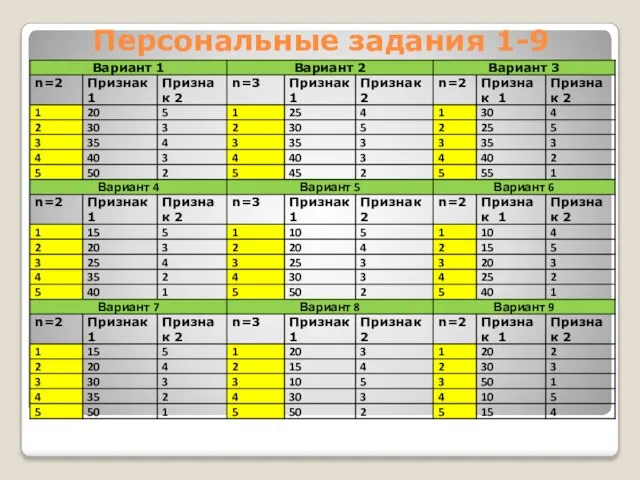
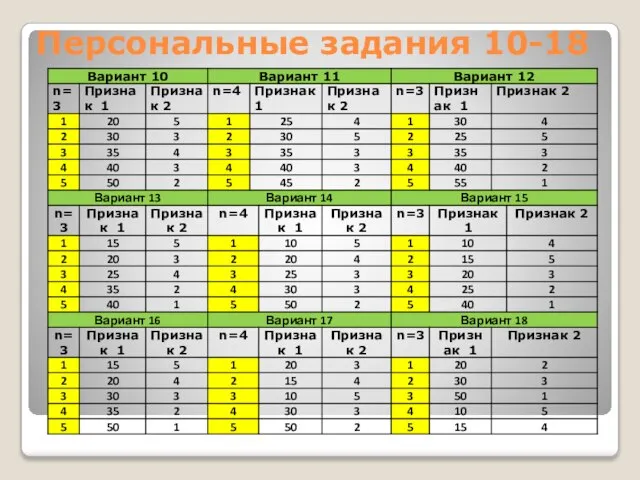
Персональные задания 1-9

Персональные задания 10-18

САМОСТОЯТЕЛЬНО
Изменить алгоритм Delta-1 таким образом, чтобы минимизировать верхнюю границу числа объектов, принадлежащих одному таксону (т.е. сделать распределение объектов между таксонами равномерным).
Пользуясь приведенными выше персональными заданиями решить эту задачу при условии, что число таксонов n=2.

Парное сравнение алгоритмов таксономии алгоритмом Gamma-1.

Обозначения и определения
Назначение алгоритма Gamma-1 заключается в том, чтобы попарно сравнивать различные алгоритмы таксономии. Для формального описания этого подхода далее используются следующие обозначения:
Si - таксономия, полученная i -м алгоритмом; «p» и «q»,- объекты;
ri(p,q) - расстояние между «p» и «q», полученное i-м алгоритмом:
(Очевидно, что ∀ p, ri(p,p)=0).
Величины ri(p,q) образуют матрицу μi ( mxm матрица). ri(p,q) =0, если p и q принадлежат одному таксону и ri(p,q) =1, p и q принадлежат разным таксонам.

Алгоритм Gamma-1
Шаг 1. Генерация матрицы μ1.
Шаг 2.. Генерация матрицы μ2.
Шаг 3. Определение максимального числа несовпадающих элементов β = m(m-1).
Шаг 4. Генерация новой матрицы μ3, каждый элемент которой r3(p,q) равен
r3(p,q) = |r1(p,q)-r2(p,q) |/ β.
Шаг 5. Вычисление критерия F, равного сумме всех r3(p,q) и представляющего собой нормированное расстояние Хемминга между μ1 и μ2.
Шаг 6. Конец алгоритма.

Пример: парное сравнение алгоритмов таксономии
Пользуясь алгоритмом Gamma-1, матрицы μ1 и μ2 которого соответственно равны:
определить величину F.

ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ “F”
F = 6/12 = 0.5
Матрица μ3 каждый элемент которой следует
умножить на 1/[4(4-1)] = 1/12.

Выбор алгоритма таксономии
Пусть Si - таксономия m объектов, полученная i-м алгоритмом, Fi,j - нормированное расстояние Хемминга между i-м и j-м алгоритмами таксономии, полученное алгоритмом Gamma 1. Тогда характеристикой каждого i-го алгоритма Fi является сумма:
Лучшим является q-й алгоритм, для которого справедливо:

Пример 1: условия
Определить, пользуясь Gamma 1, наилучший и наихудший из трех алгоритмов таксономии, матрицы μ1, μ2 и μ3 которых соответственно равны:
μ1= μ2= μ3=

Пример 1: решение
Вычисление характеристик каждого i-го алгоритма Fi (i=1,2,3):
Μ12= F12 =0,41; M13 = F13=0,667;
M23= F23=0,667. F1= F12 +F13 =1,077;
F2= F12 +F23=1,077;
F3= F13 +F23=1,334;
Лучшие алгоритмы- первый и второй, худший – третий.

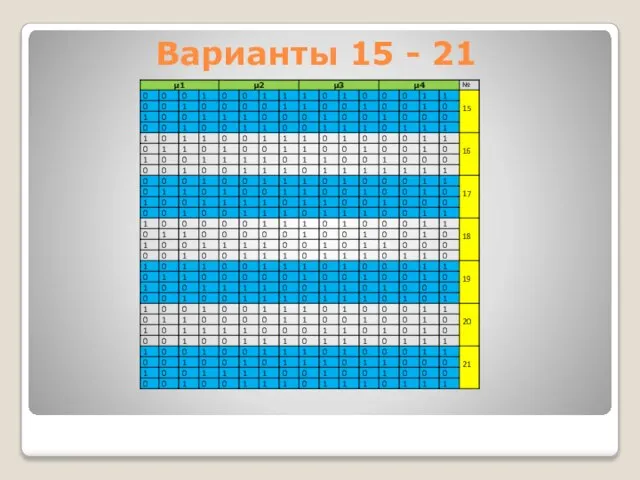
САМОСТОЯТЕЛЬНО
Определить наилучшую из четырех таксономий, представленных матрицами μ1, μ2 , μ3 и μ4 на следующих трех слайдах. Номера вариантов указаны в правом столбце матрицы персональных данных.

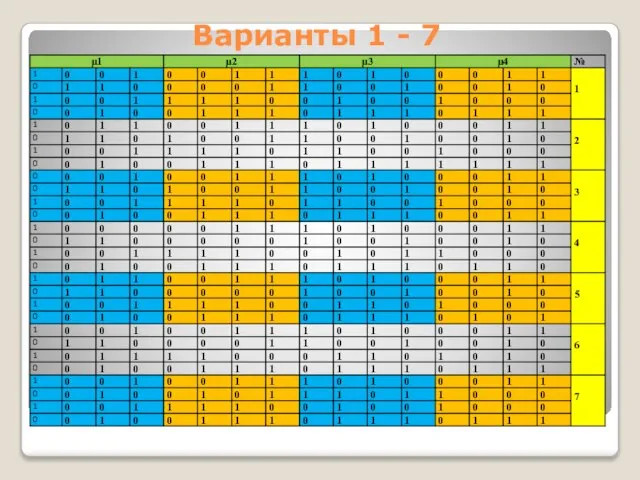
Варианты 1 - 7

Варианты 8 - 14

Варианты 15 - 21

Примеры прикладных задач таксономии
Прогнозирование успеваемости.
Ранжирование студентов.

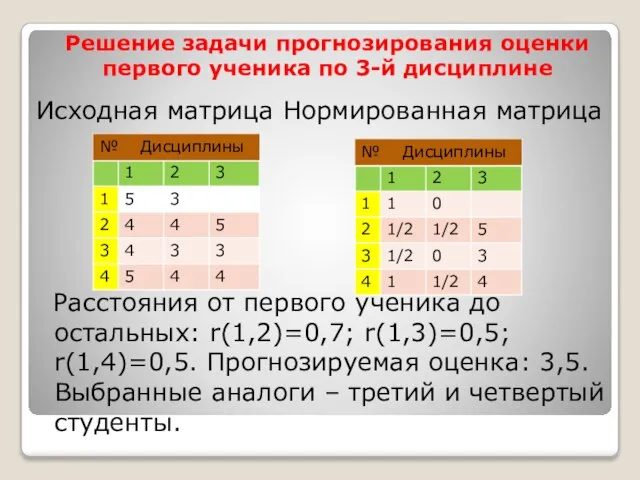
Прогнозирование успеваемости – содержательная постановка задачи.
Задана матрица, содержащая данные об оценках 3-х студентов по трем дисциплинам и одного – по первым двум. Требуется для последнего студента найти аналога среди первых двух, чтобы спрогнозировать его успеваемость по третьей дисциплине.

Решение задачи прогнозирования оценки первого ученика по 3-й дисциплине
Исходная матрица Нормированная матрица
Расстояния от первого ученика до остальных: r(1,2)=0,7; r(1,3)=0,5; r(1,4)=0,5. Прогнозируемая оценка: 3,5. Выбранные аналоги – третий и четвертый студенты.
№ Дисциплины
№ Дисциплины

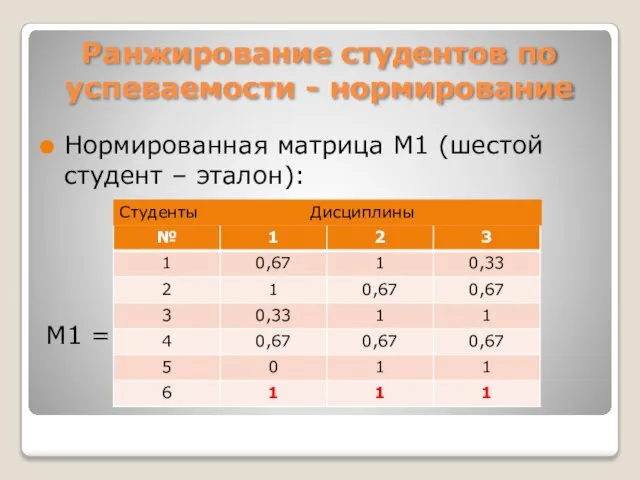
Ранжирование студентов по успеваемости - условия
Задана матрица М, содержащая данные об оценках 5-х студентов по трем дисциплинам. Требуется ранжировать их относительно отличника.
М =
Предложите a priori Вашу версию ранжирования.
№ Дисц.1 Дисц.2 Дисц.3

Ранжирование студентов по успеваемости - нормирование
Нормированная матрица М1 (шестой студент – эталон):
М1 =
Студенты Дисциплины

Ранжирование студентов по успеваемости - упорядочение
Расстояния от i-го студента до шестого (0
r(1,6)=0,74868;
r(2,6)=0,46669;
r(3,6)=0,67;
r(4,6)=0,5715;
r(5,6)=1.
Ранжирование студентов:
π = {2, 4, 3, 1, 5}

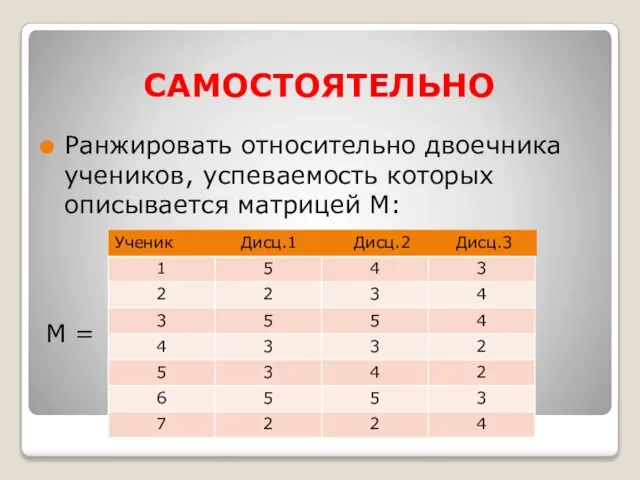
САМОСТОЯТЕЛЬНО
Ранжировать относительно двоечника учеников, успеваемость которых описывается матрицей М:
М =
Ученик Дисц.1 Дисц.2 Дисц.3

САМОСТОЯТЕЛЬНО
Определить прогноз оценки первого ученика по третьей дисциплине, полагая, что:
Эта оценка неизвестна;
Исходные данные приведены в матрице М на предыдущем слайде.