Содержание
- 2. План лекции: 1. Статистические гипотезы в медико- биологических исследованиях. 2. Параметрические критерии различий. 3. Непараметрические критерии.
- 3. Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотез. Задачи статистической проверки гипотез: Относительно
- 4. Статистическая гипотеза- это предположение о виде распределения или о величинах неизвестных параметров генеральной совокупности, которая может
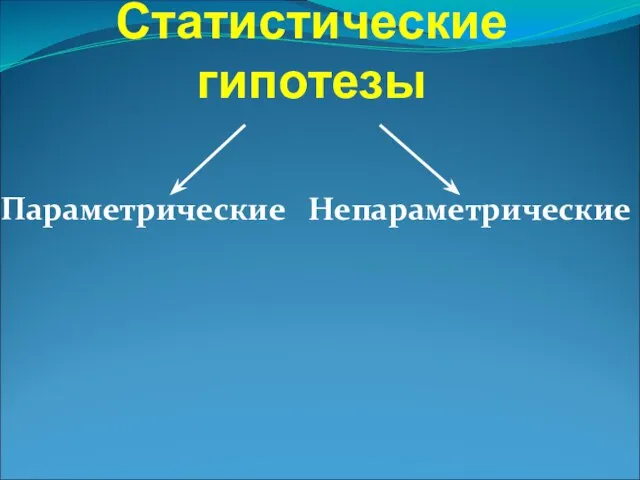
- 5. Статистические гипотезы Параметрические Непараметрические
- 6. Нулевой гипотезой Н0 называется основная гипотеза, которая проверяется. Альтернативной гипотезой Н1, называется гипотеза, конкурирующая с нулевой,
- 7. Основной принцип проверки гипотез Проверку гипотез осуществляют на основании результатов выборки X1,X2,…,Xn , из которых формируют
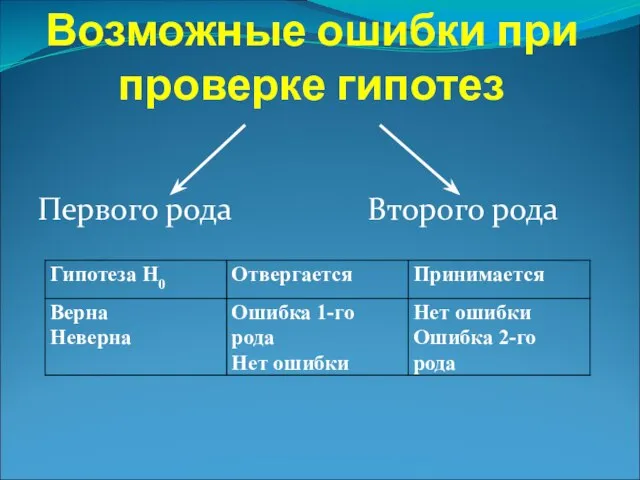
- 8. Возможные ошибки при проверке гипотез Первого рода Второго рода
- 9. Уровнем значимости критерия (α) называется вероятность допустить ошибку 1-го рода. Вероятность ошибки 2-го рода обозначается через
- 10. Методика проверки гипотез: 1. Формирование нулевой Н0 и альтернативной Н1 гипотез исходя из выборки X1,X2,…,Xn .
- 11. t-критерий Стьюдента: Общий вид:
- 12. Случай независимых выборок. df= n1+n2-2 n1=n2=n df=n-1 n1≠n2
- 13. Случай зависимых выборок. df=n-1
- 14. Вывод: Критерий Стьюдента может быть использован для проверки гипотезы о различии средних только для двух групп.
- 15. F- критерий Фишера: σ1>σ2 df1=n1-1, df2=n2-1
- 16. Критерии различия называют непараметрическими, если он не базируется на предположении о типе распределения генеральной совокупности и
- 17. Непараметрические критерии представлены основными группами: критерии различия между группами независимых выборок; критерии различия между группами зависимых
- 18. Различия между независимыми группами U критерий Манна-Уитни двухвыборочный критерий Колмогорова – Смирнова.
- 19. Различия между зависимыми группами z – критерий знаков Т – критерий Уилкоксона парных сравнений
- 20. Критерии согласия: Критерием согласия называют статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Пирсона (Хи-квадрат),
- 21. Критерий согласия χ2 (хи-квадрат) Пирсона. Н0: «между эмперическим распределением и теоретической моделью нет никакого различия». Если
- 22. Критерий согласия χ2 (хи-квадрат) Пирсона. n-объем выборки k-число интервалов разбиения выборки ni-число значений выборки, попавших в
- 23. Критерий согласия χ2 (хи-квадрат) Пирсона. или О-фактически наблюдаемое число Е- теоретически ожидаемое число
- 24. Поправка Йейтса Для распределения признаков, которые принимают всего 2 значения.
- 25. Правило применения критерия χ2. *По формуле вычисляют - выборочное значение статистики критерия. *выбрав уровень значимости α
- 26. ЛИТЕРАТУРА: Медик В.А.,Токмачев М.С.,Фишман Б.Б.Статистика в медицине и биологии. М.: Медицина, 2000. Лукьянова Е.А. Медицинская статистика.-
- 28. Скачать презентацию























 Центр гидравлики трубопроводного транспорта Академии наук Республики Башкортостан
Центр гидравлики трубопроводного транспорта Академии наук Республики Башкортостан Конкурс презентаций
Конкурс презентаций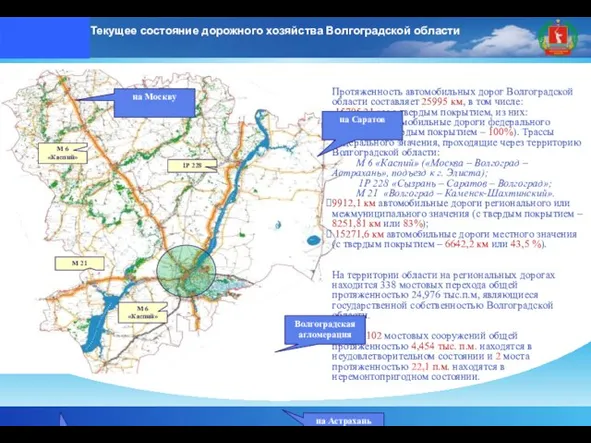 Текущее состояние дорожного хозяйства Волгоградской области
Текущее состояние дорожного хозяйства Волгоградской области Особенности экономического районирования России Подготовила: Клеутина С.А. Группа МЭ-092
Особенности экономического районирования России Подготовила: Клеутина С.А. Группа МЭ-092 TPG
TPG Глава 2
Глава 2 Джонатан Свифт. Слово о писателе. «Путешествие Гулливера» как сатира на государственное устройство общества. Образ Гулливера (час
Джонатан Свифт. Слово о писателе. «Путешествие Гулливера» как сатира на государственное устройство общества. Образ Гулливера (час Теория целей Локка
Теория целей Локка Как подобрать телефон для учебы работы игр
Как подобрать телефон для учебы работы игр Учителя русского языка
Учителя русского языка Правонарушения и юридическая ответственность
Правонарушения и юридическая ответственность В объятьях двух морей новый
В объятьях двух морей новый МОДЕЛЬ И АЛГОРИТМ ДЕЯТЕЛЬНОСТИ МОУ СОШ № 13 В УСЛОВИЯХ ВВЕДЕНИЯ Федерального государственного образовательного стандарта начал
МОДЕЛЬ И АЛГОРИТМ ДЕЯТЕЛЬНОСТИ МОУ СОШ № 13 В УСЛОВИЯХ ВВЕДЕНИЯ Федерального государственного образовательного стандарта начал Профилактикa и защита детей от насилия в школе
Профилактикa и защита детей от насилия в школе Шлифовальные станки, используемые в производстве фанеры
Шлифовальные станки, используемые в производстве фанеры Бухобслуживание
Бухобслуживание Портфель здоровья
Портфель здоровья Правило "ЕСЛИ-ТО"
Правило "ЕСЛИ-ТО" Русские народные праздники
Русские народные праздники О работе информационной системы «Единое окно доступа к образовательным ресурсам»
О работе информационной системы «Единое окно доступа к образовательным ресурсам» Русский язык и культура речи. Виртуальная выставка
Русский язык и культура речи. Виртуальная выставка Деловые документы (автобиография, заявление, резюме )
Деловые документы (автобиография, заявление, резюме ) 1 классМБОУ Великовская СОШ2011/2012 учебный год
1 классМБОУ Великовская СОШ2011/2012 учебный год Эквадор
Эквадор Презентация на тему Былины
Презентация на тему Былины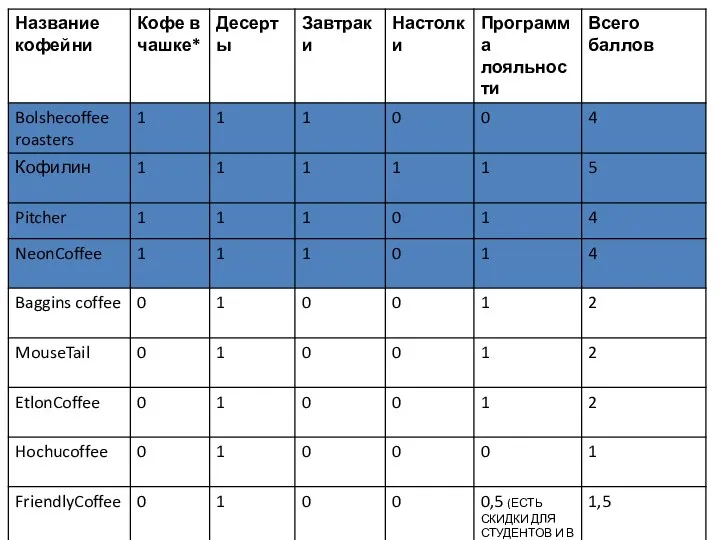 4. карта позиционирования, конкуренты_Шашина_3ГИВ13
4. карта позиционирования, конкуренты_Шашина_3ГИВ13 Нитяная графика
Нитяная графика Афанасий Фет и Фёдор Тютчев – певцы русской природы
Афанасий Фет и Фёдор Тютчев – певцы русской природы