ОТС-2 (2018)

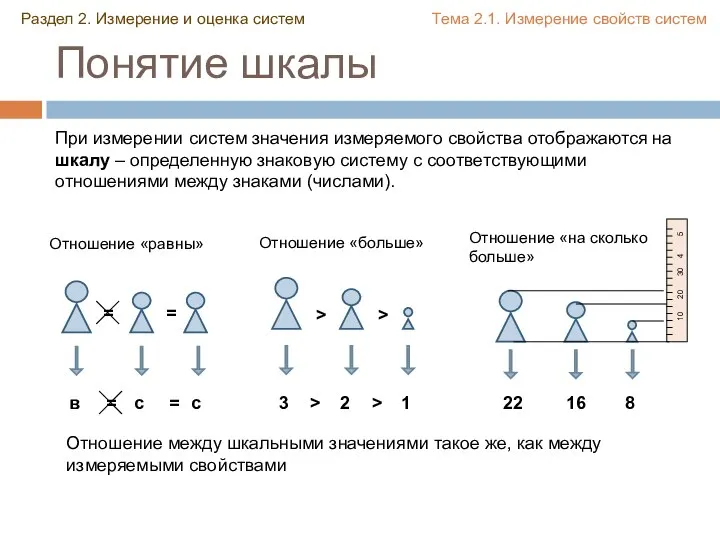
Понятие шкалы
При измерении систем значения измеряемого свойства отображаются на шкалу – определенную знаковую систему с соответствующими отношениями между знаками (числами).
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем
Отношение между шкальными значениями такое же, как между измеряемыми свойствами

Формальное определение
- эмпирическая система, включающая множество xi на которых задано некоторое отношение Rx
– знаковая система, включающая значения измеряемых свойств φ (xi) с отношением Ry
– гомоморфное отображение X на Y, такое, что:
только тогда, когда
Шкала:
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем

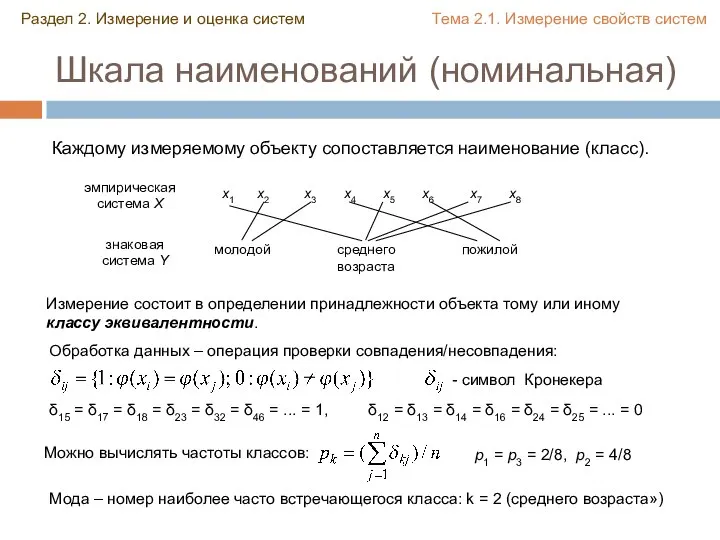
Шкала наименований (номинальная)
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем
Каждому измеряемому объекту сопоставляется наименование (класс).
Измерение состоит в определении принадлежности объекта тому или иному классу эквивалентности.
Обработка данных – операция проверки совпадения/несовпадения:
Можно вычислять частоты классов:
Мода – номер наиболее часто встречающегося класса: k = 2 (среднего возраста»)
δ15 = δ17 = δ18 = δ23 = δ32 = δ46 = ... = 1, δ12 = δ13 = δ14 = δ16 = δ24 = δ25 = ... = 0
p1 = p3 = 2/8, p2 = 4/8
- символ Кронекера

Шкала порядка (ранговая)
Позволяет упорядочить объекты, расположить их в соответствии с возрастанием или убыванием какого-либо качества.
Кроме отношений эквивалентности сохраняются отношения предпочтения:
если
то
Судя по рангам ничего нельзя сказать о расстояниях между объектами.
Над рангами нельзя производить арифметические операции. Допустимые операции:
нахождение частот и мод, как и для номинальной шкалы;
определение медианы - объекта с рангом, ближайшим к числу n/2 (x1);
разбиение всей выборки на части и др.
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем
- номер объекта в упорядоченном ряду (ранг)

Шкала интервалов
Позволяет измерять расстояния в некоторых единицах, одинаковых по всей длине шкалы. Начало координат произвольно.
Используется для величин, не имеющих абсолютного нуля (температура, время, высота местности).
При измерении в разных интервальных шкалах (температура по Цельсию и Фаренгейту) отношения двух интервалов должны быть одинаковыми для всех шкал:
Только интервалы имеют смысл настоящих чисел, и только над интервалами следует выполнять арифметические операции.
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем
Можно определить, на сколько (но не во сколько раз) свойство одного объекта превосходит то же свойство другого объекта

Шкала интервалов
Воду нагрели от 9°С до 18°С, а молоко от 9° С до 36°С
Неправильно: t воды увеличилась в 2 раза, t молока – в 4 раза.
Правильно: изменение t воды в 3 раза меньше, чем изменение t молока.
Соотношение сохраняется при переходе от шкалы Цельсия к шкале Фаренгейта: t°F = 1,8 t°C + 32
t воды была: 9°С = 48,2°F , t воды стала: 18°С = 64,4°F,
t молока была: 9°С = 48,2°F , t молока стала: 36°С = 96,8°F.
Отношение изменений температур воды и молока по Цельсию:
(18 - 9) / (36 - 9) = 9 / 27 = 1/3.
Отношение изменений температур воды и молока по Фаренгейту:
(64,4 – 48,2) / (96,8 – 48,2) = 16,2 /48,6 = 1/3.
Соотношение интервалов сохранилось.
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем
Пример

Шкала отношений
Позволяет оценить, во сколько раз свойство одного объекта превосходит то же свойство другого объекта.
Измеряемые величины имеют естественный абсолютный нуль (вес, длина).
Основное свойство - сохранение отношения двух шкальных значений при переходе от одной шкалы к другой
Значения, измеренные в шкале отношений, являются «полноправными» числами,
с ними можно выполнять любые арифметические действия.
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем
Абсолютная шкала
Имеет абсолютный нуль и абсолютную единицу. Пример - числовая ось.

Выбор шкалы
Выбор шкалы зависит от определяющего отношения.
Шкала наименований используется, если выполняются аксиомы тождества:
1. А = А (рефлексивность).
2. Если А= В, то В = А (симметричность).
3. Если А= В и В = С, то А = С (транзитивность).
Ранговая шкала используется, если выполняются аксиомы упорядоченности:
4. Если А ≠ В то либо А > В либо В > А. (антисимметричность).
5. Если А >В и В > С, то А > С (транзитивность).
Шкала интервалов используется, если дополнительно известны расстояния между объектами
Шкала отношений используется, если в выполняются аксиомы аддитивности:
6. Если А = Р и В > 0, то А + В > Р
7. А + В = В + А.
8. Если А = Р и В =Q, то А + В = Р+Q
9. (А + В)+ С= А + (В + С)
Для использования абсолютной шкалы необходимо наличие абсолютного нуля и абсолютной единицы
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем

Виды измерений
Объективные измерения – результат измерения объективен
Примеры: измерение времени, массы, температуры
Как правило, измерения производятся измерительными приборами
Субъективные измерения – результат мыслительной деятельности человека
Примеры: оценка качества продукции, комфортности условий труда, оценка важности показателей, степени соответствия требованиям
Как правило, измерения производятся экспертами или лицом, принимающим решения
Результатом является оценка – лингвистическое значение («плохо», «хорошо» ...) либо число, отражающее меру (интенсивность) выраженности качественного свойства или приоритет объекта среди множества других по данному свойству.
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем

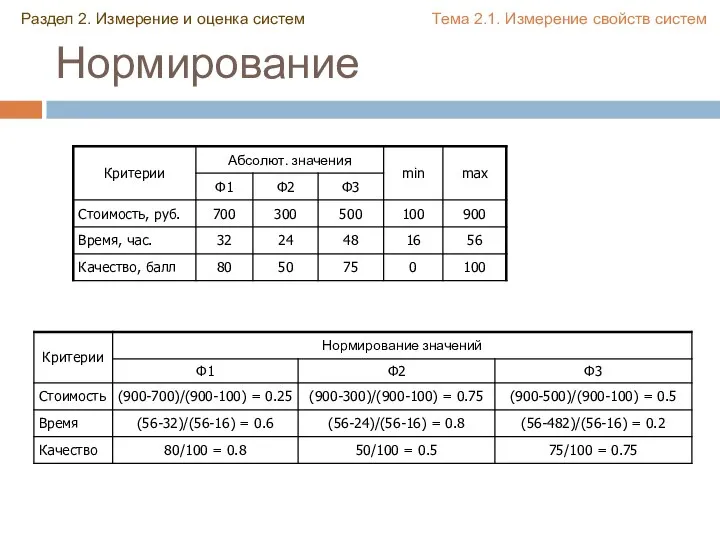
Интеграция измерений
Объекты могут быть измерены по множеству различных признаков (критериев).
Для удобства сравнения объектов необходима обобщенная (интегральная) оценка.
В случае если частные критерии имеют различную размерность,
то необходимо нормировать значения.
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем

Способы нормирования
В случае если чем абсолютное значение больше, тем оценка выше:
qij – оценка i-го объекта по j-му критерию
qij ab – абсолютное значение j-го критерия для i-го объекта
qi min , qj max – минимальное и максимальное значение j-го критерия
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем
Оценка: 0.8 0.5 0.75
В случае если чем абсолютное значение больше, тем оценка ниже:
Оценка: 0.25 0.75 0.5

Нормирование
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем

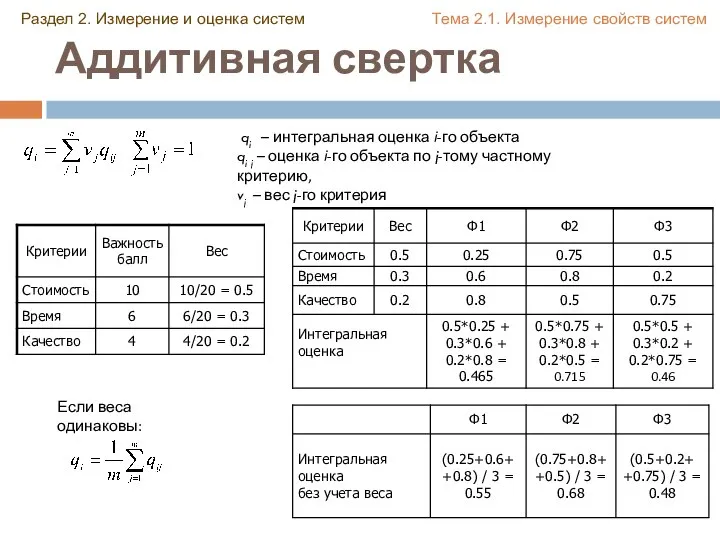
Аддитивная свертка
qi – интегральная оценка i-го объекта
qi j – оценка i-го объекта по j-тому частному критерию,
vj – вес j-го критерия
Если веса одинаковы:
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем

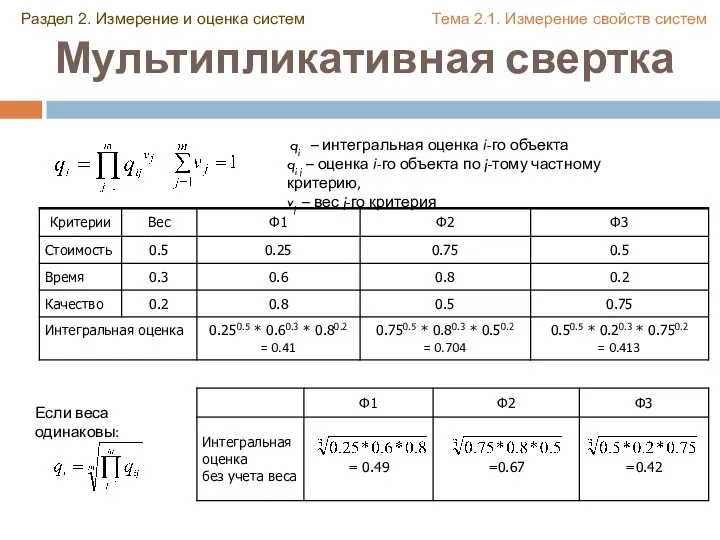
Мультипликативная свертка
Если веса одинаковы:
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем
qi – интегральная оценка i-го объекта
qi j – оценка i-го объекта по j-тому частному критерию,
vj – вес j-го критерия

Метод идеальной точки
Раздел 2. Измерение и оценка систем
Тема 2.1. Измерение свойств систем

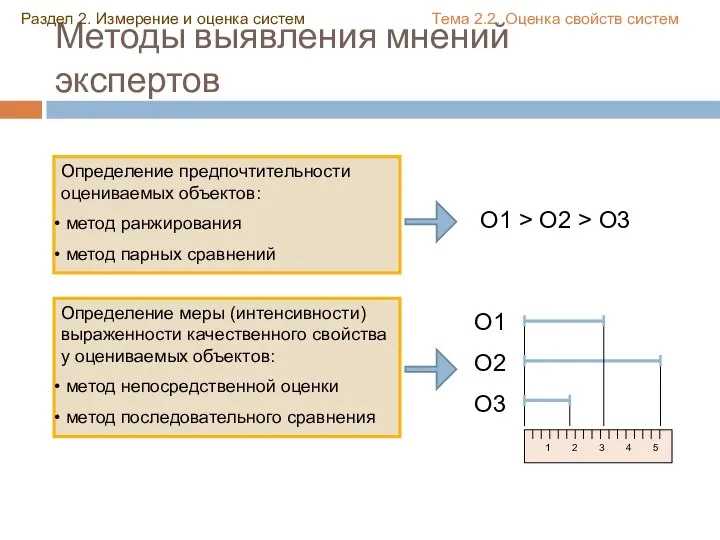
Методы выявления мнений экспертов
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
Определение предпочтительности оцениваемых объектов:
метод ранжирования
метод парных сравнений
Определение меры (интенсивности) выраженности качественного свойства у оцениваемых объектов:
метод непосредственной оценки
метод последовательного сравнения
О1 > O2 > O3
О1
O2
O3

Ранжирование
Эксперт присваивает объектам ранги в порядке предпочтения
Пример ранжирования объектов О1, О2 и О3 разными экспертами:
Для обобщения мнений экспертов - метод суммы мест:
обобщенные ранги присваиваются в соответствии с возрастанием сумм рангов (по всем экспертам).
Эквивалентным объектам дают одинаковые ранги, равные среднеарифметическому значению присваиваемых им рангов.
Такие ранги называют связанными
Сумма: 8 6.5 3.5
Обобщенный 3 2 1
ранг
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
О2 = О3 Ранги: (1 + 2) / 2 = 1.5

Согласованность оценок экспертов
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
Для оценки согласованности мнений экспертов - коэффициент конкордации:
m – количество экспертов,
n – количество объектов,
- оценка мат. ожидания
– показатель связанных рангов в s-й ранжировке
hk – число равных рангов в k-й группе связанных рангов

Согласованность оценок экспертов
Оценка мат. ожидания:
m – количество экспертов
n – количество объектов
Мат. ожидание: ( 8 + 6.5 + 3.5 ) / 3 = 6
Сумма
показателей связанных рангов
hk – число равных рангов в k-й группе связанных рангов
HS = 1, h1 = 2
Т = ТS = 23 - 2 = 6
K = (12 * 10.5) / (32 * (33 – 3) – 3*6) =
= 126 / (9 * 24 – 18) = 126 / 198 = 0.63
0.5 < K < 0.7 – заметная согласованность
Коэффициент конкордации
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
Отклонения от мат. ожидания:
Отклонения: (8-6)2 + (6.5-6)2 + (3.5-6)2 = 10.5

Метод парных сравнений
Эксперт сравнивает каждую пару объектов.
Результаты сравнения - в виде матрицы:
Матрица должна быть согласована:
wii = 1 (по диагонали - 1);
если wij = 1, то wji = 0; (если строгий порядок)
если wij = 1 и wjk = 1, то wik = 1.
Сумма элементов матрицы по столбцу дает ранг объекта от наилучшего к худшему
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
Сравниваем объекты O1, О2, О3
О1 > О2, О1 > О3, О2< О1, О2< O3, O3
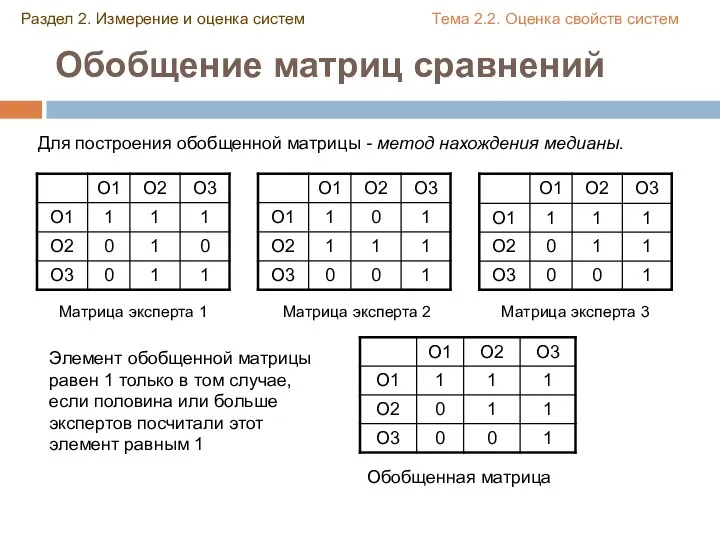
O2

Обобщение матриц сравнений
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
Для построения обобщенной матрицы - метод нахождения медианы.
Обобщенная матрица
Элемент обобщенной матрицы равен 1 только в том случае, если половина или больше экспертов посчитали этот элемент равным 1
Матрица эксперта 1
Матрица эксперта 2
Матрица эксперта 3

Другие методы парных сравнений
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
Превосходство i-го объекта над j-тым измеряется в баллах от 1 до 9:
1 – нет превосходства,
9 – максимальная степень превосходства.
Для согласованности матрицы выполняется:
wi j = 1/wj i ,
т.е. симметричные клетки матрицы заполняются обратными величинами.

Непосредственная оценка
Эксперт присваивает объектам числовые значения, отражающие оценку измеряемого свойства.
Обобщенные оценки строятся с помощью методов осреднения:
aij – оценка i-го объекта j-ым экспертом, m – количество экспертов
Это могут быть:
баллы по 5-, 10-, 100-балльной шкале;
оценки от 0 до 1;
лингвистические значения - «плохо (0.25)», «хорошо (0.75)», «отлично (1.0)» и т.д.
Обобщенная оценка 0.82 0.64 0.58
kj - коэффициенты компетентности экспертов
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем

Последовательное сравнение
(метод Черчмена-Акоффа)
Это комплексный метод, включающий как ранжирование, так и непосредственную оценку.
Допущения:
каждому объекту (варианту решения) oi соответствует действительное неотрицательное число ui, рассматриваемое как мера значимости (полезности);
если oi лучше oj, то ui > uj, если oi эквивалентен oj, то ui = uj;
совместная значимость oi и oj равна (ui + uj);
если значимость ok больше совместной значимости oi и oj , то uk > (ui + uj).
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
Метод может применяться, если допущения выполняются.
Пример, когда допущения не выполняются:
если сравниваемые варианты несовместимы, т.е. не могут наблюдаться одновременно

Алгоритм метода последовательного сравнения
Ранжирование объектов от наиболее предпочтительного объекта к наименее предпочтительному: О1 > О2 > О3 > …> Оn
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
Корректировка оценок , выставленных на шаге 2, так, чтобы они удовлетворяли построенным на шаге 3 неравенствам (начиная с последнего неравенства).
…
3.n-2. Оn-2 >= On-1+On?
3.2. О2 >= О3+О4+ …+ Оn? Да – переход на шаг 3.3
О2 >= О3+О4+ …+ Оn-1? Да – переход на шаг 3.3
…
О2 >= О3+О4?
Сравнение каждого объекта, начиная с О1, лучше ли он комбинации остальных объектов:
3.1. О1 >= О2+О3+ …+ Оn? Да – переход на шаг 3.2
О1 >= О2+О3+ …+ Оn-1? Да – переход на шаг 3.2
…
О1 >= О2+О3?
Непосредственная оценка объектов. Может использоваться шкала от 0 до 1 или от 1 до 10.

Пример применения метода последовательного сравнения
Ранжирование объектов : О1 > О2 > О3 > О4 > О5
Непосредственная оценка: О1 =7, О2 =4, О3 =2, О4 =1.5, О5 =1
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
Итоговые оценки: О1 =8.5, О2 =5, О3 =3, О4 =1.5, О5 =1
(1) О1 < О2+О3 +О4 + О5 8.5 < (5+3+1.5+1)? Да. Не корректируем
(2) О1 < О2+О3+ О4 8.5 < (5+3+1.5)? Да. Не корректируем
(3) О1 > О2+О3 7 > (5 +3)? Нет. Корректируем: О1 =8.5
(4) О2 < О3+О4+О5 5 < (3+1.5+1)? Да. Не корректируем
(5) О2 > О3+О4 4 > (3+1.5)? Нет. Корректируем: О2 =5
Корректировка оценок, начиная от (6), заканчивая (1):
(6) О3 > О4+О5 2 > (1.5+1)? Нет. Корректируем: О3 =3
3.3. О3 >= O4+O5 ? Да: О3 > О4+О5 (6)
3.2. О2 >= О3+О4+О5 ? Нет: О2 < О3+О4+О5 (4)
О2 >= О3+О4 ? Да: О2 > О3+О4 (5)
3. Сравнение каждого объекта с комбинацией остальных объектов:
3.1. О1 >= О2+О3+ О4 + О5? Нет: О1 < О2+О3 +О4 + О5 (1)
О1 >= О2+О3+ О4? Нет: О1 < О2+О3+ О4 (2)
О1 >= О2+О3? Да: О1 > О2+О3 (3)

Организация экспертизы
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
В случае невозможности объективных измерений используются экспертные методы оценивания систем.
Этапы проведения экспертизы:
Постановка проблемы, определение цели экспертизы
Разработка процедуры проведения экспертизы
Формирование группы экспертов
Проведение опроса экспертов
Обработка мнений экспертов, обобщение мнений
Интерпретация результатов экспертизы

Оценка качеств эксперта
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
Способы оценки качеств эксперта:
Априорные методы (не используется информация о результатах участия эксперта в предшествующих экспертизах):
анкетный метод – используются объективные характеристики, имеющие документальное подтверждение (стаж работы, ученая степень, ученое звание, количество публикаций, индекс цитирования)
метод списка (разновидность метода взаимной оценки) - каждый эксперт составляет список компетентных специалистов. Коэффициент компетентности – отношение числа списков, в которых эксперт присутствует, к общему числу списков;
взаимная оценка – эксперты оценивают друг друга.
самооценка - эксперт сам оценивает свои качества по некоторой шкале;

Оценка качеств эксперта
Раздел 2. Измерение и оценка систем
Тема 2.2. Оценка свойств систем
Апостериорные методы (используется информация о результатах участия эксперта в предшествующих экспертизах):
Тестовые методы (эксперт выполняет тестовые задания).
Правильные ответы на вопросы теста (например, значения оцениваемых параметров) должны быть известны аналитической группе, проводящей тест и должна быть разработана шкала для определения точности оценок, даваемых экспертом.
метод оценки достоверности – определяется относительная частота случаев, когда мнение эксперта подтвердилось (например, прогноз)
метод отклонения от групповой оценки – рассчитывается коэффициент отклонения, как отношение отклонения индивидуальной оценки эксперта от результирующей групповой оценки к максимально возможному отклонению;

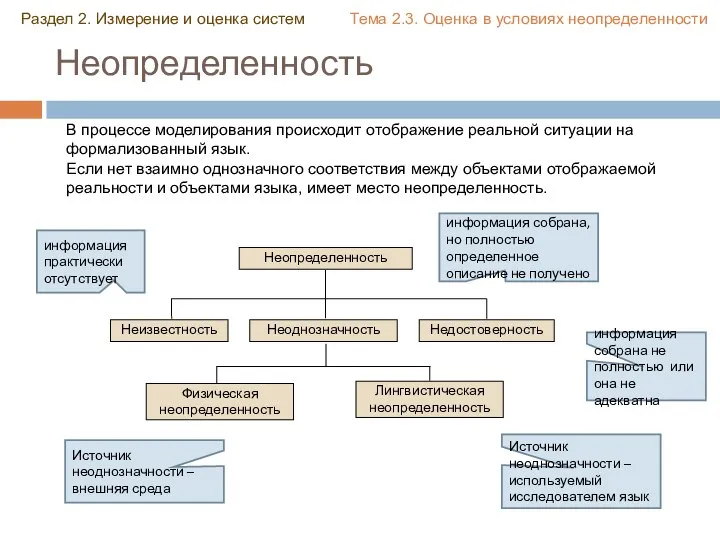
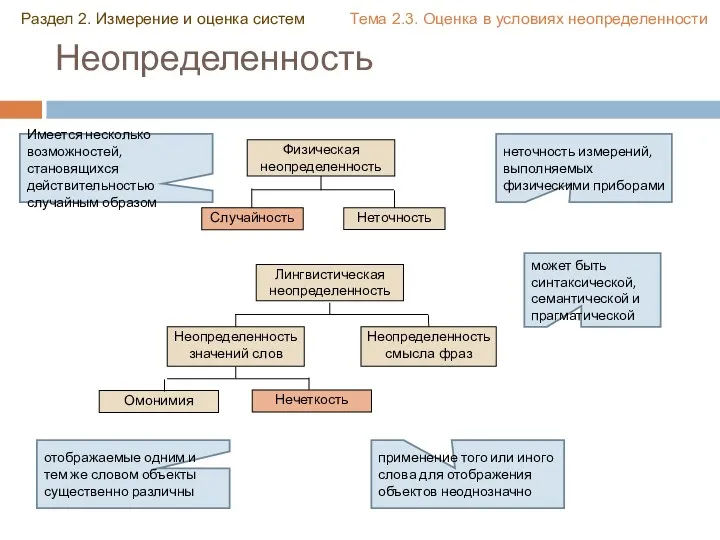
Неопределенность
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
информация практически
отсутствует
информация собрана не полностью или она не адекватна
информация собрана, но полностью определенное описание не получено
Источник неоднозначности – внешняя среда
Источник неоднозначности – используемый исследователем язык
В процессе моделирования происходит отображение реальной ситуации на формализованный язык.
Если нет взаимно однозначного соответствия между объектами отображаемой реальности и объектами языка, имеет место неопределенность.

Неопределенность
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
неточность измерений, выполняемых физическими приборами
Имеется несколько возможностей, становящихся действительностью случайным образом
может быть синтаксической, семантической и прагматической
отображаемые одним и тем же словом объекты существенно различны
применение того или иного слова для отображения объектов неоднозначно

При оценке и выборе вариантов управления нужно учитывать риск – неопределенность состояния внешней среды.
Себестоимость изделий – 10 руб., цена продажи – 50 руб.
Критерий: прибыль = доход – затраты = (цена изделия * кол-во покупателей) –
(себестоимость * кол-во изделий)
Если кол-во изделий > кол-ва клиентов, то кол-во покупателей = кол-ву клиентов
Если кол-во изделий < кол-ва клиентов, то кол-во покупателей = кол-ву изделий
Выбор управления в условиях риска
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
Пример. Изготовление и продажа изделий
50* 5 –10*10 = 150
50*10 –10*10 = 400
50*10 –10*10 = 400
50*10 –10*10 = 400
50*5 – 10*20 = 50
50*15 –10*20 = 550
50*20 –10*20 = 800
50*20 –10*20 = 800
50*5 – 10*30 = 0
50*15 –10*30 = 450
50*25 –10*30 = 950
50*30 –10*30 = 1200

Выбор управления в условиях риска
Критерий среднего выигрыша
Ki – общая эффективность ui
kij – эффективность ui для состояния среды wj
pj – вероятность состояния среды wj
Веро- 0.3 0.4 0.2 0.1
ятность
150*0.3 + 400*0.4 + 400*0.2 + 400*0.1 =325
50*0.3 + 550*0.4 + 800*0.2 + 800*0.1 =475
0*0.3 + 450*0.4 + 950*0.2 + 1200*0.1 =490
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
uopt = u3

Выбор управления в условиях риска
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
Критерий Лапласа
О состояниях среды ничего не известно, поэтому их можно считать равновероятными
(150 + 400 + 400 + 400) / 4 = 337.5
(50 +550 + 800 + 800) / 4 = 550
(0 + 450 + 950 + 1200) / 4 = 650
uopt = u3

Выбор управления в условиях риска
Критерий Вальда (максимина)
min =150
min = 50
min = 0
Критерий Вальда
max = 400
max = 800
max = 1200
Критерий максимакса
Критерий максимакса
Это критерий, осторожного наблюдателя.
Он гарантирует определенный выигрыш при наихудших условиях
ЛПР надеется на лучшее состояние среды и в большой степени рискует
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
uopt = u1
uopt = u3

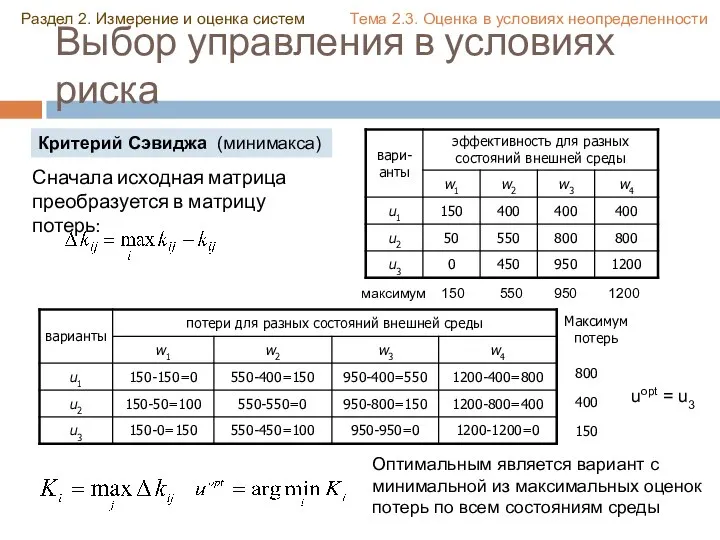
Выбор управления в условиях риска
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
Критерий Гурвица (пессимизма-оптимизма)
коэффициент
оптимизма
При α = 0 - критерий Вальда
при α = 1 – критерий максимакса
Результат зависит от отношения к риску ЛПР
0.6*400 + (1-0.6)* 150 = 300
0.6*800 + (1-0.6)* 50 = 500
0.6*1200 + (1-0.6)* 0 = 720
Коэффициент оптимизма
α = 0.6
uopt = u3

Выбор управления в условиях риска
Сначала исходная матрица преобразуется в матрицу потерь:
Оптимальным является вариант с минимальной из максимальных оценок потерь по всем состояниям среды
800
400
150
Максимум потерь
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
Критерий Сэвиджа (минимакса)
uopt = u3
максимум 150 550 950 1200

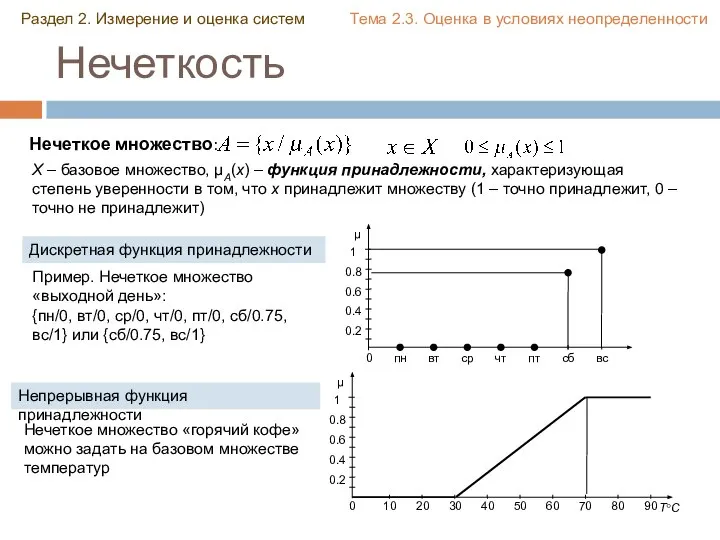
Нечеткость
Нечеткое множество:
X – базовое множество, µA(x) – функция принадлежности, характеризующая степень уверенности в том, что x принадлежит множеству (1 – точно принадлежит, 0 – точно не принадлежит)
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
Пример. Нечеткое множество «выходной день»:
{пн/0, вт/0, ср/0, чт/0, пт/0, сб/0.75, вс/1} или {сб/0.75, вс/1}
Нечеткое множество «горячий кофе» можно задать на базовом множестве температур
Дискретная функция принадлежности
Непрерывная функция принадлежности

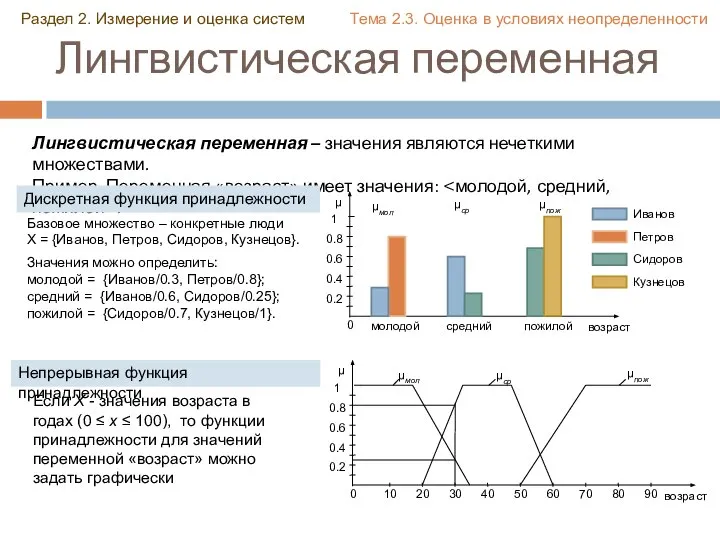
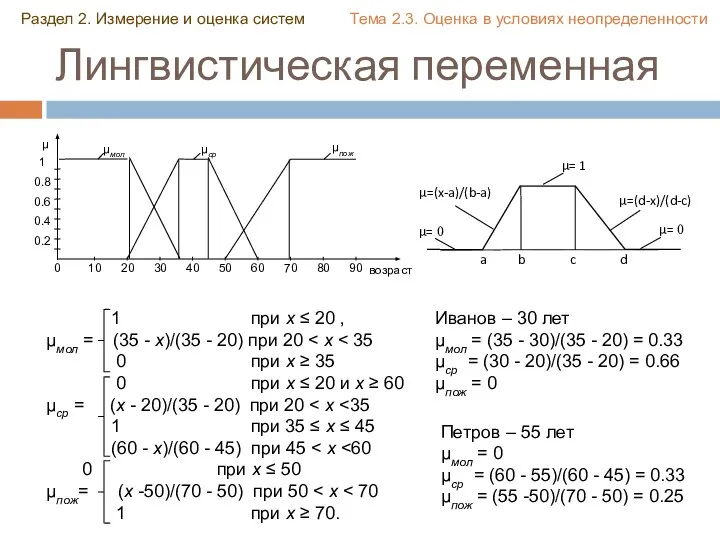
Лингвистическая переменная
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
Лингвистическая переменная – значения являются нечеткими множествами.
Пример. Переменная «возраст» имеет значения: <молодой, средний, пожилой>.
Базовое множество – конкретные люди
Х = {Иванов, Петров, Сидоров, Кузнецов}.
Значения можно определить:
молодой = {Иванов/0.3, Петров/0.8};
средний = {Иванов/0.6, Сидоров/0.25};
пожилой = {Сидоров/0.7, Кузнецов/1}.
Если X - значения возраста в годах (0 ≤ x ≤ 100), то функции принадлежности для значений переменной «возраст» можно задать графически
Дискретная функция принадлежности
Непрерывная функция принадлежности

Лингвистическая переменная
1 при х ≤ 20 ,
μмол = (35 - x)/(35 - 20) при 20 < x < 35
0 при х ≥ 35
0 при х ≤ 20 и х ≥ 60
μср = (х - 20)/(35 - 20) при 20 < x <35
1 при 35 ≤ х ≤ 45
(60 - x)/(60 - 45) при 45 < x <60
0 при х ≤ 50
µпож= (x -50)/(70 - 50) при 50 < x < 70
1 при х ≥ 70.
Иванов – 30 лет
μмол = (35 - 30)/(35 - 20) = 0.33
μср = (30 - 20)/(35 - 20) = 0.66
µпож = 0
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
Петров – 55 лет
μмол = 0
μср = (60 - 55)/(60 - 45) = 0.33
µпож = (55 -50)/(70 - 50) = 0.25

Нечеткие логические операции
Пересечением нечетких множеств A и B является наибольшее нечеткое множество, содержащееся одновременно в A и B, с функцией принадлежности:
Объединением нечетких множеств A и B является наименьшее нечеткое множество, включающее как A, так и B, с функцией принадлежности:
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности
Пример. Нечеткое множество «небольшое натуральное число»:
{1/1.0, 2/1.0, 3/0.9, 4/0.8, 5/0.6, 6/0.5, 7/0.4, 8/0.2, 9/0.1}
Нечеткое множество «число, приблизительно равное 2»:
{1/0.5, 2/1.0, 3/0.6, 4/0.4, 5/0.2, 6/0}
Нечеткое множество «небольшое натуральное число, приблизительно равное 2»:
{1/0.5, 2/1.0, 3/0.6, 4/0.4, 5/0.2, 6/0}

Нечеткая логика
Нечеткое высказывание U – логическое высказывание, для которого задано отображение истинности T: U → [0, 1].
Пример: Т(«Иванов - высокий») = 0.7
Конъюнкция нечетких высказываний:
Дизъюнкция нечетких высказываний:
Если Т(«Иванов - высокий») = 0.7, Т(«Иванов - молодой») = 0.5, то
Т(«Иванов - высокий» И «Иванов - молодой») = min (0.7, 0.5) = 0.5
Раздел 2. Измерение и оценка систем
Тема 2.3. Оценка в условиях неопределенности