П О Р Т ФО Л И О п р о е к т а " Т реугольники"

Определение:
Треугольник можно построить по трём точкам, не лежащим на одной прямой.
Классификационная схема видов треугольников:
по углам: остроугольный, прямоугольный, тупоугольный.
по сторонам: разносторонний, равнобедренный, равносторонний.
Треугольник.
Основные понятия и элементы.

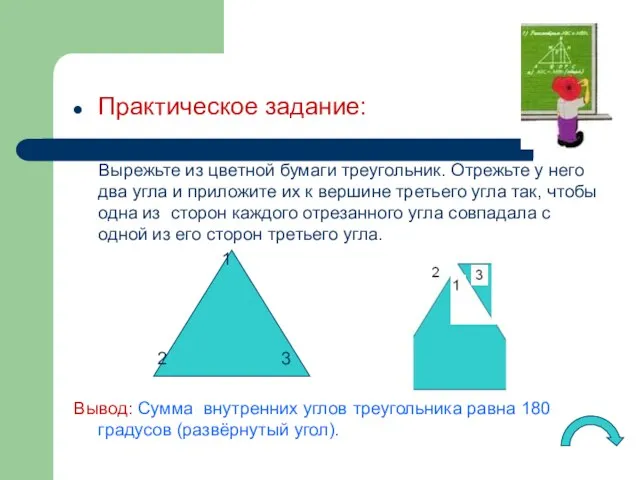
Практическое задание:
Вырежьте из цветной бумаги треугольник. Отрежьте у него два угла и приложите их к вершине третьего угла так, чтобы одна из сторон каждого отрезанного угла совпадала с одной из его сторон третьего угла.
1
2 3
Вывод: Сумма внутренних углов треугольника равна 180 градусов (развёрнутый угол).

Практическая задача:
Столяру нужно заделать отверстие треугольной формы. Сколько и каких мерок он должен снять, чтобы изготовить подходящую латку, если отверстие имеет форму:
а) прямоугольного треугольника;
б) равностороннего треугольника;
в) равнобедренного треугольника;
г) разностороннего треугольника.
Решение:
а) три стороны и два угла;
б) одну сторону и один угол;
в) две стороны и два угла;
г) три стороны и три угла.

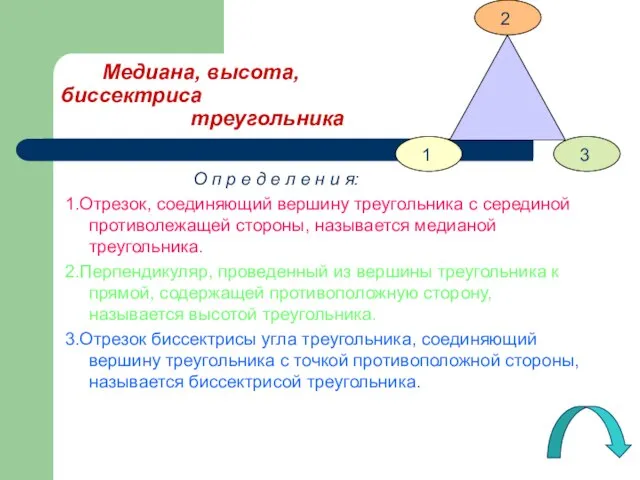
Медиана, высота, биссектриса
треугольника
О п р е д е л е н и я:
1.Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой треугольника.
2.Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
3.Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

Практическое задание:
а) Вырежьте из бумаги треугольники: Остроугольный, прямоугольный, тупоугольный, равнобедренный и равносторонний. Для каждого сгибанием постройте по три медианы. Линии сгиба выделите разными цветами.
б) Вырежьте из бумаги треугольники: Остроугольный, прямоугольный, тупоугольный, равнобедренный и равносторонний. Для каждого сгибанием постройте по три биссектрисы. Линии сгиба выделите разными цветами.
в) Вырежьте из бумаги треугольники: Остроугольный, прямоугольный, тупоугольный, равнобедренный и равносторонний. Для каждого сгибанием постройте по три высоты. Линии сгиба выделите разными цветами. ВО всех ли случаях можно построить высоты путем сгибания треугольника?
СДЕЛАЙ САМ!

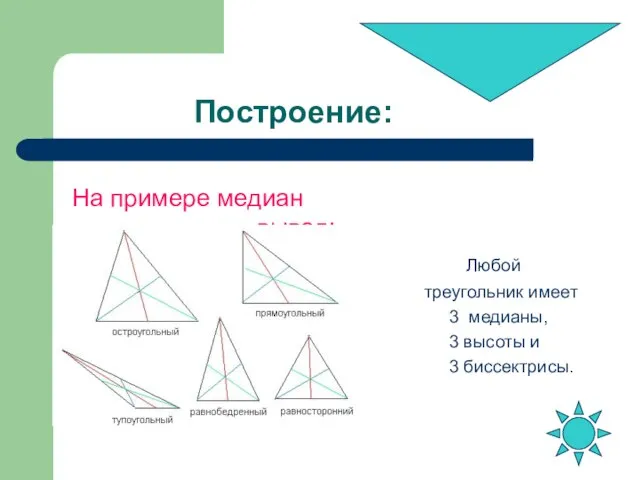
Построение:
На примере медиан вывод:
Любой
треугольник имеет
3 медианы,
3 высоты и
3 биссектрисы.

Существуют три признака равенства треугольников.
Проблемные вопросы и ответы на них:
1.Верно ли, что все равносторонние треугольники равны между собой? НЕТ
2. При наложении у треугольников совпадали одна сторона и один угол. Можно ли утверждать, что треугольники равны? НЕТ
3.При наложении у треугольников две стороны и один угол. Можно ли утверждать, что треугольники равны? ДА
4.При наложении у треугольников
совпали два угла и одна сторона.
Можно ли утверждать,
что треугольники равны?
ДА
Признаки равенства треугольников.

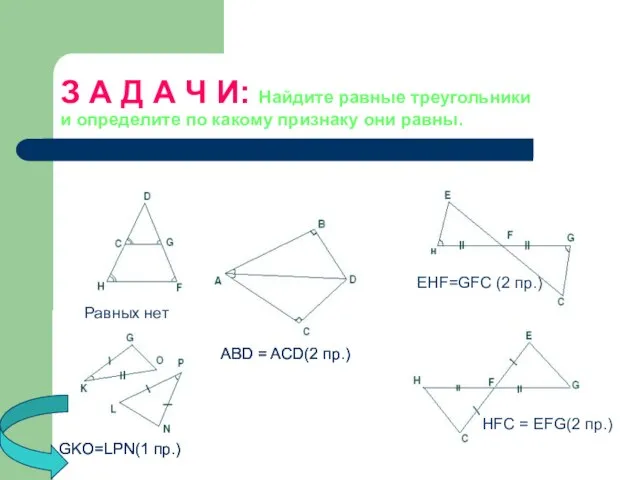
З А Д А Ч И: Найдите равные треугольники
и определите по какому признаку они равны.
GKO=LPN(1 пр.)
GKO=LPN(1 пр.)
EHF=GFC (2 пр.)
HFC = EFG(2 пр.)
ABD = ACD(2 пр.)
ABD = ACD(2 пр.)
Равных нет

Практическая задача
Мама купила кусок ткани размером 1м ∙ 1м на платки двум дочерям. Помогите ей разделить этот кусок на две равные части с помощью одного прямолинейного разреза. Укажите всевозможные способы разрезания и обоснуйте правильность своих действий.
Решение: При таком разрезе, платки получились равными.

Определение: Треугольник, две стороны которого равны, называется равнобедренным.
Проблемные вопросы и ответы к ним.
Равнобедренный треугольник
1.Верно ли, что у равнобедренного треугольника только две стороны равны? ДА
2. Верно ли, что у равнобедренного треугольника только два угла равны? ДА
3.Как вырезать равнобедренный треугольник из прямоугольного листа бумаги, если можно сделать один разрез ножницами?(Бумагу можно предварительно сгибать)

Обозначьте буквами изображенный на рисунке прямоугольник и все проведенные отрезки. Найдите на рисунке все прямоугольные треугольники и укажите среди них равные между собой.
BFQ, BYQ, QYC, AFQ,
AHQ, PNQ, QHD, QND,
DIT, QNT, ABC, ADC
ЗАДАЧА:
Прямоугольный треугольник