Содержание
- 2. Почему мы взялись за эту работу? Мы очень любим решать задачи и разгадывать математические ребусы, но
- 3. Почему мы взялись за эту работу? Поиск заключенных в софизме ошибок, ясное понимание их причин ведут
- 4. Цель и задачи. Цель: изучить данную тему и создать презентацию для использования ее на уроках. Задачи:
- 5. В Древней Греции «софисты» (от греческого слова sofos, означающего мудрость) – мыслители, люди, авторитетные в различных
- 6. Софизм- формально кажущееся правильным, но по существу ложное умозаключение, основанное на неправильном подборе исходных положений (словарь
- 7. Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.
- 8. числовые геометрические алгебраические логические В своей работе мы рассмотрели много математических софизмов и сейчас приведем примеры
- 9. Софизм №1 «Пять равно шести» Возьмем тождество 35+10-45=42+12-54. В каждой части вынесем за скобки общий множитель:
- 10. Известно, что любые два равенства можно перемножить почленно, не нарушая при этом равенства, т. е.если а
- 11. Разбор софизма: Ошибка, допущенная в этом софизме, состоит в нарушении правила действий с именованными величинами: все
- 12. Софизм №3 «Дважды два - пять» Напишем тождество 4:4=5:5. Вынесем из каждой части тождества общие множители
- 13. Софизм №4 «Уравнение x-a=0 не имеет корней» Дано уравнение x-a=0. Разделив обе части этого уравнения на
- 14. Софизм №5 «Полный стакан равен пустому» Пусть имеется стакан, наполненный водой до половины. Тогда можно сказать,
- 15. Логические софизмы «Софизм учебы» Данным софизмом является песенка, сочиненная английскими студентами: Песенка The more you study,
- 16. Перевод. Чем больше учишься, тем больше знаешь. Чем больше знаешь, тем больше забываешь. Чем больше забываешь,
- 17. Парадокс (греч. "пара" - "против", "докса" - "мнение") близок к софизму. Но от него он отличается
- 18. Это парадоксы, которые затрагивают сферы логики и здравого смысла. Казалось бы, парадокс - и парадокс себе,
- 19. Этот древнегреческий логический парадокс имеет множество вариаций. Мы приведем одну из них. Человек произносит: « Я
- 20. Имеется утверждение: разница между "кучей" и "не кучей" не в одном элементе. Возьмем некоторую кучу, например,
- 21. В некой деревне, в которой живет один единственный парикмахер, был издан указ: "Парикмахер имеет право брить
- 22. Если он хочет сам себя брить, то он не может этого сделать, так как он может
- 23. Каждый мэр города живет или в своем городе, или вне него. Был выделен один специальный город,
- 24. Если мэр не пожелает жить в своем городе, то он все равно должен жить в нем,
- 26. Скачать презентацию





















 THE CHRISTIAN WORKER
THE CHRISTIAN WORKER 1665678763032__30ro86
1665678763032__30ro86 Агрессия (4 класс)
Агрессия (4 класс) 1.1 + 1.2
1.1 + 1.2 История носового платка
История носового платка Поля листа
Поля листа Вкусное и красивое лакомство для неожиданных гостей
Вкусное и красивое лакомство для неожиданных гостей Добро пожаловать
Добро пожаловать Независимое распределение затрат в управленческом и регламентированном учете
Независимое распределение затрат в управленческом и регламентированном учете Абсолютные показатели оценки риска
Абсолютные показатели оценки риска Кипение
Кипение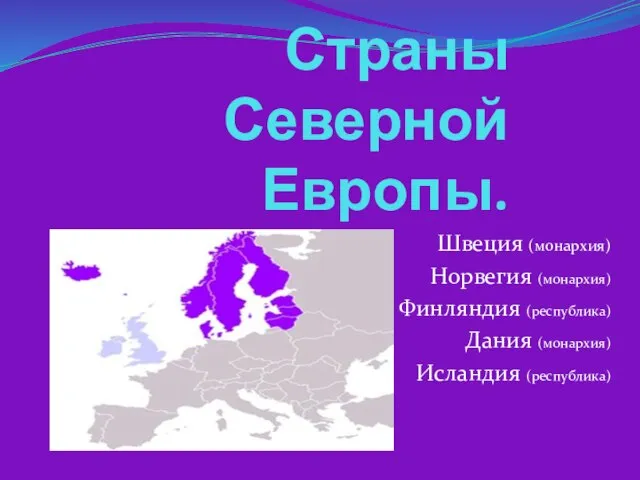 Страны Северной Европы
Страны Северной Европы Конструкция головы человека и её пропорции (6 класс)
Конструкция головы человека и её пропорции (6 класс) Энтеровирусная инфекция
Энтеровирусная инфекция Конвекция
Конвекция САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ Ассоциация «МЫ»
Ассоциация «МЫ»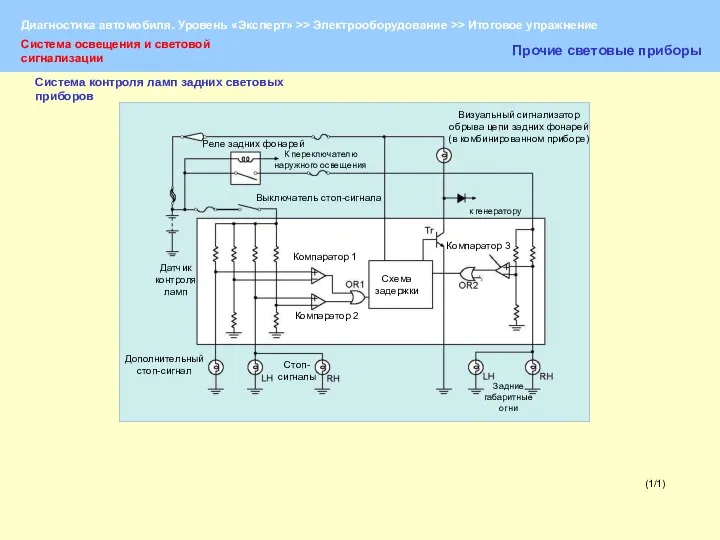 Диагностика автомобиля. Диагностирование осветительных приборов
Диагностика автомобиля. Диагностирование осветительных приборов Денис Васильевич Давыдов
Денис Васильевич Давыдов Рекомендую как пособие по медицинской генетике
Рекомендую как пособие по медицинской генетике Любимый семейный завтрак семьи Пьянковых
Любимый семейный завтрак семьи Пьянковых Доброта
Доброта О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ
О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ Психологические закономерности формирования личности в тренировочном процессе.
Психологические закономерности формирования личности в тренировочном процессе. Базовый межшкольный методический центр 26311
Базовый межшкольный методический центр 26311 Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс Выявление и устройство детей-сирот и детей оставшихся без попечения родителей.
Выявление и устройство детей-сирот и детей оставшихся без попечения родителей. Создание единого китайского государства
Создание единого китайского государства