Парная регрессия и корреляция в эконометрических исследованиях. Смысл и оценка параметров

Экономический смысл ε
Невключение объясняющих переменных в уравнение. На самом деле на переменную Y влияет не только переменная X, но и ряд других переменных, которые не учтены в модели по следующим причинам:
мы знаем, что другая переменная влияет, но не можем ее учесть, потому как не знаем, как измерить (психологический фактор, например);
существуют факторы, которые мы знаем, как измерить, но влияние их на Y так слабо, что их не стоит учитывать;
существенные переменные, но из-за отсутствия опыта или знаний мы их таковыми не считаем.
Неправильная функциональная спецификация. Функциональное соотношение между Y и Х может быть определено неправильно. Например, мы предположили линейную зависимость, а она может быть более сложной.
Ошибки наблюдений и измерений.

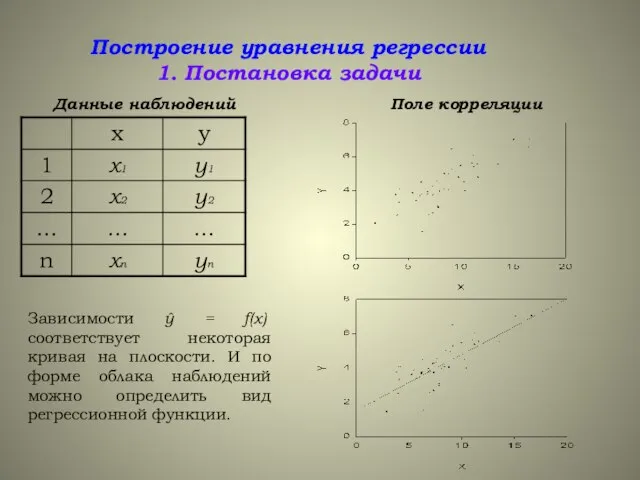
Построение уравнения регрессии
1. Постановка задачи
Данные наблюдений
Поле корреляции
Зависимости ŷ = f(x) соответствует некоторая кривая на плоскости. И по форме облака наблюдений можно определить вид регрессионной функции.

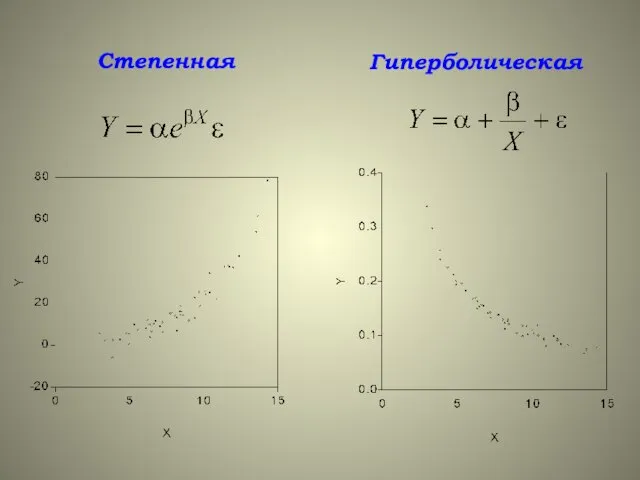
Степенная
Гиперболическая

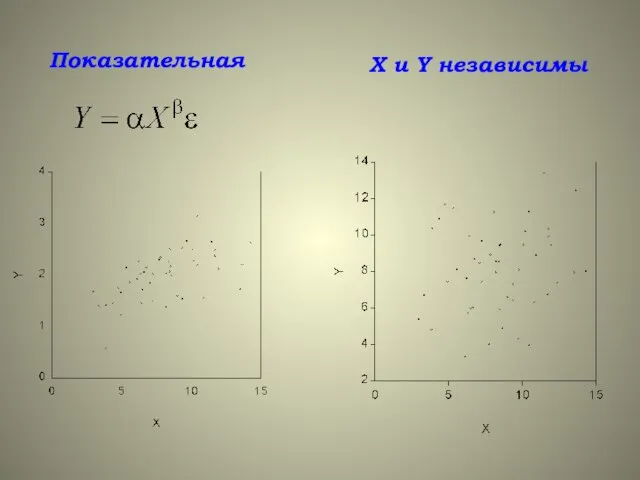
Показательная
X и Y независимы

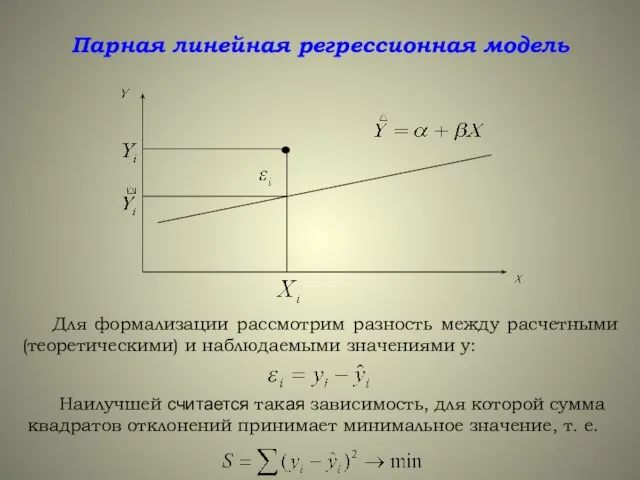
Парная линейная регрессионная модель
Для формализации рассмотрим разность между расчетными (теоретическими) и наблюдаемыми значениями у:
Наилучшей считается такая зависимость, для которой сумма квадратов отклонений принимает минимальное значение, т. е.

2. Спецификация модели
В парной регрессии выбор вида аналитической зависимости может быть осуществлен тремя методами:
– графическим (на основе анализа поля корреляции);
– аналитическим (на основе изучения теоретической природы связи между исследуемыми признаками);
– экспериментальным (построение нескольких моделей различного вида с выбором наилучшей, согласно применяемому критерию качества).

3. Оценка параметров модели
3.1. Оценка параметров линейной парной регрессии – метод наименьших квадратов (МНК)
или
Отсюда получаем систему уравнений:
Разделим оба уравнения на n:
Подставляем во второе уравнение:

3.2. Оценка параметров нелинейных моделей

1. Задаются некоторые «правдоподобные» начальные (исходные) значения параметров а и b.
2. Вычисляются теоретические значения ŷi = f(xi) с использованием этих значений параметров.
3. Вычисляются остатки еi = ŷi – yi и сумма квадратов остатков S.
4. Вносятся изменения в одну или более оценку параметров.
5. Вычисляются новые теоретические значения ŷi, остатки еi и S.
6. Если произошло уменьшение S, то новые значения оценок используются в качестве новой отправной точки.
7. Шаги 4, 5 и 6 повторяются до тех пор, пока не будет достигнута ситуация, когда величину S невозможно будет улучшить (в пределах заданной точности).
8. Полученные на последнем шаге значения параметров а и b являются оценками параметров нелинейного уравнения регрессии.
Оценка параметров внутренне нелинейных моделей:

4. Проверка качества уравнения регрессии
Н0: уравнение статистически не значимо
yi = ŷi + εi
D(y) = D(ŷ) + D(ε)

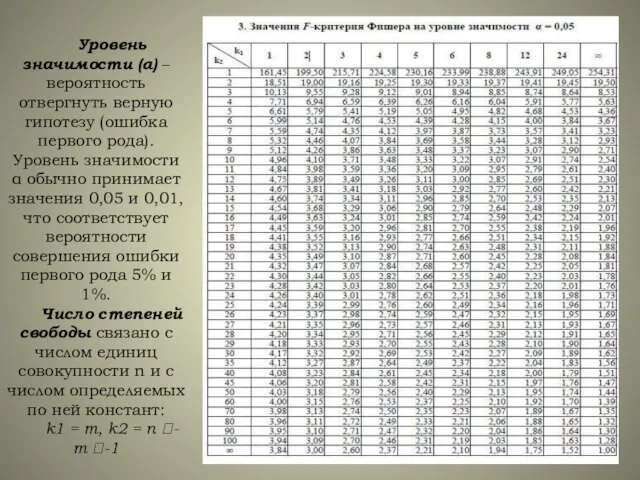
F-критерий Фишера:
где m – число независимых переменных в уравнении регрессии (для парной регрессии m = 1);
n – число единиц совокупности.
Если Fфакт > Fтабл, то Н0 о случайной природе связи отклоняется и признается статистическая значимость и надежность уравнения.
Если Fфакт < Fтабл, то Н0 не отклоняется и признается статистическая незначимость уравнения регрессии.

Уровень значимости (α) – вероятность отвергнуть верную гипотезу (ошибка первого рода). Уровень значимости α обычно принимает значения 0,05 и 0,01, что соответствует вероятности совершения ошибки первого рода 5% и 1%.
Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант:
k1 = m, k2 = n - m -1

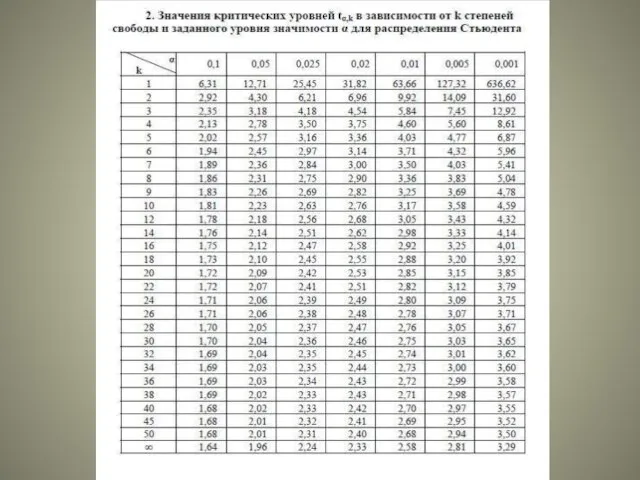
t-критерий Стьюдента
Н0: а=0; b=0
Стандартные ошибки параметров регрессии и коэффициента корреляции:

Оценка значимости параметров уравнения и коэффициента корреляции проводится путем сопоставления их значений с величиной случайной ошибки:
Если tфакт > tтабл, то Н0 отклоняется, т.е. a, b, r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х.
Если tфакт < tтабл, то Н0 не отклоняется и признается случайная природа формирования a, b, r.

Доверительные интервалы – это пределы, в которых лежит точное значение определяемого показателя с заданной вероятностью.
Доверительные интервалы для параметров a и b уравнения линейной регрессии определяются соотношениями:
;