Содержание
- 2. Система счисления – это способ представления чисел в виде определенного набора цифр. Система счисления – это
- 3. Все системы счисления делятся на позиционные и непозиционные. Позиционные системы счисления – это такие системы счисления,
- 4. Основание системы счисления в позиционной системе счисления – это количество цифр в алфавите. Алфавит системы счисления
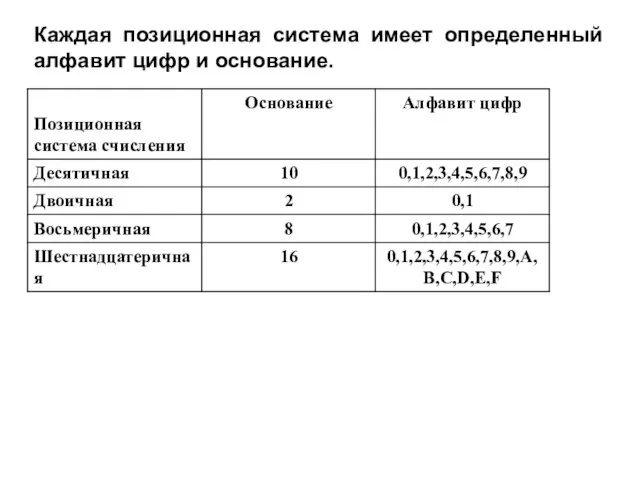
- 5. Каждая позиционная система имеет определенный алфавит цифр и основание.
- 7. Перевод целых десятичных чисел в двоичный код Число 52810 переведем в двоичную систему счисления. Способ 1
- 8. Правило перевода целых десятичных чисел в 2-ю, 8-ю, 16-ю системы счисления (способ 2) 1. Целое десятичное
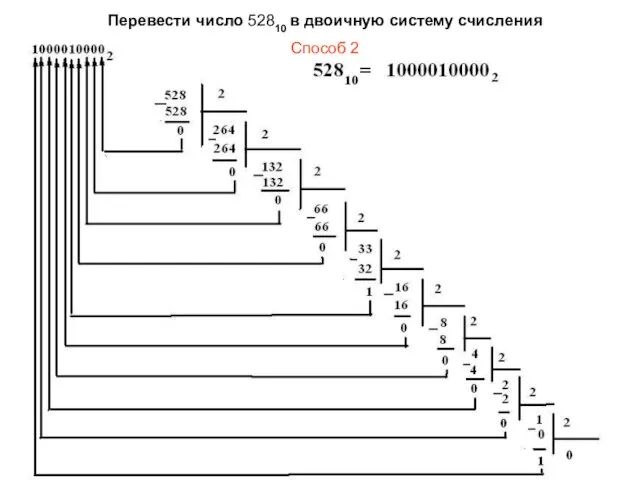
- 9. Перевести число 52810 в двоичную систему счисления Способ 2
- 10. Перевод двоичного числа 10000100002 в десятичный код Двоичный ряд Двоичное число Умножим попарно цифры двоичного числа
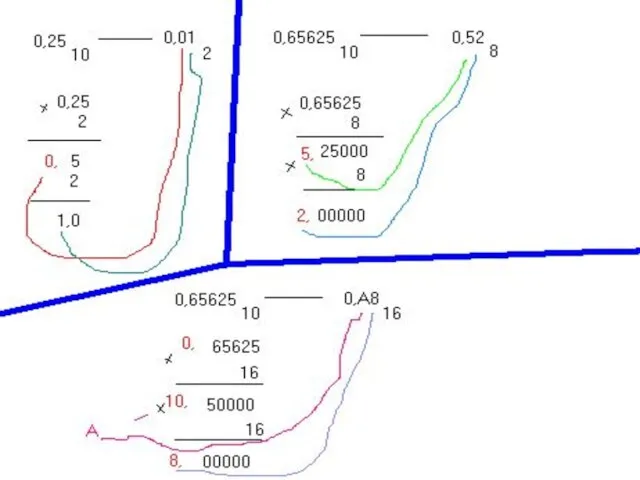
- 11. Правило перевода дробных десятичных чисел в 2-й, 8-й, 16-й коды Дробное десятичное число умножают на основание
- 13. Пример. Перевести число 1011000010001100102 в 8-ю систему счисления. Решение: 1. Разбиваем число справа налево на триады
- 14. Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 8 и обратно
- 15. Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 16 и обратно
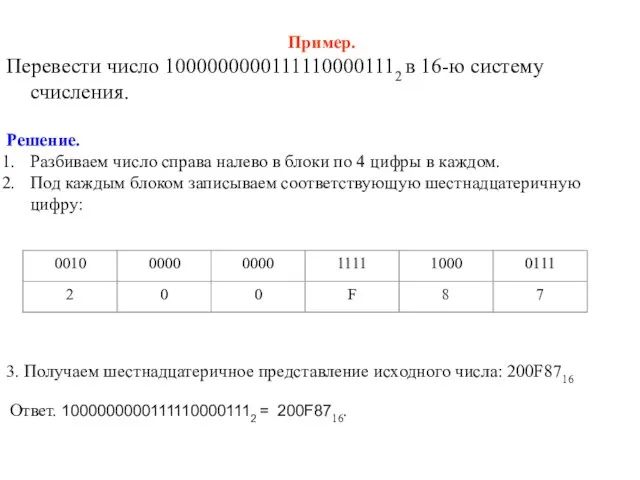
- 16. Пример. Перевести число 10000000001111100001112 в 16-ю систему счисления. Решение. Разбиваем число справа налево в блоки по
- 18. Скачать презентацию










 КРАЕВАЯ ЦЕЛЕВАЯ ПРОГРАММА «РАЗВИТИЕ СЕМЕЙНОЙ ПОЛИТИКИ В ХАБАРОВСКОМ КРАЕ НА 2012-2014 гг.» - ИТОГ ВЗАИМОДЕЙСТВИЯ ВЛАСТИ И ГРАЖДАНСКОГО
КРАЕВАЯ ЦЕЛЕВАЯ ПРОГРАММА «РАЗВИТИЕ СЕМЕЙНОЙ ПОЛИТИКИ В ХАБАРОВСКОМ КРАЕ НА 2012-2014 гг.» - ИТОГ ВЗАИМОДЕЙСТВИЯ ВЛАСТИ И ГРАЖДАНСКОГО Графический дизайн в рекламе. Логотип. Опрос по пройденному материалу
Графический дизайн в рекламе. Логотип. Опрос по пройденному материалу Издержки предприятия и себестоимость продукции. Лекция 6
Издержки предприятия и себестоимость продукции. Лекция 6 Что скрывает живопись автора? Реставрация масляной живописи
Что скрывает живопись автора? Реставрация масляной живописи Презентация ко Дню рыбака (8 июля)
Презентация ко Дню рыбака (8 июля) Рецепты салатов из сырых овощей
Рецепты салатов из сырых овощей ООО СПЕКТР-СПБ. Лакокрасочные материалы при строительстве транспортной инфраструктуры
ООО СПЕКТР-СПБ. Лакокрасочные материалы при строительстве транспортной инфраструктуры Игра как сценарий построения и восприятия рекламы.
Игра как сценарий построения и восприятия рекламы. 20140314_prezentatsiya_microsoft_office_powerpoint_0
20140314_prezentatsiya_microsoft_office_powerpoint_0 LegoCar. Коммерческое предложение по SMM и таргетированной рекламе
LegoCar. Коммерческое предложение по SMM и таргетированной рекламе Подвижные игры
Подвижные игры Витрины. 3 класс
Витрины. 3 класс Решения IBM для розничной торговли
Решения IBM для розничной торговли ОСНОВНЫЕ ПОЛОЖЕНИЯ Закона Калужской области №274-ОЗ
ОСНОВНЫЕ ПОЛОЖЕНИЯ Закона Калужской области №274-ОЗ Расчет параметров цифровых следящих систем, реализованных на FPGA
Расчет параметров цифровых следящих систем, реализованных на FPGA Федеральные государственные требования к планированию содержания раздела «Коррекционная работа при разработке образовательной
Федеральные государственные требования к планированию содержания раздела «Коррекционная работа при разработке образовательной  Средства декорирования поверхности изделий из древесины
Средства декорирования поверхности изделий из древесины DREAM LAND
DREAM LAND Современный Дед Мороз
Современный Дед Мороз Советская культура 1930-х годов
Советская культура 1930-х годов Укрепление материально-технической базы учреждений образования Полоцкого района в 2012 году
Укрепление материально-технической базы учреждений образования Полоцкого района в 2012 году АКУПУНКТУРНАЯ КОРРЕКЦИЯ КОНТРАКТУРЫ МИМИЧЕСКИХ МЫШЦ
АКУПУНКТУРНАЯ КОРРЕКЦИЯ КОНТРАКТУРЫ МИМИЧЕСКИХ МЫШЦ Проект Закона Республики Казахстан «О внесении изменений и дополнений в некоторые законодательные акты Республики Казахстан по
Проект Закона Республики Казахстан «О внесении изменений и дополнений в некоторые законодательные акты Республики Казахстан по  Деление урана
Деление урана Типология социальных групп
Типология социальных групп Таблица Менделеева внутри нас
Таблица Менделеева внутри нас Датировка источника, хронология.
Датировка источника, хронология. Увлажняющие гранулы для ванн «Кураж» - это революционный подход к уходу за телом, косметические соли нового поколения. Они быстро и
Увлажняющие гранулы для ванн «Кураж» - это революционный подход к уходу за телом, косметические соли нового поколения. Они быстро и