Перпендикуляр и наклонная

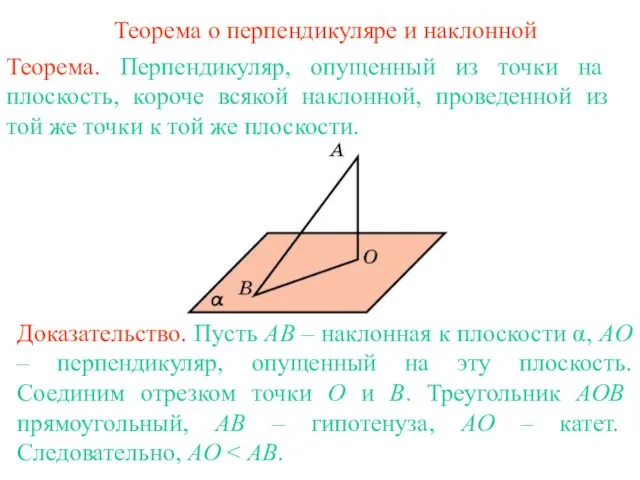
Теорема о перпендикуляре и наклонной
Теорема. Перпендикуляр, опущенный из точки на плоскость, короче всякой наклонной, проведенной из той же точки к той же плоскости.
Доказательство. Пусть AB – наклонная к плоскости α, AO – перпендикуляр, опущенный на эту плоскость. Соединим отрезком точки O и B. Треугольник AOB прямоугольный, AB – гипотенуза, AO – катет. Следовательно, AO < AB.

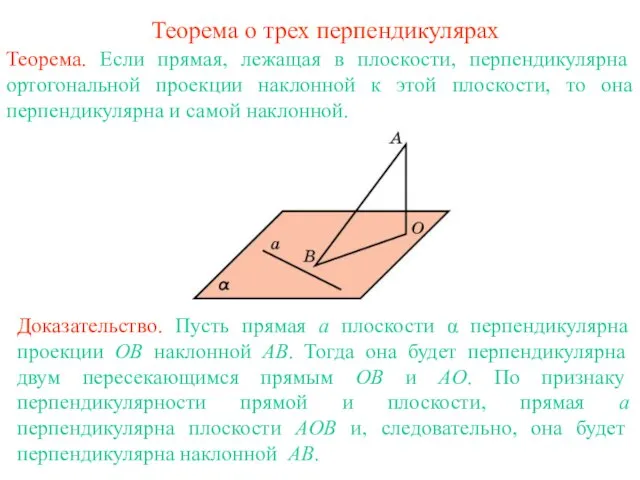
Теорема о трех перпендикулярах
Теорема. Если прямая, лежащая в плоскости, перпендикулярна ортогональной проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной.
Доказательство. Пусть прямая а плоскости α перпендикулярна проекции OB наклонной АВ. Тогда она будет перпендикулярна двум пересекающимся прямым OB и AO. По признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости АOВ и, следовательно, она будет перпендикулярна наклонной АВ.

Верно ли утверждение: «Если из двух различных точек, не принадлежащих плоскости, проведены к ней две равные наклонные, то их проекции тоже равны»?
Ответ: Нет.
Упражнение 1

К плоскости прямоугольника ABCD в точке пересечения диагоналей восстановлен перпендикуляр. Верно ли утверждение о том, что произвольная точка M этого перпендикуляра равноудалена от вершин прямоугольника?
Ответ: Да.
Упражнение 2

Точка M равноудалена от всех точек окружности. Верно ли утверждение о том, что она принадлежит перпендикуляру к плоскости окружности, проведённому через её центр?
Ответ: Да.
Упражнение 3

Найдите ГМ оснований наклонных одинаковой длины, проведённых к данной плоскости из данной точки.
Ответ: Окружность.
Упражнение 4

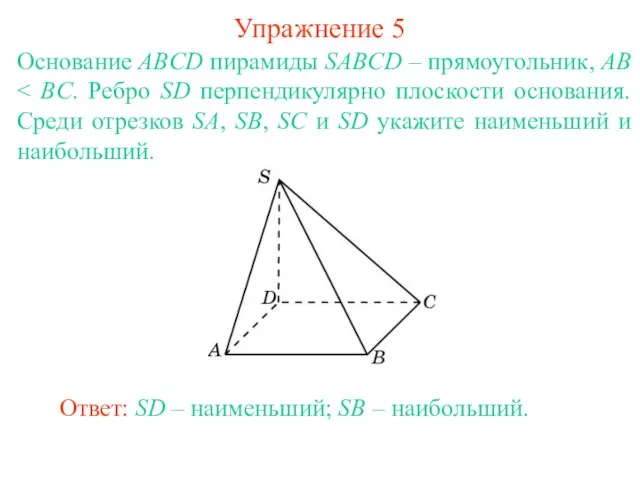
Основание ABCD пирамиды SABCD – прямоугольник, AB < BC. Ребро SD перпендикулярно плоскости основания. Среди отрезков SA, SB, SC и SD укажите наименьший и наибольший.
Ответ: SD – наименьший; SB – наибольший.
Упражнение 5

Из точки A к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках B и C. Найдите проекцию отрезка AC, если AC = 37 см, AB = 35 см.
Ответ: 12 см.
Упражнение 6

Из точки A к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках B и C. Найдите отрезок AC, если AB = 6 см, ∠BAC = 60°.
Ответ: 12 см.
Упражнение 7

Из точки A к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках B и C. Найдите отрезок AB, если AC = см, BC = 3AB.
Ответ: 2 см.
Упражнение 8

Отрезки двух наклонных, проведенных из одной точки к плоскости, равны 15 см и 20 см. Проекция одного из этих отрезков равна 16 см. Найдите проекцию другого отрезка.
Ответ: 9 см.
Упражнение 9

Отрезок BC длиной 12 см является проекцией отрезка AC на плоскость α. Точка D принадлежит отрезку AC и AD:DC = 2:3. Найдите отрезок AD и его проекцию на плоскость α, если известно, что AB = 9 см.
Ответ: 6 см; 4,8 см.
Упражнение 10

Дан прямоугольный треугольник ABC, катеты которого AC и BC равны соответственно 20 и 15 см. Через вершину A проведена плоскость α, параллельная прямой BC. Проекция одного из катетов на эту плоскость равна 12 см. Найдите проекцию гипотенузы.
Упражнение 11

Сторона ромба равна a, острый угол 60°. Через одну из сторон ромба проведена плоскость. Проекция другой стороны на эту плоскость равна b. Найдите проекции диагоналей ромба.
Упражнение 12

Найдите геометрическое место точек в пространстве, равноудаленных от двух данных точек.
Упражнение 13
Ответ: Плоскость, проходящая через середину отрезка, соединяющего данные точки, и перпендикулярная этому отрезку.