Содержание
- 2. Задача Возраст педагогических работников (в годах): 18; 38; 40; 28; 29; 26; 38; 34; 22; 28;
- 3. Меры центральной тенденции Мода (Мо) - значение, которое чаще других встречается в выборке. Если все значения
- 4. Меры центральной тенденции: Мода В интервальном вариационном ряду: 1)Данные уже сгруппированы в интервалы 2) Найти интервал
- 5. Меры центральной тенденции Медиана (Md) - значение признака, которое делит ранжированное множество данных пополам так, что
- 6. Меры центральной тенденции: Медиана В интервальном вариационном ряду: 1) Если данные уже сгруппированы в интервалы, 2)
- 7. Меры центральной тенденции Среднее арифметическое - частное от деления всех значений (Хi) на их количество (N)
- 8. Выбор меры центральной тенденции «Средняя температура по больнице?» Мода и медиана «не чувствительны» к выбросам (на
- 9. Меры изменчивости Размах (Р) – интервал между максимальным и минимальным значениями признака выборка: {1, 2, 3,
- 10. Меры изменчивости Среднее абсолютное отклонение (mad) – это среднеарифметическое разницы (по абсолютной величине) между каждым значением
- 11. Меры изменчивости Дисперсия (S²) — мера изменчивости, пропорциональная сумме квадратов отклонений значений от среднего S²= ,
- 12. Свойства дисперсии Если все значения равны друг другу, дисперсия равна 0 (нет рассеяния признака); Если ко
- 13. Меры изменчивости Стандартное отклонение (s) или (Sn) — мера изменчивости, являющаяся положительным значением квадратного корня из
- 14. Асимметрия и эксцесс Асимметрия и эксцесс характеризуют распределение признака в выборке, являются 3 и 4 моментами
- 15. Меры положения Квантиль — точка на числовой оси измеренного признака, которая делит всю совокупность измерений на
- 16. Какие описательные статистики можно применять… НА ШКАЛЕ НАИМЕНОВАНИЙ? НА РАНГОВОЙ ШКАЛЕ? НА ШКАЛЕ ИНТЕРВАЛОВ? НА ШКАЛЕ
- 18. Скачать презентацию















 совместно с Театром праздника «Солнечный зайчик»
совместно с Театром праздника «Солнечный зайчик» ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс
ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс Презентация на тему Врожденные и приобретенные программы поведения
Презентация на тему Врожденные и приобретенные программы поведения Презентация
Презентация ПРОЕКТНАЯ РАБОТА
ПРОЕКТНАЯ РАБОТА к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич
к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич Культура Руси в 10 – 13 веках
Культура Руси в 10 – 13 веках Болгария в 20-30-е годы
Болгария в 20-30-е годы Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя
Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя Приготовление завтрака
Приготовление завтрака «Инвестиционная политика муниципального образования на современном этапе»02.02.2012
«Инвестиционная политика муниципального образования на современном этапе»02.02.2012 Работа академии по направлению научно-технического творчества молодежи
Работа академии по направлению научно-технического творчества молодежи «Трудные» дети и их проблемы.
«Трудные» дети и их проблемы. Приемы расположения к себе. Самопрезентация
Приемы расположения к себе. Самопрезентация Автохимия. Завод автохимии
Автохимия. Завод автохимии Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года
Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года Евангелие от Матфея
Евангелие от Матфея Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов
Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов Аварийная аптечка для первой медицинской помощи
Аварийная аптечка для первой медицинской помощи Власть. Сила. Лекция 2
Власть. Сила. Лекция 2 Вітражі та шпроси
Вітражі та шпроси Моя будущая профессия - бухгалтер
Моя будущая профессия - бухгалтер Олимпиада үрләренә - баскычлап
Олимпиада үрләренә - баскычлап Общероссийские антидопинговые правила
Общероссийские антидопинговые правила Проектирование транспортно-грузовых комплексов
Проектирование транспортно-грузовых комплексов Определение размеров молекул октана
Определение размеров молекул октана Такси Лось
Такси Лось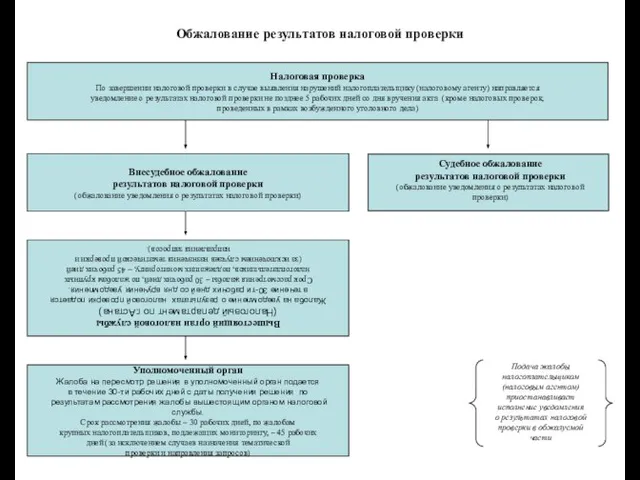 Обжалование результатов налоговой проверки
Обжалование результатов налоговой проверки