ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ

Внутренняя энергия. Работа и теплота
Наряду с механической энергией любое тело (или система) обладает внутренней энергией. Внутренняя энергия – энергия покоя. Она складывается из теплового хаотического движения молекул, составляющих тело, потенциальной энергии
их взаимного расположения, кинетической и потенциальной энергии электронов в атомах, нуклонов в ядрах и так далее.

В термодинамике важно знать не абсолютное значение внутренней энергии, а её изменение.
В термодинамических процессах изменяется только кинетическая энергия движущихся молекул. Следовательно, фактически под внутренней энергией в термодинамике подразумевают энергию теплового хаотического движения молекул.

Внутренняя энергия U одного моля идеального газа равна:
или
Таким образом, внутренняя энергия зависит только от температуры. Внутренняя энергия U является функцией состояния системы независимо от предыстории.
Внутренняя энергия идеального газа

В общем случае термодинамическая система может обладать как внутренней, так и механической энергией и разные системы могут обмениваться этими видами энергии.
Обмен механической энергией характеризуется совершенной работой А, а обмен внутренней энергией – количеством переданного тепла Q.

Количество теплоты, сообщаемой телу, идёт на увеличение внутренней энергии тела и на совершение телом работы:
– это и есть первое начало термодинамики или закон сохранения энергии в термодинамике.

В дифференциальном виде первое начало термодинамики будем иметь :
U – функция состояния системы; dU – её полный дифференциал, а δQ и δА таковыми не являются.

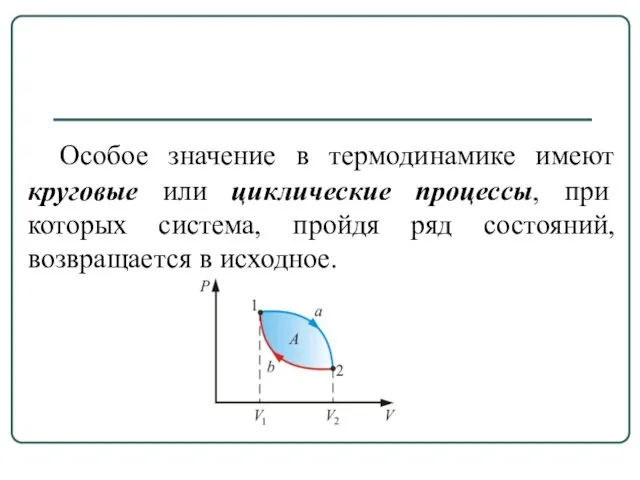
Особое значение в термодинамике имеют круговые или циклические процессы, при которых система, пройдя ряд состояний, возвращается в исходное.

Для цикла из первого начала термодинамики
Следовательно, нельзя построить периодически действующий двигатель, который совершал бы бóльшую работу, чем количество сообщенной ему извне энергии.
Одна из формулировок первого начала термодинамики: невозможно создать вечный двигатель первого рода.

Теплоёмкость идеального газа. Уравнение Майера
Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус
Удельная теплоёмкость (Суд) – есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус

Для газов удобно пользоваться молярной теплоемкостью Сμ − количество теплоты, необходимое для нагревания 1 моля газа на 1 градус.
Молярная масса – масса одного моля. Моль – количество вещества, в котором содержится
число молекул, равное числу атомов в 12 г изотопа
углерода 12С.

Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.
Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается СV.

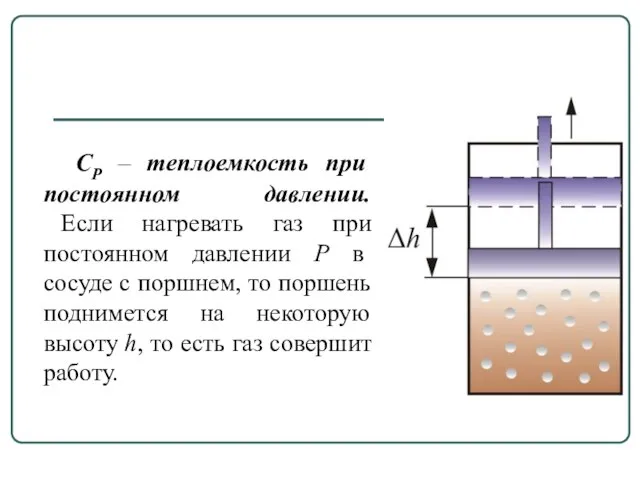
СР – теплоемкость при постоянном давлении.
Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу.

Следовательно, подводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что
Величины СР и СV оказываются связанными простым соотношением.

При нагревании одного моля идеального газа при постоянном объёме, первое начало термодинамики запишется в виде:
Теплоемкость при постоянном объёме будет равна:

В общем случае
так как U может зависеть не только от температуры. В случае идеального газа справедлива формула
Из этого следует, что

Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р), поэтому формула справедлива для любого процесса.
Для произвольной идеальной массы газа:

При изобарическом процессе кроме увеличения внутренней энергии происходит совершение работы газом:
Из уравнения Клапейрона-Менделеева
Подставив полученный результат в уравнение, получим

Это уравнение Майера для одного моля газа. Из него следует физический смысл универсальной газовой постоянной . R – численно равна работе, совершаемой одним молем газа при нагревании на один градус при изобарическом процессе.

Теплоёмкости одноатомных и многоатомных газов
Внутренняя энергия одного моля идеального газа равна

Теплоёмкости одноатомных газов
Теплоемкость при постоянном объеме СV – величина постоянная, от температуры не зависит.

Из уравнения Майера
Тогда, теплоемкость при постоянном давлении для одноатомных газов:

Полезно знать отношение:
где γ − коэффициент Пуассона

Так как
Тогда . Из этого следует, что
Кроме того где i – число степеней свободы молекул.

Подставив в выражение для внутренней энергии, получим:
а так как , то
внутреннюю энергию можно найти по формуле:

Необходимо учитывать вращательное и колебательное движение молекул. Число степеней свободы таких молекул
Молекулы многоатомных газов нельзя рассматривать как материальные точки.

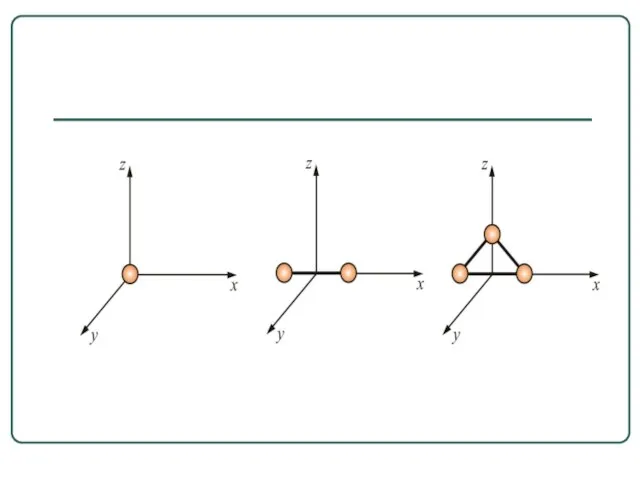
Числом степени свободы называется число независимых переменных, определяющих положение тела в пространстве и обозначается i
Как видно, положение материальной точки (одноатомной молекулы) задаётся тремя координатами, поэтому она имеет три степени свободы.

Многоатомная молекула может ещё и вращаться. Например, у двухатомных молекул вращательное движение можно разложить на два независимых вращения. Любое вращение можно разложить на три вращательных движения вокруг взаимно перпендикулярных осей. Но для двухатомных молекул вращение вокруг оси z не изменит её положение в пространстве.

У двухатомных жестких молекул пять степеней свободы (i = 5), а у трёхатомных шесть степеней свободы (i = 6).
Если молекула не жесткая, то она обладает еще колебательными степенями свободы. На каждую колебательную степень свободы приходится энергия, равная приходится на кинетическую энергию и на потенциальную .

Больцман доказал, что, средняя энергия, приходящаяся на одну степень свободы равна
Закон о равномерном распределении энергии по степеням свободы

На среднюю кинетическую энергию молекулы, имеющей i-степеней свободы приходится
Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы.

В общем случае, для молярной массы газа

Для произвольного количества газов:
,

Применение первого начала термодинамики к изопроцессам
Используем I начало термодинамики или закон сохранения энергии в термодинамике

Изотермический процесс
Изохорический процесс

Изобарический процесс
Адиабатный процесс

Рассмотрим политропный процесс – такой процесс, при котором изменяются все основные параметры системы, кроме теплоемкости, т.е. С = const.
Уравнение политропы
n – показатель политропы.

С помощью показателя n можно легко описать любой изопроцесс:
1. Изобарный процесс Р = const, n = 0
2. Изотермический процесс Т = const, n = 1,

Изохорный процесс
Адиабатический процесс ΔQ = 0, n = γ,
Сад = 0.

Во всех этих процессах работу можно вычислить по одной формуле: