Содержание
- 2. Повторение изученного № 549 C 20 15 A 30 B C1 A1 B1 Дано: ∆ABC ∾
- 3. ТЕОРЕМА: Первый признак подобия треугольников Если два угла одного треугольника соответственно равны двум углам другого, то
- 4. Дано: ∆ABC, ∆A1B1C1, ∠A=∠A1, ∠B=∠B1. Доказать: ∆ABC∾ ∆A1B1C1 Доказательство: 1.Так как по условию ∠A=∠A1, ∠B=∠B1, значит
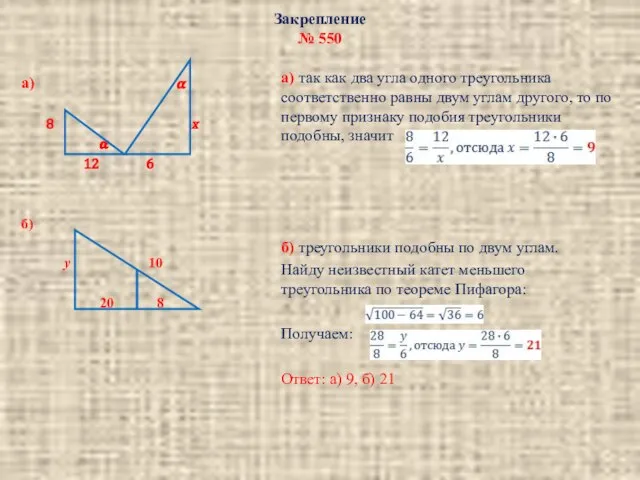
- 5. Закрепление № 550 а) ? 8 х ? 12 6 б) у 10 20 8 а)
- 6. Закрепление № 551а F C 4 E 8 D 7 10 B A Дано: ABCD –
- 7. Постановка домашнего задания Глава VII: §1, §2 (п59), вопросы 1-5, стр.160, теоремы с доказательствами, № 552
- 8. Взаимопроверка домашнего задания по образцу № 551 б F C E D B A Дано: ABCD
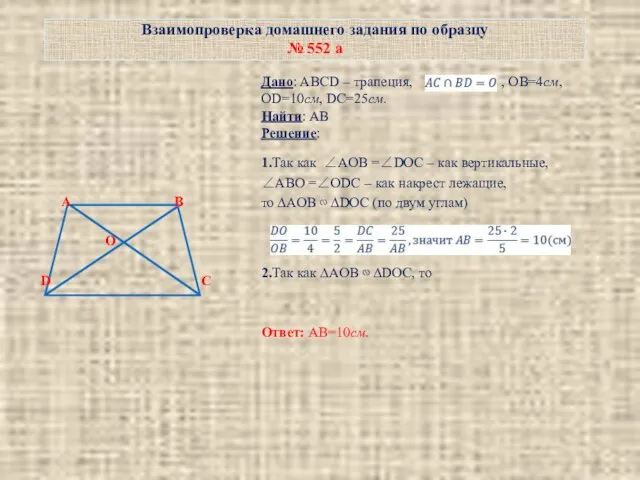
- 9. Взаимопроверка домашнего задания по образцу № 552 а A B O D C Дано: ABCD –
- 11. Скачать презентацию






 Отдельные виды договорных отношений в жилищном праве
Отдельные виды договорных отношений в жилищном праве Организация велостоянки для гимназии №1
Организация велостоянки для гимназии №1 О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го
О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го Урок русского языка в 6 классе по теме: «Правописание сложных существительных»
Урок русского языка в 6 классе по теме: «Правописание сложных существительных» Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании
Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании Невидимые нити в весеннем лесу (2 класс)
Невидимые нити в весеннем лесу (2 класс) Игрушки из носочков своими руками №7
Игрушки из носочков своими руками №7 Введение в специальность
Введение в специальность Герцог Ами
Герцог Ами Трение. Вредно или полезно
Трение. Вредно или полезно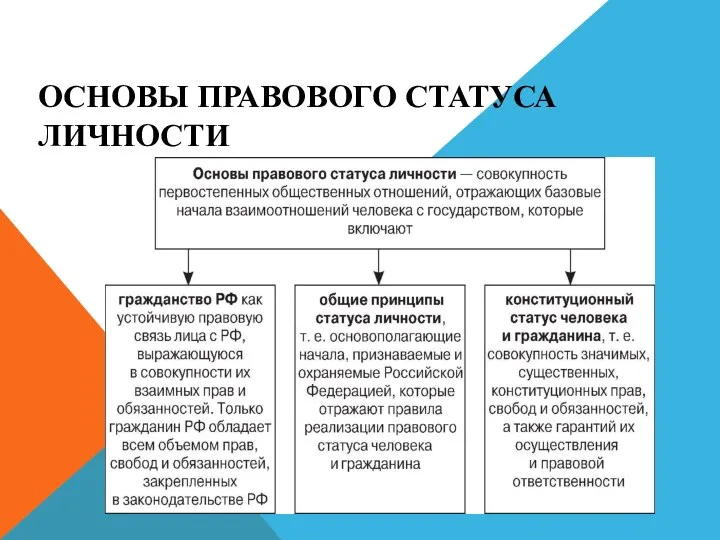 Правовой статус личности. Гражданство РФ
Правовой статус личности. Гражданство РФ Социальная психология
Социальная психология Презентация на тему АФАНАСИЙ НИКИТИН
Презентация на тему АФАНАСИЙ НИКИТИН  Теория обучения
Теория обучения Презентация на тему Our Environment (Наша окружающая среда)
Презентация на тему Our Environment (Наша окружающая среда) Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС)
Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС) Презентация по информатике на тему: «Устройства вывода информации, монитор.»
Презентация по информатике на тему: «Устройства вывода информации, монитор.» Круглопольское сельское поселение
Круглопольское сельское поселение Прайс косметологических услуг салона Забота о вас
Прайс косметологических услуг салона Забота о вас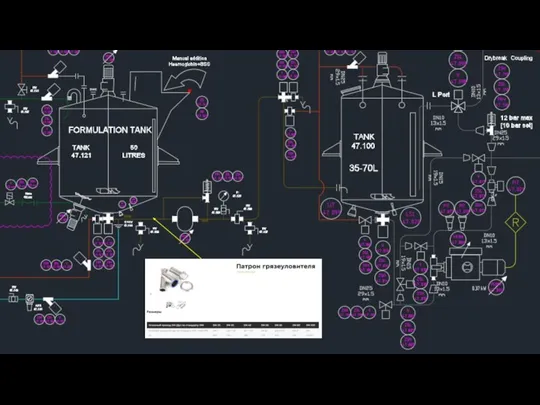 Патрон грязеуловителя
Патрон грязеуловителя Назначение изделия и его описание
Назначение изделия и его описание Планирование и организация процесса закупок материальных ресурсов промышленного предприятия
Планирование и организация процесса закупок материальных ресурсов промышленного предприятия Распространение объектно-ориентированного подхода на информационную безопасность
Распространение объектно-ориентированного подхода на информационную безопасность Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк.
Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк. Пейзаж в графике
Пейзаж в графике Рогожка. Коллекция однотонных штор
Рогожка. Коллекция однотонных штор _Презентация. Предоставление
_Презентация. Предоставление Презентация
Презентация