ПИФАГОР И ЕГО ТЕОРЕМА.

Пифагор родился в 570 году до н. э на острове Самос. Отцом Пифагора был Мнесарх – резчик по драгоценным камням. Имя матери Пифагора не сохранилось.
Многие считали, что Пифагор – это не имя, а прозвище. По многим античным свидетельствам, родившийся мальчик был удивительно красив, а вскоре проявил и свои незаурядные способности.
Среди учителей иного Пифагора были: старец Гермодамант и Ферекид Сиросский.
БИОГРАФИЯ

ЕГИПЕТ
В 550 году до н. э Пифагор принимает решение и отправляется в Египет. Итак, перед Пифагором открывается неизвестная страна и неведомая культура. Многое поражало и удивляло Пифагора в этой стране, и после некоторых наблюдений за жизнью египтян Пифагор понял, что путь к знаниям лежит через религию.
После одиннадцати лет
обучения в Египте, Пифагор
отправляется на Родину, где по
пути попадает в Вавилонский плен.

Вавилон
Здесь он знакомиться с вавилонской наукой, которая была более развита, чем Египетская. Вавилоняне умели решать линейные, квадратные и некоторые виды кубических уравнений. Они успешно применяли теорему Пифагора более чем за 1000 лет до Пифагора.

КРОТОН
В Кротоне начинается самый славный период в жизни Пифагора. Там он учредил нечто вроде религиозно-этического братства или тайного монашеского ордена, члены которого обязывались вести так называемый пифагорейский образ жизни.

Пифагор организовал религиозно-этическое братство, который впоследствии назовут пифагорейским союзом. Члены союза должны были придерживаться определённых принципов:
во-первых, стремиться к прекрасному и славному,
во-вторых, быть полезным,
в-третьих, стремиться к высокому наслаждению.
Пифагорейская школа

В школе Пифагора
Пифагорейская система занятий состояла из трёх разделов:
учения о числах – арифметике,
учения о фигурах – геометрии
учения о строении Вселенной – астрономии.
Музыка, гармония и числа были неразрывно связаны в учении Пифагорейцев. Математика и числовая мистика были фантастически перемешаны в нём.
В школе Пифагора открытия учеников приписывались учителю, поэтому практически не возможно было определить, что сделал Пифагор, а что его ученики.
Главным пифагорейским символом - символом здоровья и опознавательным знаком – была пентаграмма или пифагорейская звезда

В настоящее время все согласны с тем, что эта теорема не была открыта Пифагором. Она была известна еще задолго до него. Ее знали в Китае, Вавилонии, Египте. Вернее, не ее, а частные случаи. Однако полагают, что Пифагор первым дал ее полноценное доказательство.
Из истории теоремы

СОНЕТ
Легенда сообщает обстоятельства, сопровождавшие открытие теоремы.
Многим известен сонет Шамиссо:
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвопринашенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя ,вслед.
Они не в силах свету помешать ,
А могут лишь закрыв глаза дрожать
От страха, что вселил в них Пифагор.

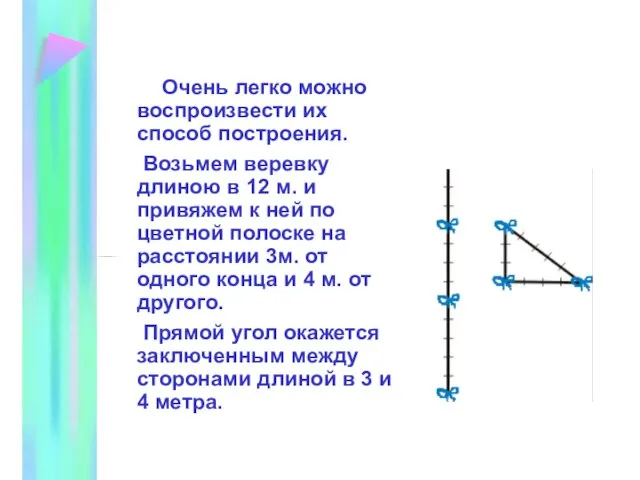
Очень легко можно воспроизвести их способ построения.
Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 м. от другого.
Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра.

ВАВИЛОН
Несколько больше было известно о теореме Пифагора вавилонянам. В одном тексте, относимом ко времени Хаммураби, т.е. к 2000 году до нашей эры, приводится приближенное вычисление гипотенузы прямоугольного треугольника; отсюда можно сделать вывод, что в
Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере, в некоторых случаях.

ИНДИЯ
Геометрия у индусов была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 8 века до нашей эры.
В сочинениях, относящихся к 4 или 5 веку до нашей эры, мы встречаемся с построением прямого угла при помощи треугольника
со сторонами 15, 36, 39.

Характерный чертеж теоремы Пифагора, который ныне иногда превращается школьниками, например, в облаченного в мантию профессора или человека в цилиндре, в те времена нередко употреблялся как символ математики.

Доказательство 1. (древнекитайское)‏
На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами a, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной a+b, а внутренний –
квадрат со стороной с,
построенный на гипотенузе.
(a + b)2 = 4ab/ 2 + c2
a2 + 2ab + b2 = 2ab + c2
или
a2 + b2 = c2
Доказательства ТЕОРЕМЫ ПИФАГОРА.

Доказательство 2. (Дж. Гардфилд 1882 г.)‏
Расположим два равных прямоугольных треугольника так, чтобы катет одного из них был продолжением другого
Площадь рассматриваемой трапеции находится как произведение полусуммы оснований на высоту
S = (a + b)·(a + b)
2
C другой стороны, площадь трапеции равна сумме площадей полученных треугольников: S = 2ab + c2
2 2
Приравнивая данные выражения, получаем:
a2 + b2 = c2

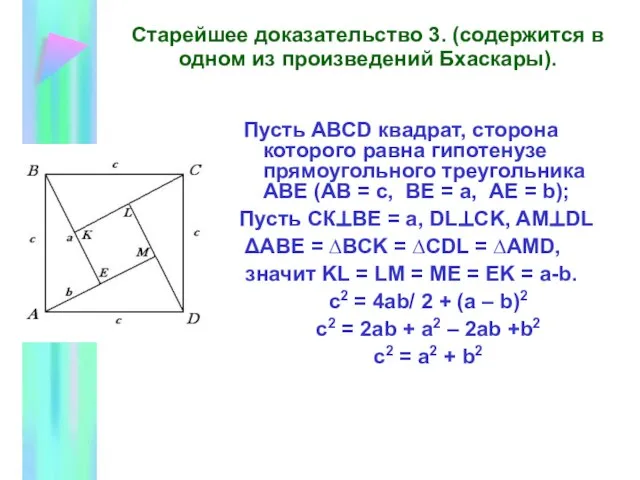
Старейшее доказательство 3. (содержится в одном из произведений Бхаскары).
Пусть АВСD квадрат, сторона которого равна гипотенузе прямоугольного треугольника АВЕ (АВ = с, ВЕ = а, АЕ = b);
Пусть СК⊥ВЕ = а, DL⊥CK, AM⊥DL
ΔABE = ∆BCK = ∆CDL = ∆AMD,
значит KL = LM = ME = EK = a-b.
c2 = 4ab/ 2 + (a – b)2
c2 = 2ab + a2 – 2ab +b2
c2 = a2 + b2

Доказательство 4 (простейшее)‏
Это доказательство получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников чтобы убедиться в справедливости теоремы. Например, для треугольника АВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, - по два.

Доказательство 5.
Квадрат со стороной (a+b), можно разбить на части либо как на рисунке а), либо как на рисунке b). Ясно, что треугольники на обоих рисунках одинаковы. А если от равных (площадей) отнять равные, то и останутся равные.
Впрочем, древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали лишь одним словом: Смотри!

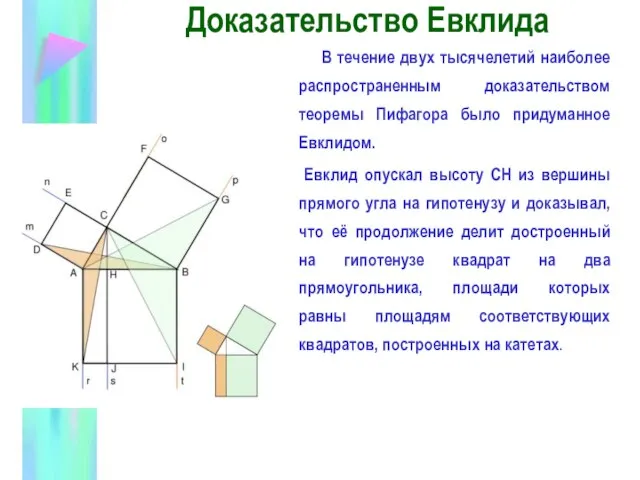
Доказательство Евклида
В течение двух тысячелетий наиболее распространенным доказательством теоремы Пифагора было придуманное Евклидом.
Евклид опускал высоту СН из вершины прямого угла на гипотенузу и доказывал, что её продолжение делит достроенный на гипотенузе квадрат на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах.

1. Задача индийского математика XII века Бхаскары
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Задачи:

2. Периметр ромба 68 см., а одна из его диагоналей равна 30 см. Найдите длину другой диагонали ромба.
3. На сторонах прямоугольного треугольника построены квадраты, причем
S1-S2=112 см2, а S3=400 см2. Найдите периметр треугольника.
4. Дан треугольник АВС, угол С=90°, CD перпендикулярна AB, AC=15 см., AD=9 см. Найдите АВ.
Задачи:

5. Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?
Задачи:

6. Задача из учебника "Арифметика" Леонтия Магницкого
"Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп.
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."

7. Задача из китайской "Математики в девяти книгах"
"Имеется водоем со стороной в 1 чжан = 10 чи.
В центре его растет камыш, который выступает над водой на 1 чи.
Если потянуть камыш к берегу, то он как раз коснётся его.
Спрашивается: какова глубина воды и какова длина камыша?"

Заключение
Мы изучили ряд исторических и математических источников, в том числе информацию в Интернете, и увидели, что теорема Пифагора интересна не только своей историей, но и тем, что она занимает важное место в жизни и науке. Об этом свидетельствуют приведённые нами в данной работе различные трактовки текста этой теоремы и пути её доказательства.
Заслуга же Пифагора состояла в том, что он дал полноценное научное доказательство этой теоремы.
Интересна личность самого учёного, память о котором неслучайно сохранила эта теорема. Пифагор – замечательный оратор, учитель и воспитатель, организатор своей школы, ориентированной на гармонию музыки и чисел, добра и справедливости, на знания и здоровый образ жизни. Он вполне может служить примером для нас, далёких потомков.