пирамида

Определение
Многогранник, составленный из многоугольника A1A2…An и n треугольников называется n-угольной пирамидой

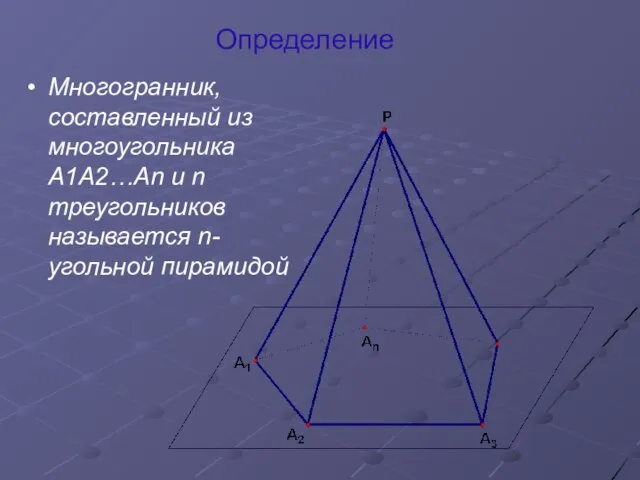
Многоугольник A1A2…An называется основанием пирамиды,
треугольники A1PA2 , A2PA3 , … , AnPA1 – боковыми гранями пирамиды.
Точка P называется вершиной пирамиды, а отрезки PA1, PA2, …,PAn - её боковыми ребрами.

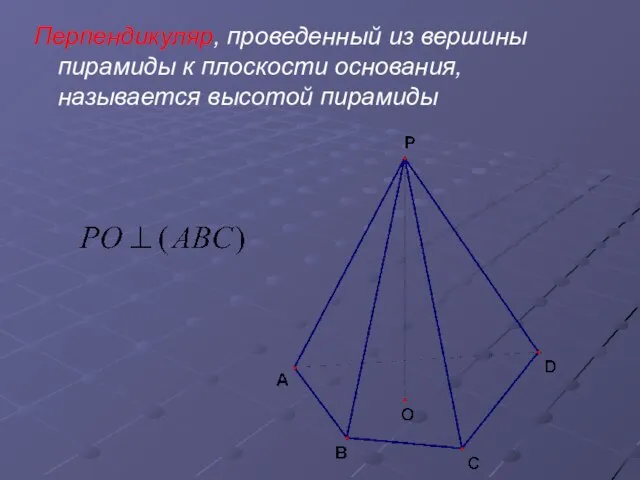
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды

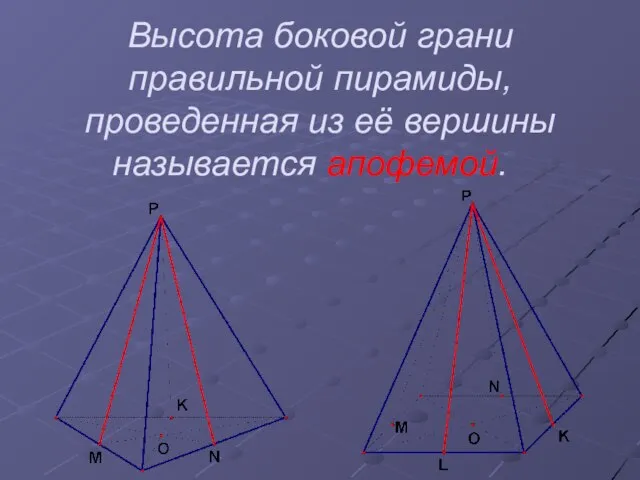
Высота боковой грани правильной пирамиды, проведенная из её вершины называется апофемой.

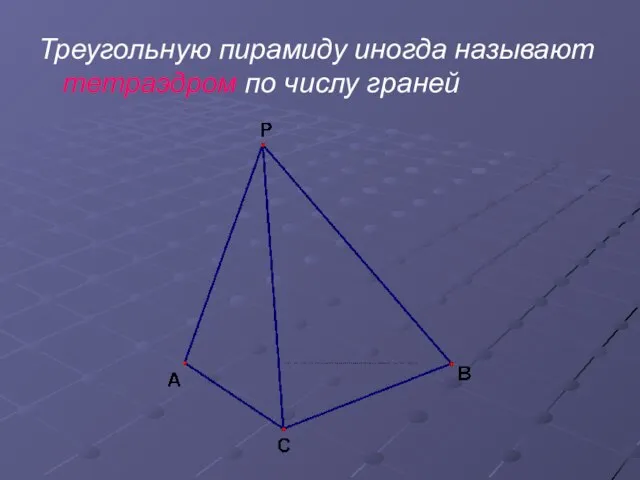
Треугольную пирамиду иногда называют тетраэдром по числу граней

Правильные пирамиды

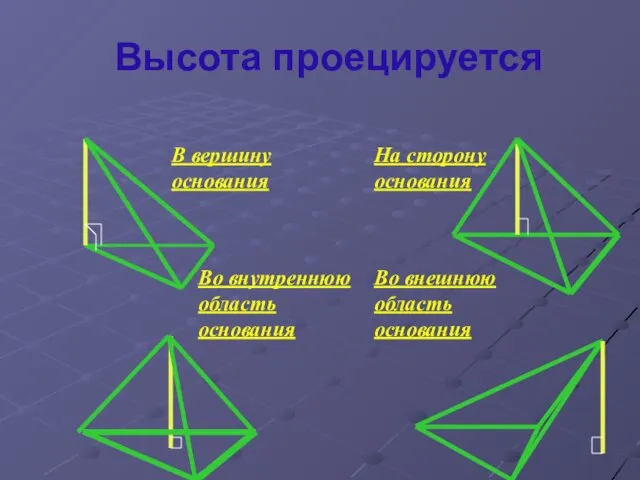
Высота проецируется
В вершину основания
На сторону основания
Во внутреннюю область основания
Во внешнюю область основания

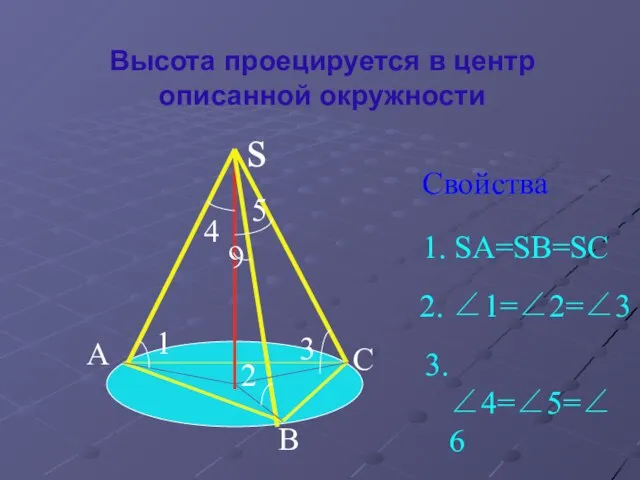
Высота проецируется в центр описанной окружности
Свойства
s
A
B
C
1
2
3
6
4
5
1. SA=SB=SC
2. ∠1=∠2=∠3
3. ∠4=∠5=∠6

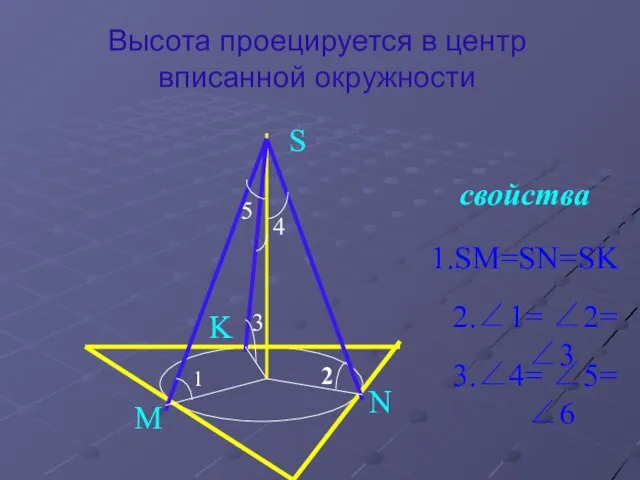
Высота проецируется в центр вписанной окружности
свойства
S
M
N
K
1
2
3
4
5
1.SM=SN=SK
2.∠1= ∠2= ∠3
3.∠4= ∠5= ∠6

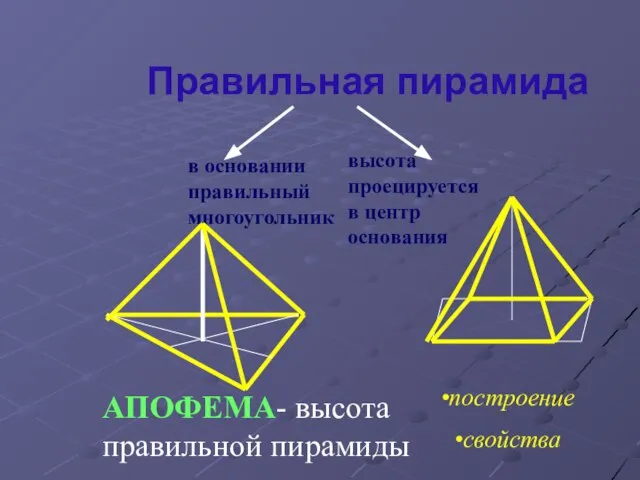
Правильная пирамида
в основании правильный многоугольник
высота проецируется в центр основания
построение
свойства
АПОФЕМА- высота правильной пирамиды

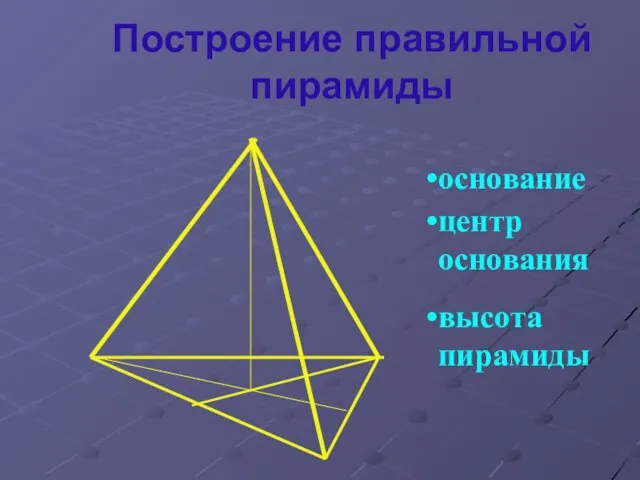
Построение правильной пирамиды
высота пирамиды
основание
центр основания

Свойства правильной пирамиды
SA=SB=SC
Боковые ребра образуют равные углы с плоскостью основания
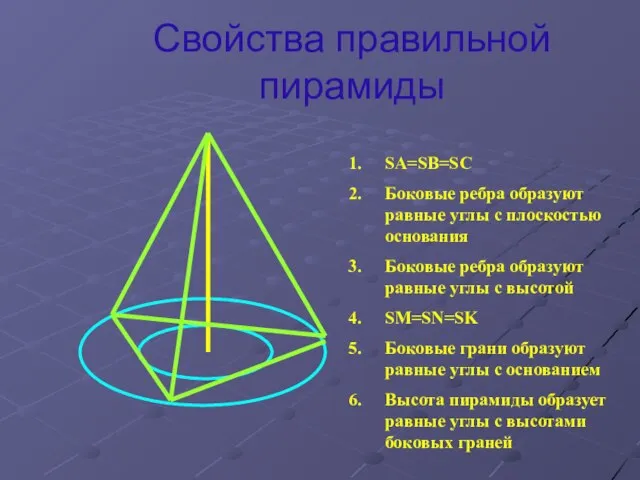
Боковые ребра образуют равные углы с высотой
SM=SN=SK
Боковые грани образуют равные углы с основанием
Высота пирамиды образует равные углы с высотами боковых граней