Плотность распределения

?
f (x) − дифференциальная ФР

Свойства плотности распределения
Следуют из определения ПР
Точное равенство при Δx = dx
P { X∈ ( x, x+dx )}
= f ( x )⋅dx = dP
dP − элемент вероятности

«Если Δx = 0, то Р = 0» →
«вероятность попадания X в (⋅)
равна 0» (это невозможное событие)
Попадание непрерывной CВ в (⋅)
лишено физического смысла →
говорят о «попадании в бесконечно малый интервал
в окрестности (⋅) х »
Аналогия с механикой:
dm = ρ(x) ⋅ dx
F(x) − интегральная ФР

to be continued
Соответствует свойству (г) ФР.
Важно для практики!
Вероятность попадания СВ в любой интервал ее значений можно определить, если известны ФР или ПР

=?
= 1
Эти выражения еще раз утверждают:
сумма вероятностей всех возможных значений СВ равна
единице
(вероятности достоверного события − неизбежно принять одно из значений)
Бесконечная сумма dP
во всем диапазоне значений X
или в более общей форме
= 1
=?

График функции плотности −
к р и в а я р а с п р е д е л е н и я
Три примера «3 пары графиков ФР и кривых распределения» → иллюстрируют суть, взаимосвязь свойств и практическую пользу
ФР и ПР

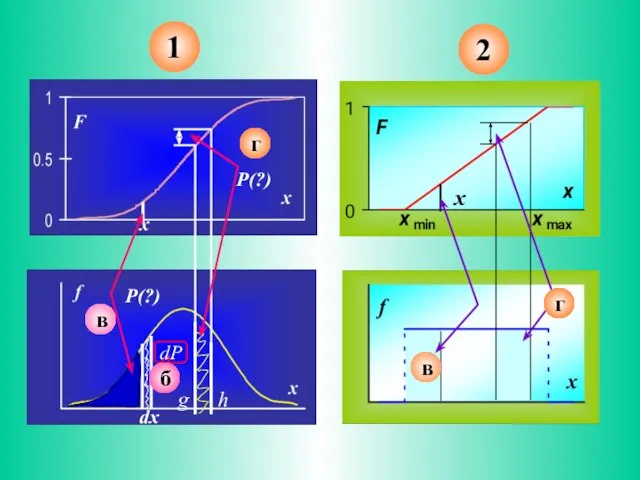
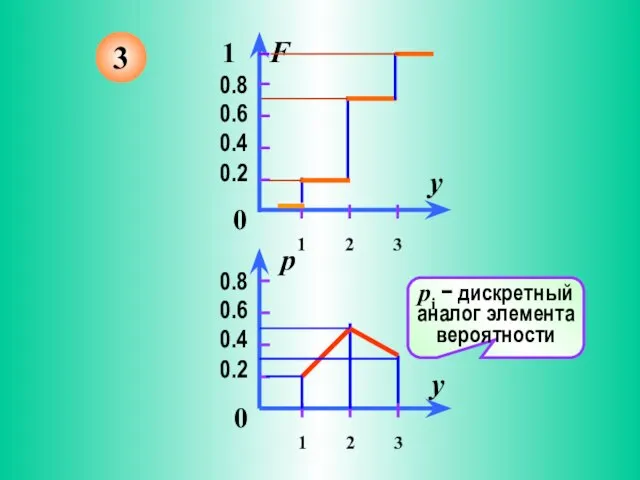
Графическая интерпретация свойств функции и плотности распределения
2 пары графиков описывают непрерывные СВ
3-я пара представляет ЗР дискретной величины
На всех верхних − ФР,
на нижних показаны функции «плотности»:
кривые распределения − графики производных (1, 2)
и ломаная линия полигона распределения (3)
Полигон − дискретный аналог кривой распределения:
вероятности сконцентри-рованы в нескольких отдельных точках
шансы распределены между бесчисленным числом точек

б

3
pi − дискретный аналог элемента вероятности

Графические образы явно демонстрируют свойство (а)
Вероятность того, что X примет значение между g и h равна:
1) разности ординат F для g и h или
2) площади под кривой распределения между g и h
Площадь под всей кривой распределения равна единице
Площадь под любой кривой распределения равна единице

Различия между разными ЗР заключается в том, как единичная площадь распределена
вдоль (между участками) числовой оси
Значения разных величин распределены вдоль числовой оси в соответствии с разной мерой возможности → вероятностной мерой f ( x )