Содержание
- 2. плотность распределения ( ПР ) или функция плотности или плотность вероятности дифференциальная ФР интегральная ФР вероятностная
- 3. Функция распределения − наиболее общая, универсальная форма описания СВ − и дискретных, и непрерывных Функция распределения
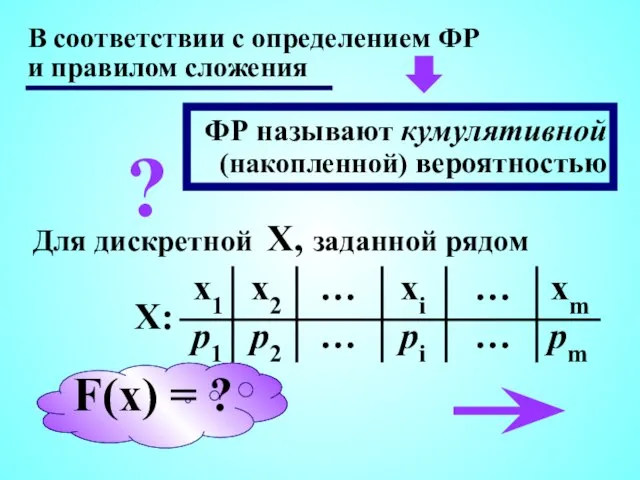
- 4. В соответствии с определением ФР и правилом сложения ФР называют кумулятивной (накопленной) вероятностью Для дискретной X,
- 5. Для x в разных диапазонах значений: 0 , x ≤ x1 p1, x1 p1 + p2,
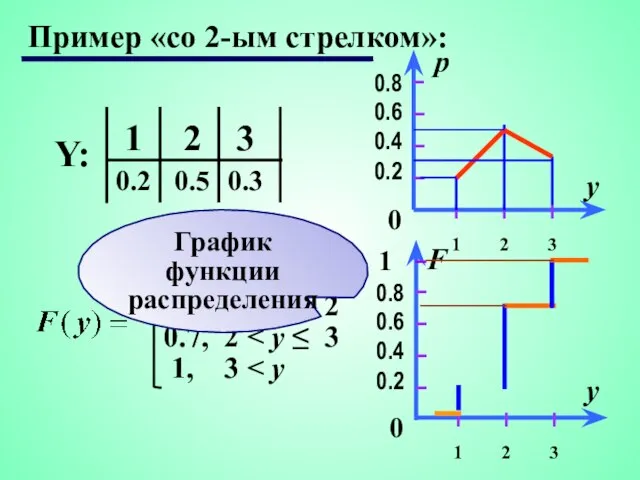
- 6. Пример «со 2-ым стрелком»: 0, y ≤ 1 0.2, 1 0.7, 2 1, 3 График функции
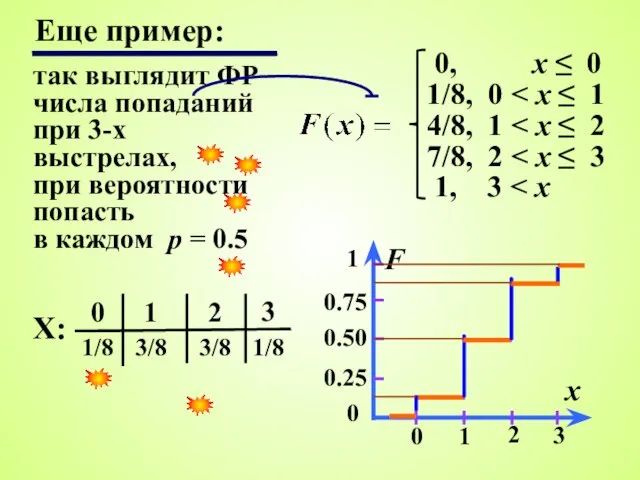
- 7. Еще пример: так выглядит ФР числа попаданий при 3-х выстрелах, при вероятности попасть в каждом p
- 8. Ее скачки соответствуют возможным значениям величины и равны вероятностям этих значений. ФР дискретной СВ − это
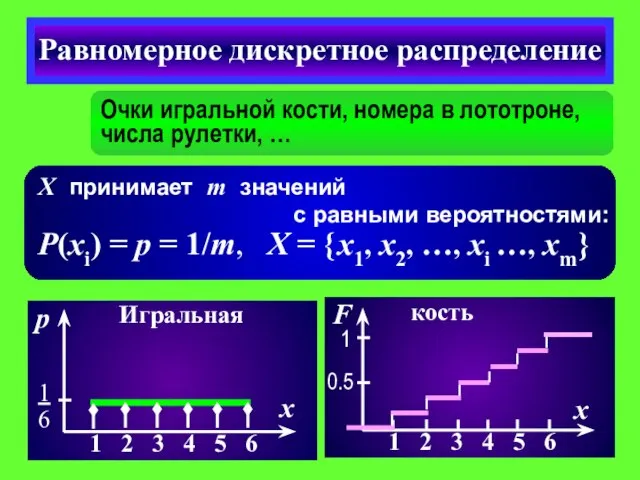
- 9. Очки игральной кости, номера в лототроне, числа рулетки, … Равномерное дискретное распределение X принимает m значений
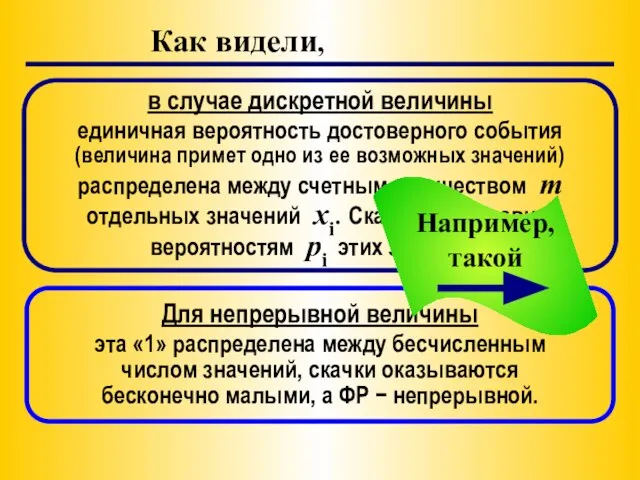
- 10. Как видели, в случае дискретной величины единичная вероятность достоверного события (величина примет одно из ее возможных
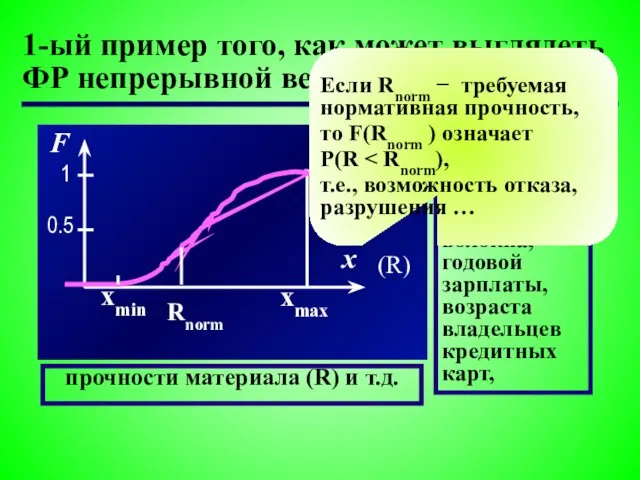
- 11. 1-ый пример того, как может выглядеть ФР непрерывной величины прочности материала (R) и т.д. Это может
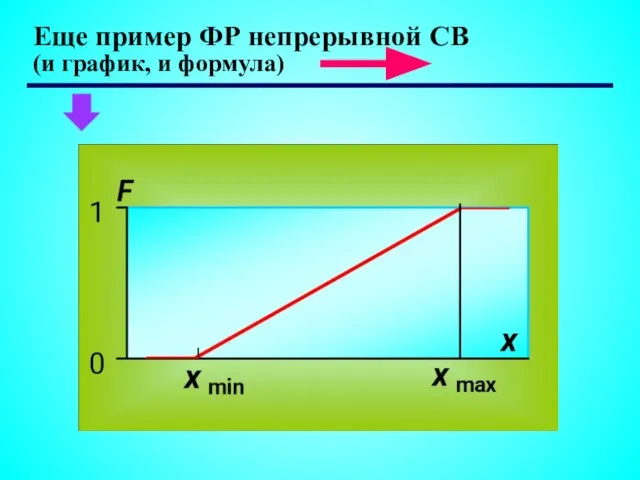
- 12. Еще пример ФР непрерывной СВ (и график, и формула)
- 13. F(X) растет с ростом x обратно пропорционально диапазону значений Равномерный закон распределения Например: так распределено время
- 14. Свойства функции распределения Следуют из определения ФР to be continued
- 15. Следует из правила сложения вероятностей: пусть А ~ {Х тогда B = A + C, P(B)
- 16. Пример: Поезд в метро приходит с интервалом в 4 мин. Учитывая, что время ожидания τ распределено
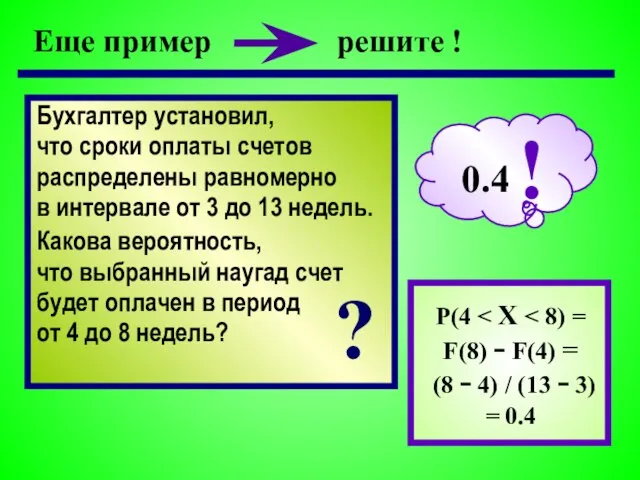
- 17. Еще пример P(4 (8 − 4) / (13 − 3) = 0.4 Бухгалтер установил, что сроки
- 18. Плотность распределения Если ФР непрерывна и дифференцируема, то существует другая удобная форма полного описания непрерывной СВ.
- 20. Скачать презентацию









 Порядок регистрации и получения патента на изобретение
Порядок регистрации и получения патента на изобретение Жизненный цикл человеческого капитала. Тема 3
Жизненный цикл человеческого капитала. Тема 3 Старинные меню
Старинные меню Менеджмент и предпринимательство в дизайне
Менеджмент и предпринимательство в дизайне фразеологизмы
фразеологизмы RISC-архитектуры(Reduced Instruction Set Computer)
RISC-архитектуры(Reduced Instruction Set Computer) Схемы учебно-тренировочного комплекса 211, отдельного железнодорожного батальона механизации
Схемы учебно-тренировочного комплекса 211, отдельного железнодорожного батальона механизации Фёдорова Наталья Петровна
Фёдорова Наталья Петровна Китай
Китай ГИПЕРМАРКЕТ________ В ВАШЕМ ГОРОДЕ
ГИПЕРМАРКЕТ________ В ВАШЕМ ГОРОДЕ Презентация на тему Реформы Петра в области образования
Презентация на тему Реформы Петра в области образования  Золотой век алхимии
Золотой век алхимии Педагогический совет
Педагогический совет 1 сентября - День знаний
1 сентября - День знаний Яндекс. Постконтекстная реклама
Яндекс. Постконтекстная реклама Презентация на тему Строение, свойства костей. Типы их соединения
Презентация на тему Строение, свойства костей. Типы их соединения Interesting holiday in Australia
Interesting holiday in Australia Правовые акты управления
Правовые акты управления Экологические проблемы Байкала
Экологические проблемы Байкала Колледж ландшафтного дизайна №18
Колледж ландшафтного дизайна №18 Связь справедливости взаимодействия с эмоциями участников (на примере политических выборов)
Связь справедливости взаимодействия с эмоциями участников (на примере политических выборов) My mind about School
My mind about School Получение атомарно-чистой поверхности германия методом ионного травления
Получение атомарно-чистой поверхности германия методом ионного травления Распознавание слов по вопросам, точное употребление слов в предложении
Распознавание слов по вопросам, точное употребление слов в предложении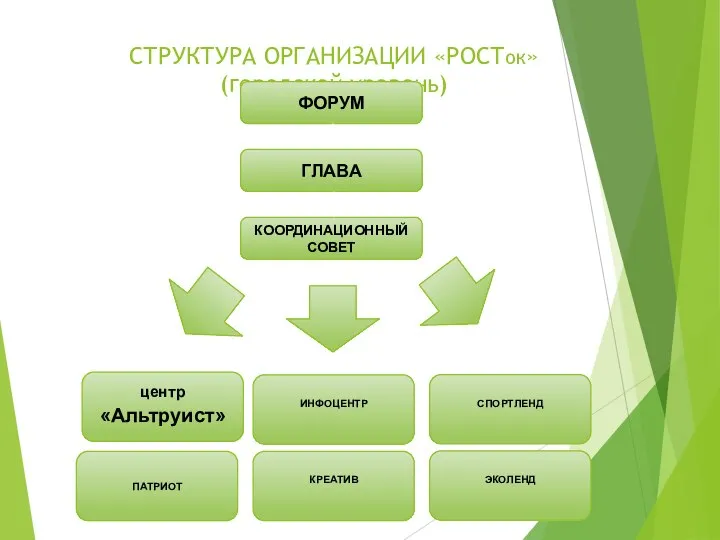 Структура организации РОСТок
Структура организации РОСТок Презентация на тему Язык разметки гипертекста HTML
Презентация на тему Язык разметки гипертекста HTML Поделки из ракушек, морских камней и шишек
Поделки из ракушек, морских камней и шишек Нестандартные способы продвижения интернет-сайта
Нестандартные способы продвижения интернет-сайта