Содержание
- 2. Тема 6: Показатели в форме средних величины План Понятие средней величины Виды средних величин Особенности и
- 3. Какая бригада работает оперативнее? Бригада А, в минутах: 10; 19; 15; 20; 13; 40; 11; 18;
- 4. Какая бригада работает оперативнее? Бригада А Среднее время в минутах: 202 : 10 = 20,2 мин.
- 5. Средняя величина – обобщающая количественная характеристика признака на единицу конкретной совокупности или группы
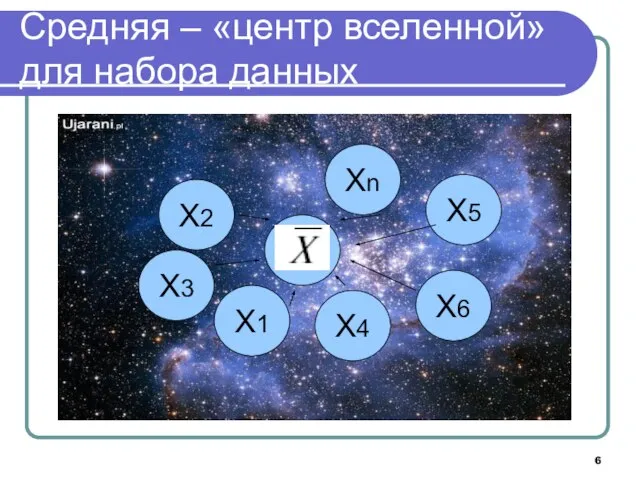
- 6. Средняя – «центр вселенной» для набора данных Х3 Х2 Хn Х5 Х6 Х1 Х4 Х1
- 7. Нужны ли нам средние??? X __
- 8. Определяющее свойство средней величины Определяющее свойство средней величины X1 = 200 X2 = 300 X3 =
- 9. Объективность средней Средняя дает наиболее объективный результат только при качественной однородности объектов доход 6 000 руб.
- 10. Объективность средней доход 8 000 руб. 10 000 руб. 6 000 руб. = 8 000 руб.
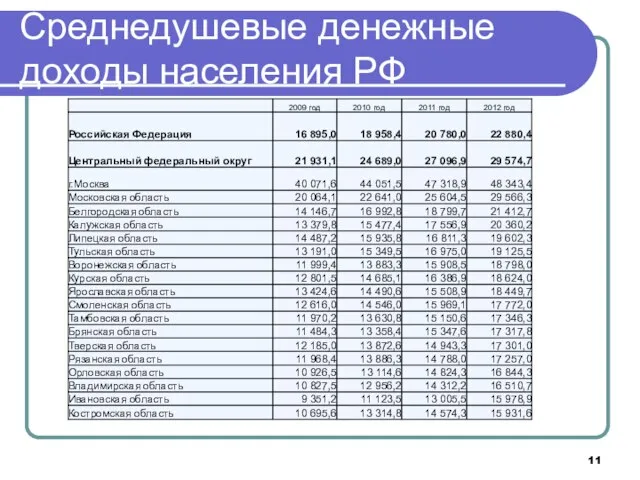
- 11. Среднедушевые денежные доходы населения РФ
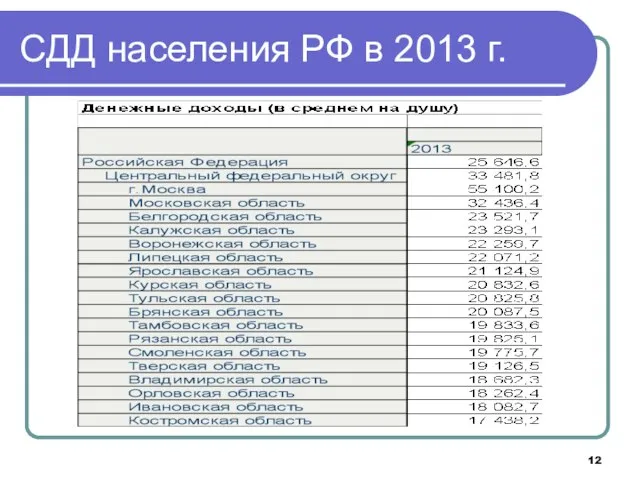
- 12. СДД населения РФ в 2013 г.
- 13. Кто на каком месте по уровню дохода за 2012 и 2013 гг? ?
- 14. Доходы глав государств за 2012 и 2013 гг. 290 тыс. евро 380-590 тыс.евро 530 тыс. евро
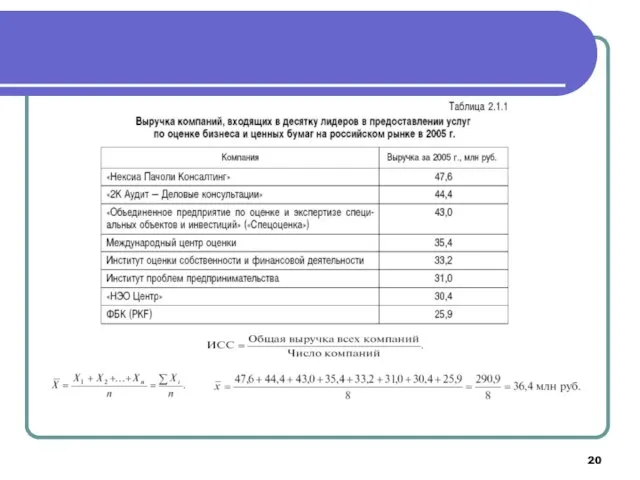
- 15. Логическая формула средней Общая логическая формула средней - ИСС – исходное соотношение средней Для каждого вида
- 16. Примеры ИСС Средний стаж работы судьи = Средний возраст совершения преступления несовершеннолетними = Средний счет в
- 17. Примеры ИСС Средний размер одного вклада в банк
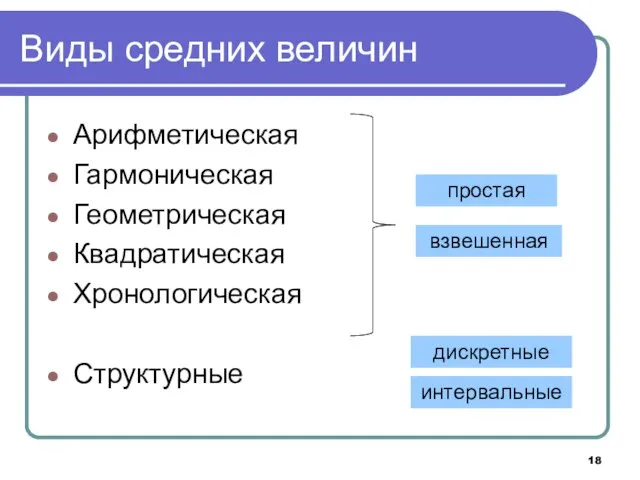
- 18. Виды средних величин Арифметическая Гармоническая Геометрическая Квадратическая Хронологическая Структурные взвешенная простая дискретные интервальные
- 19. Средняя арифметическая Простая – используется для расчета средней по несгруппированным данным или по группировкам с равными
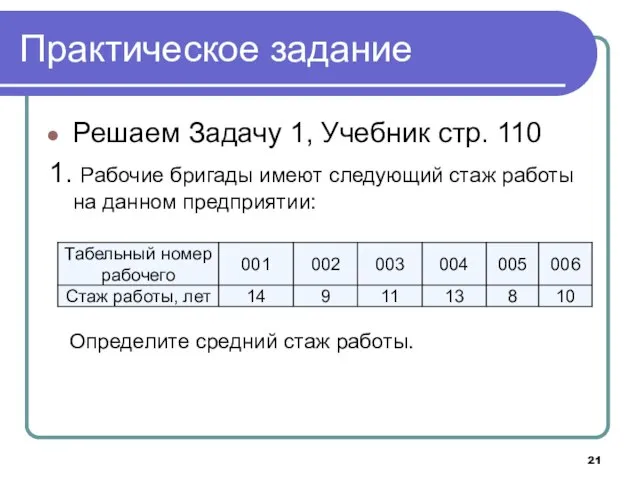
- 21. Решаем Задачу 1, Учебник стр. 110 1. Рабочие бригады имеют следующий стаж работы на данном предприятии:
- 22. Средняя арифметическая Взвешенная – используется для расчета средней по группировкам и рядам распределения Xi – значение
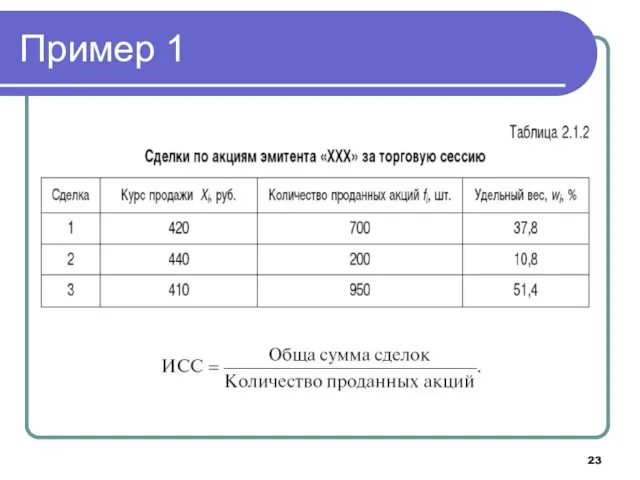
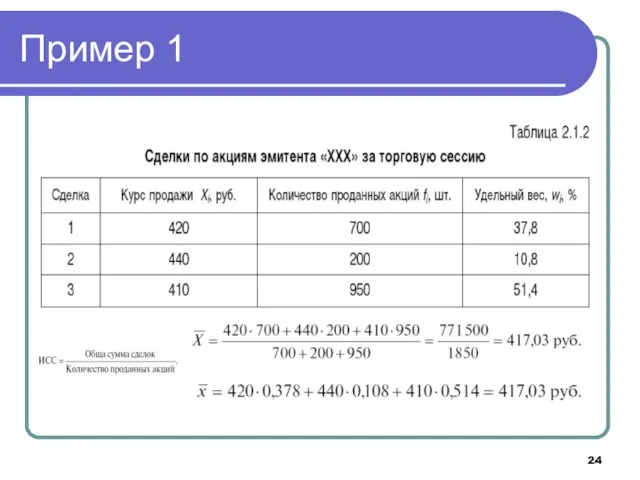
- 23. Пример 1
- 24. Пример 1
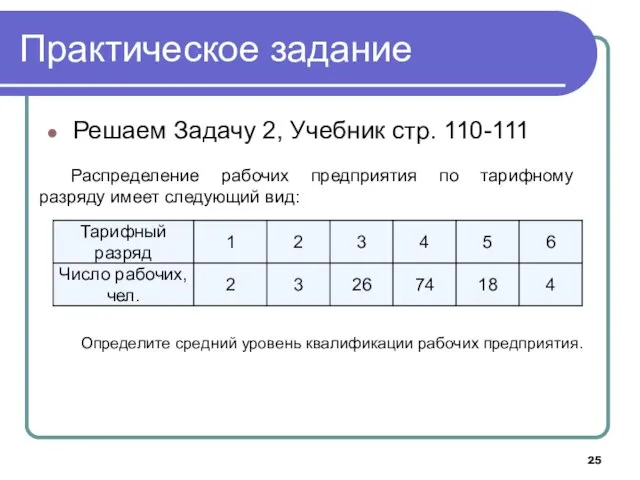
- 25. Практическое задание Решаем Задачу 2, Учебник стр. 110-111 Распределение рабочих предприятия по тарифному разряду имеет следующий
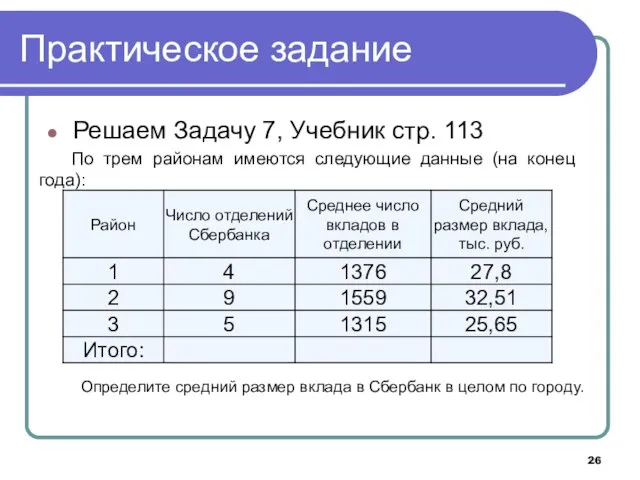
- 26. Практическое задание Решаем Задачу 7, Учебник стр. 113 По трем районам имеются следующие данные (на конец
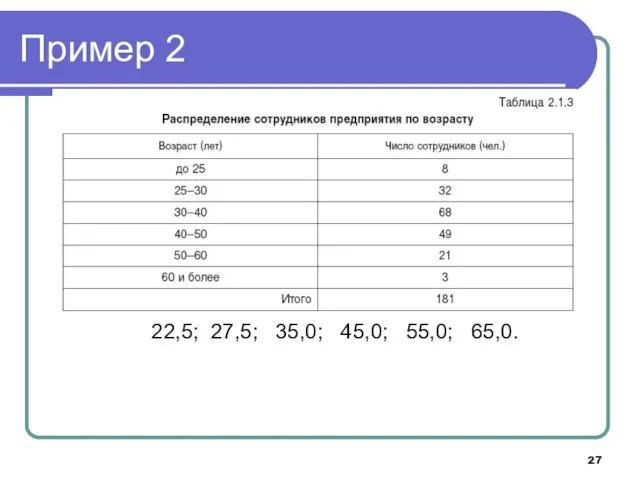
- 27. Пример 2 22,5; 27,5; 35,0; 45,0; 55,0; 65,0.
- 28. Определение середины открытого интервала Ширина открытого интервала условно приравнивается к ширине соседнего закрытого интервала. Зная ширину,
- 29. Пример 2 22,5; 27,5; 35,0; 45,0; 55,0; 65,0.
- 30. Пример 3
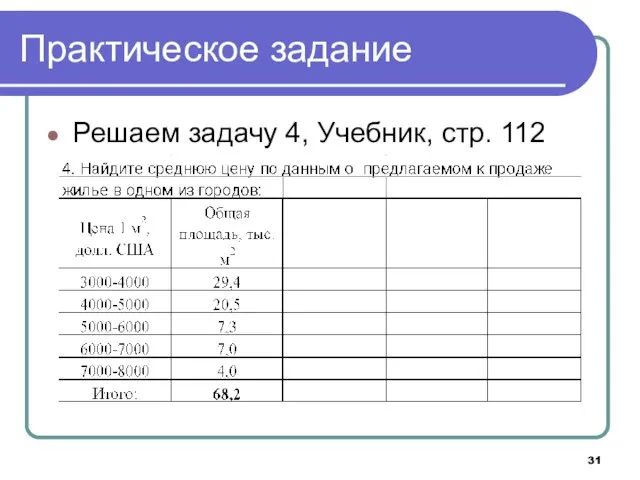
- 31. Практическое задание Решаем задачу 4, Учебник, стр. 112
- 32. Практическое задание Решаем задачу 5, Учебник, стр. 112 Найдите среднедушевые денежные доходы по следующим данным
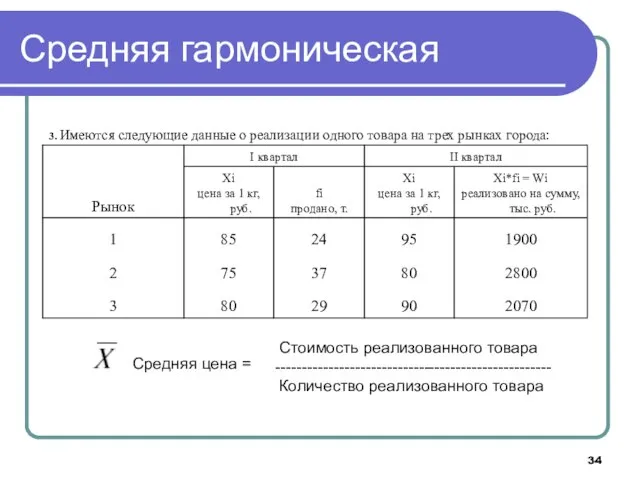
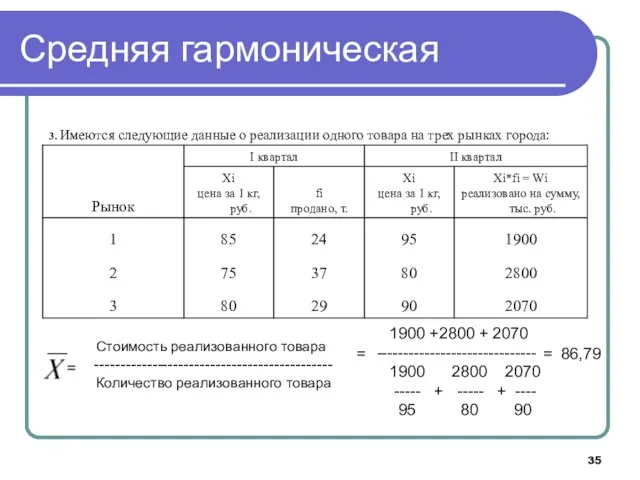
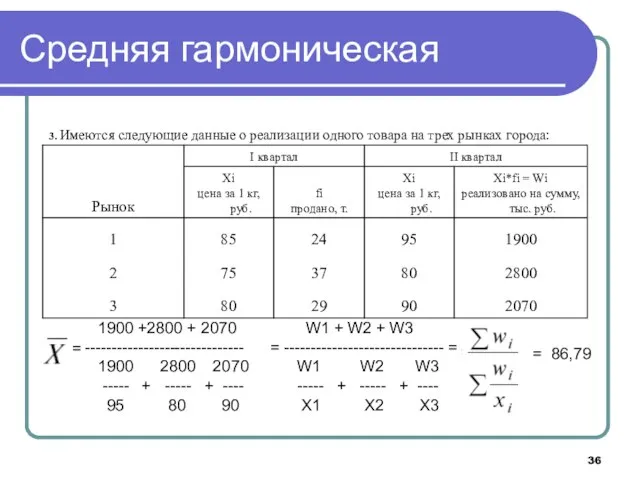
- 33. Средняя гармоническая Средняя гармоническая используется в случаях, когда в исходных данных нет прямой информации о количестве
- 34. Средняя гармоническая Средняя цена = Стоимость реализованного товара ---------------------------------------------------- Количество реализованного товара
- 35. Средняя гармоническая = = 1900 +2800 + 2070 ------------------------------ 1900 2800 2070 ----- + ----- +
- 36. Средняя гармоническая W1 + W2 + W3 = ------------------------------ = W1 W2 W3 ----- + -----
- 37. Средняя гармоническая взвешенная Средняя гармоническая чаще используется во взвешенной форме = Xi*fi = Wi
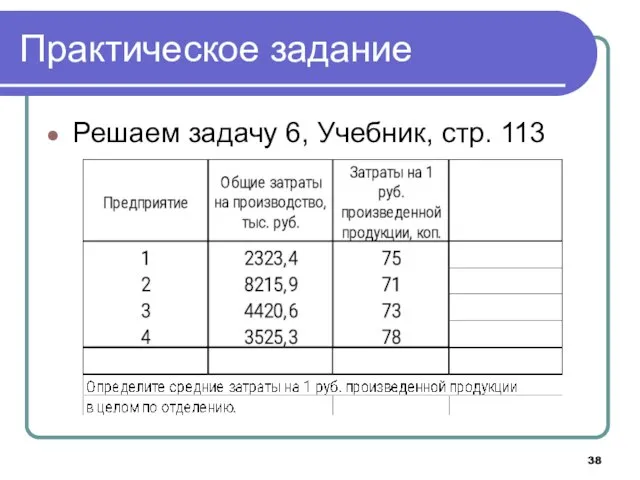
- 38. Практическое задание Решаем задачу 6, Учебник, стр. 113
- 39. Средняя геометрическая Используется в основном для расчета средних аналитических показателей в рядах динамики.
- 40. Средняя квадратическая Средняя квадратическая рассчитывается по формулам Невзвешенная Взвешенная
- 41. Структурные средние Мода (Мo) представляет собой значение признака, повторяющееся с наибольшей частотой. Медианой (Мe) называется значение
- 42. Методики расчета Мо и Ме для дискретных и интервальных рядов РАЗЛИЧАЮТСЯ !!!
- 43. Мо и Ме в дискретном ряду Оптовые цены товара «XXX», тыс. рублей 4,4 4,3 4,4 4,5
- 44. Мо и Ме в дискретном ряду Доходы потребителей полиграфического издания Ме = NМе = (100+1)/2 =
- 45. Мо и Ме в дискретном ряду Ме = ?
- 46. Мо и Ме в дискретном ряду Ме = 54 По накопленным частотам видно, что цена «52»
- 47. Практическое задание Решаем задачу 10, Учебник, стр. 115
- 48. Материалы слайдов 49-59 будут рассмотрены на лекции №5.
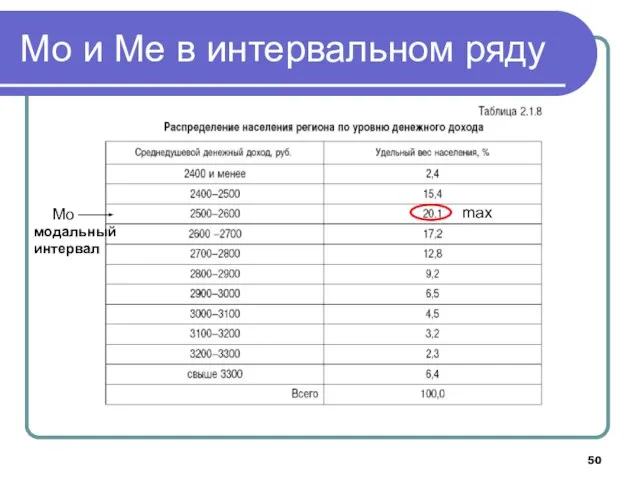
- 49. Мо и Ме в интервальном ряду
- 50. max Mo модальный интервал Мо и Ме в интервальном ряду
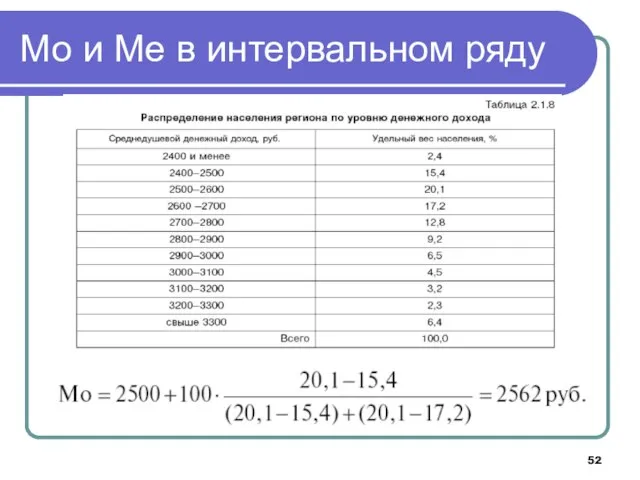
- 51. Мо и Ме в интервальном ряду
- 52. Мо и Ме в интервальном ряду
- 53. Мо и Ме в интервальном ряду
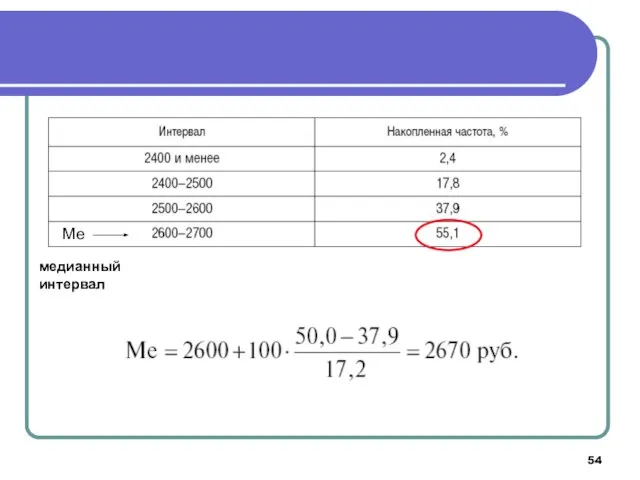
- 54. Ме медианный интервал
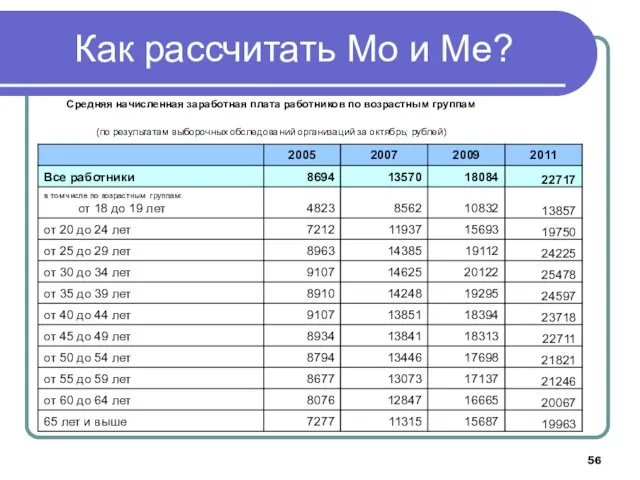
- 56. Как рассчитать Мо и Ме?
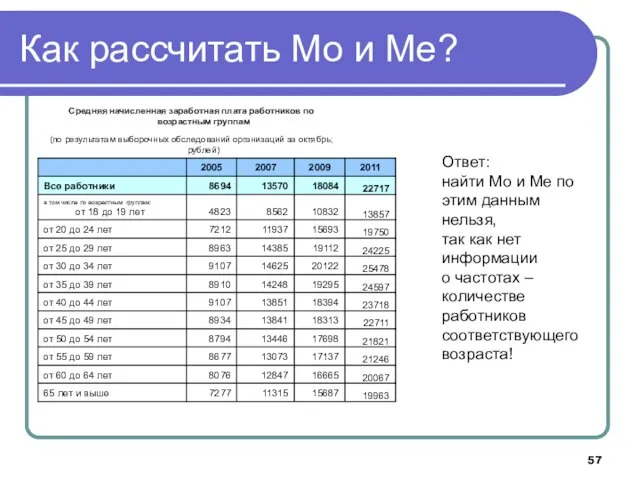
- 57. Как рассчитать Мо и Ме? Ответ: найти Мо и Ме по этим данным нельзя, так как
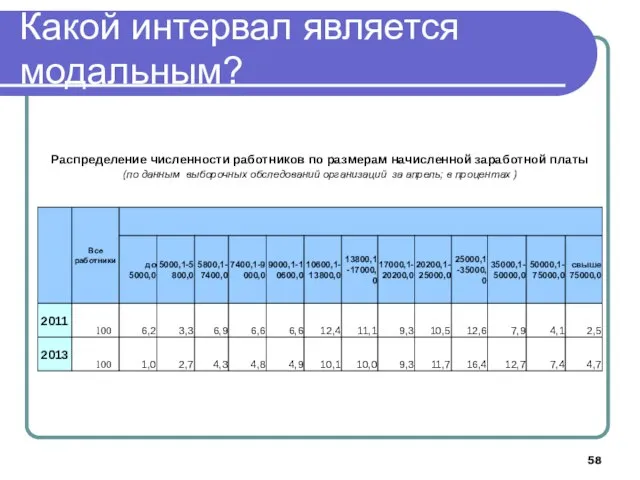
- 58. Какой интервал является модальным?
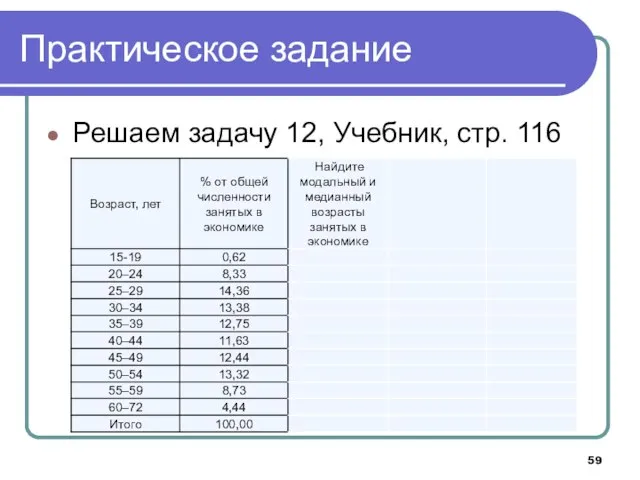
- 59. Практическое задание Решаем задачу 12, Учебник, стр. 116
- 61. Скачать презентацию


































 Мезозойская эра в эволюции
Мезозойская эра в эволюции Конструктор цветной прозрачный блок 1
Конструктор цветной прозрачный блок 1 Мудрость родительской любви
Мудрость родительской любви Презентация на тему Склонение имён существительных
Презентация на тему Склонение имён существительных Природные явления
Природные явления ГТО – это спорт, а спорт это жизнь! 3 класс
ГТО – это спорт, а спорт это жизнь! 3 класс Презентация на тему Объёмы геометрических тел
Презентация на тему Объёмы геометрических тел  Задачи по геометрии
Задачи по геометрии Болезни зубов
Болезни зубов Федеральная программа пенсионного обеспечения работников государственного сектора
Федеральная программа пенсионного обеспечения работников государственного сектора маркетинг в здравоохранении
маркетинг в здравоохранении  Применение параллельной записи
Применение параллельной записи Витамины и здоровье
Витамины и здоровье Презентация на тему Тайга
Презентация на тему Тайга Классный час по теме: "Конфликт и пути его решения"
Классный час по теме: "Конфликт и пути его решения" Архитектура 18 века Барокко
Архитектура 18 века Барокко Старые процессоры AMD
Старые процессоры AMD Презентация на тему Значение и охрана птиц
Презентация на тему Значение и охрана птиц Добро пожаловать на урок!
Добро пожаловать на урок!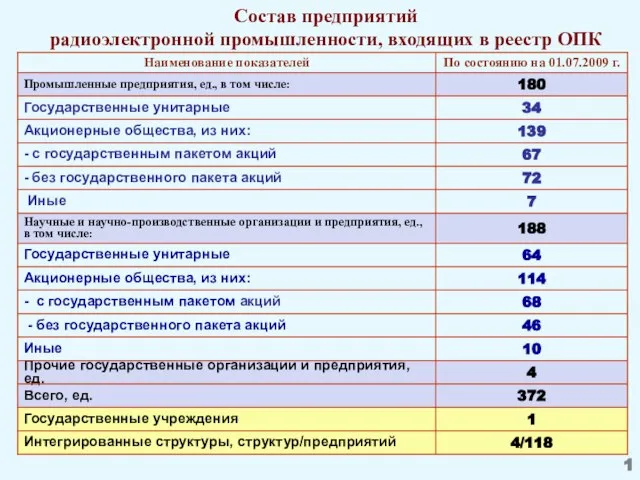 Состав предприятий радиоэлектронной промышленности, входящих в реестр ОПК
Состав предприятий радиоэлектронной промышленности, входящих в реестр ОПК Новый год: история и традиции
Новый год: история и традиции шестьдесят
шестьдесят Тип Круглые червиВид Аскарида человеческая
Тип Круглые червиВид Аскарида человеческая Наука в СССР
Наука в СССР Городу 55! Проспект Победы на 5!
Городу 55! Проспект Победы на 5! Центр экспериментальной хирургии
Центр экспериментальной хирургии Приключения Флоры
Приключения Флоры Развитие критического мышления для формирования мыслительной деятельности
Развитие критического мышления для формирования мыслительной деятельности