Содержание
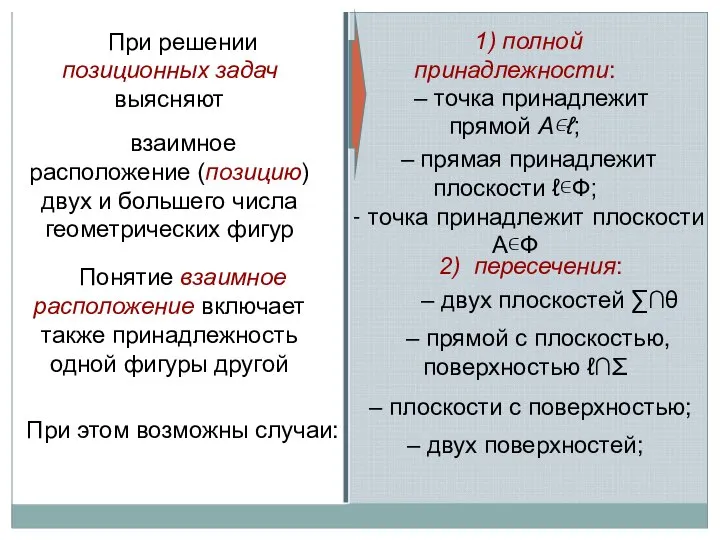
- 2. При решении позиционных задач выясняют взаимное расположение (позицию) двух и большего числа геометрических фигур Понятие взаимное
- 3. Две геометрические фигуры, пересекаясь, дают общий элемент: Прямая с прямой – точку (а∩b⇒К) Прямая с плоскостью
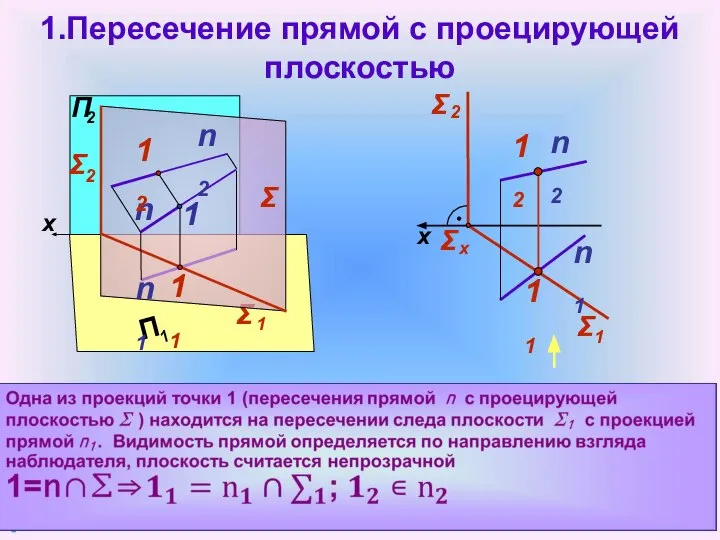
- 4. Σ 1.Пересечение прямой с проецирующей плоскостью n2
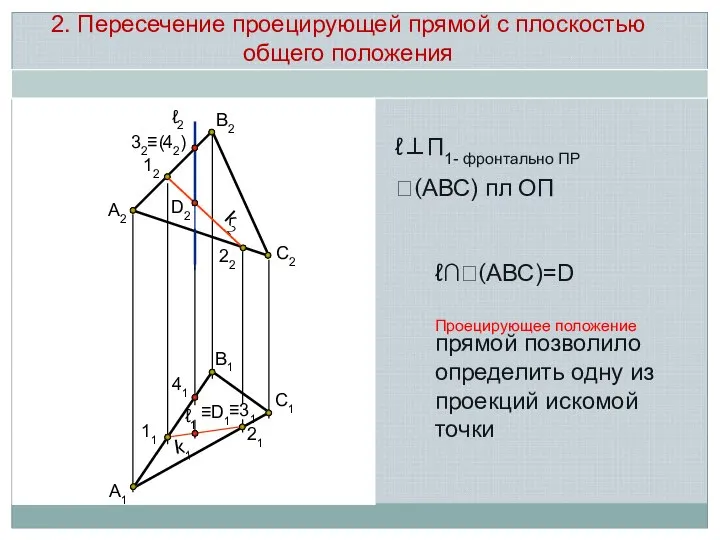
- 5. А2 В2 С2 12 22 D2 А1 С1 В1 21 11 ℓ2 k2 2. Пересечение проецирующей
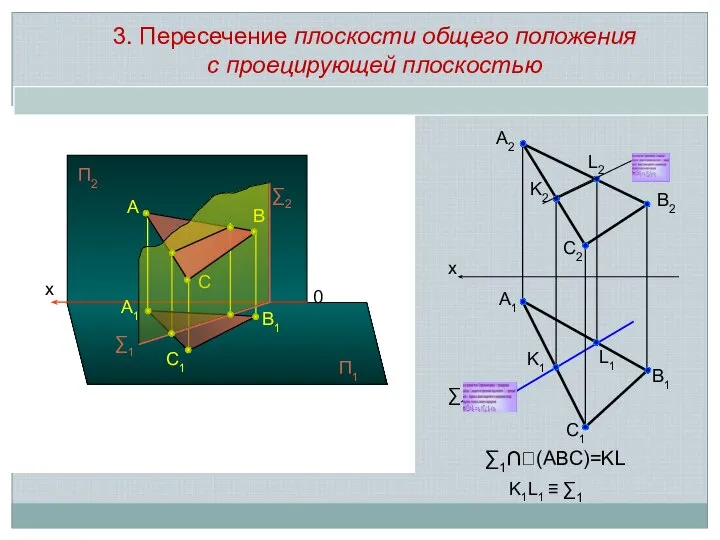
- 6. x A1 C1 B1 A 0 B C x ∑1 ∑2 ∑1 А1 А2 В1 С1
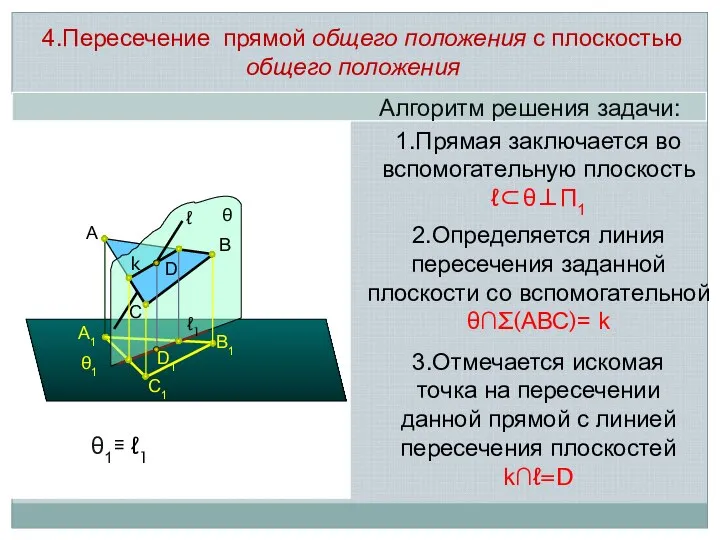
- 7. Алгоритм решения задачи: A1 C1 B1 A D1 1.Прямая заключается во вспомогательную плоскость ℓ⊂θ⊥П1 ℓ θ1
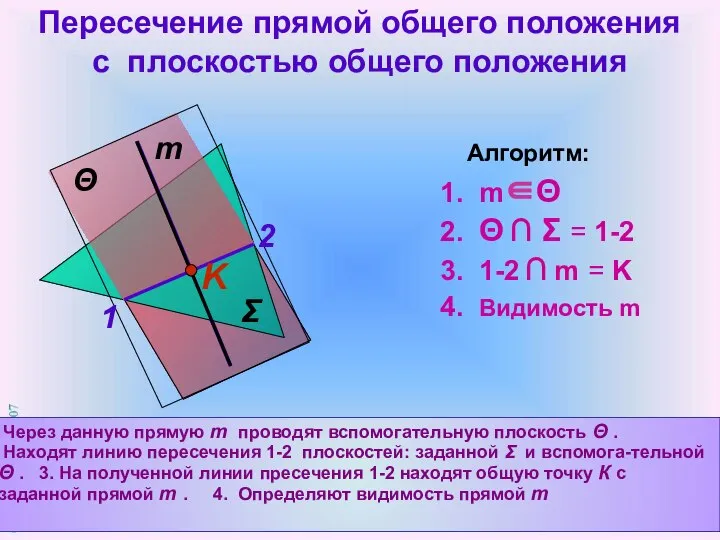
- 8. Пересечение прямой общего положения с плоскостью общего положения Σ m Через данную прямую m проводят вспомогательную
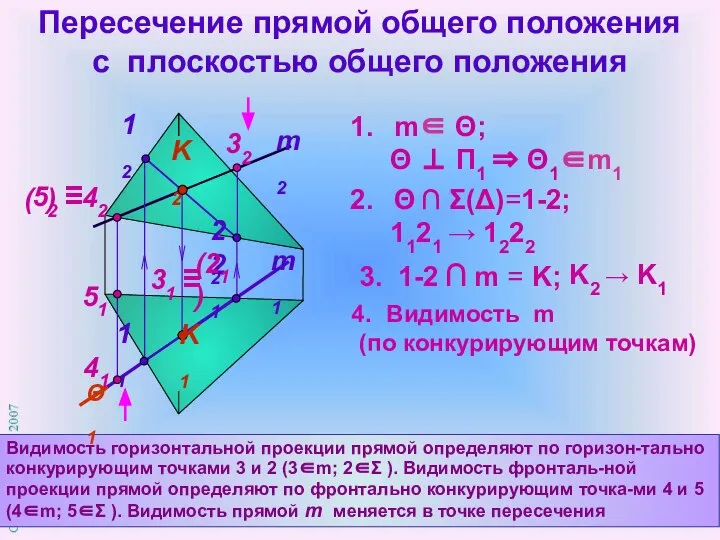
- 9. Пересечение прямой общего положения с плоскостью общего положения m1 m2 Видимость горизонтальной проекции прямой определяют по
- 10. Частный случай способа вспомогательных секущих поверхностей Используется для решения позиционных задач Секущие плоскости выбирают так, чтобы
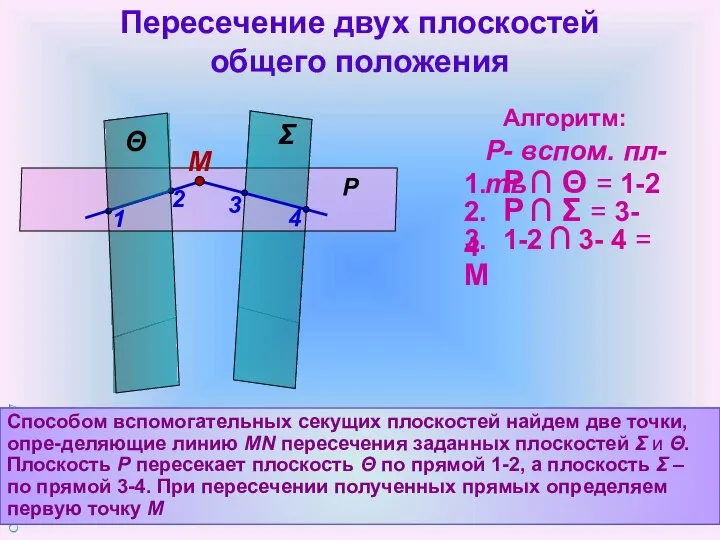
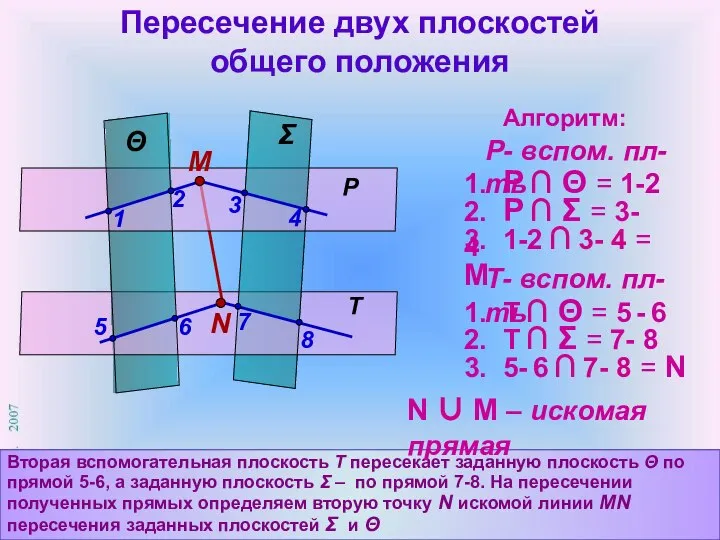
- 11. Пересечение двух плоскостей общего положения Способом вспомогательных секущих плоскостей найдем две точки, опре-деляющие линию MN пересечения
- 12. Пересечение двух плоскостей общего положения Вторая вспомогательная плоскость Т пересекает заданную плоскость Θ по прямой 5-6,
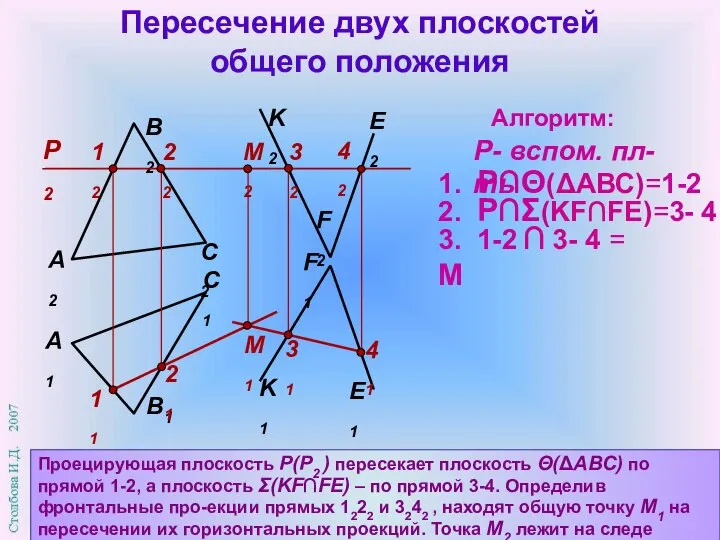
- 13. Пересечение двух плоскостей общего положения Алгоритм: 2. P∩Σ(KF∩FE)=3- 4 3. 1-2 ∩ 3- 4 = M
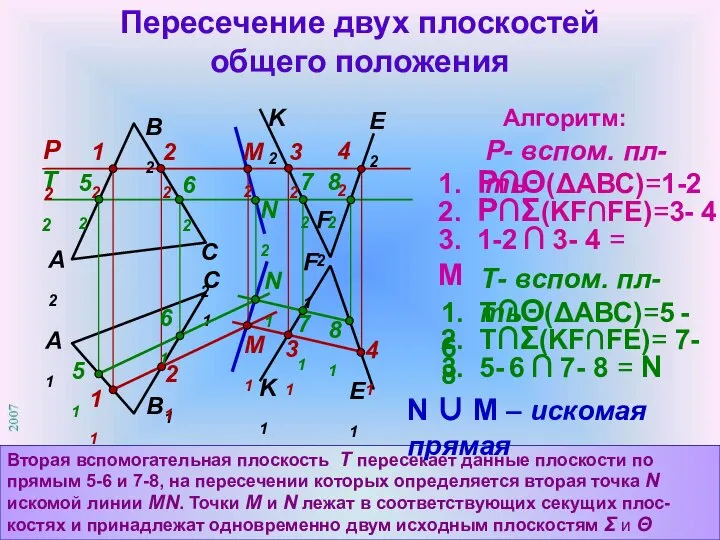
- 14. Пересечение двух плоскостей общего положения Вторая вспомогательная плоскость Т пересекает данные плоскости по прямым 5-6 и
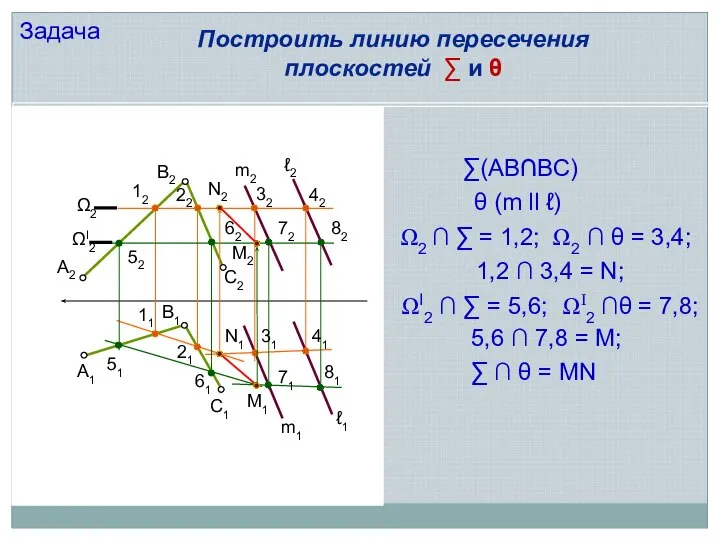
- 15. А2 В2 С2 С1 В1 А1 m2 m1 ℓ1 ℓ2 Ω2 ΩI2 12 22 32 42
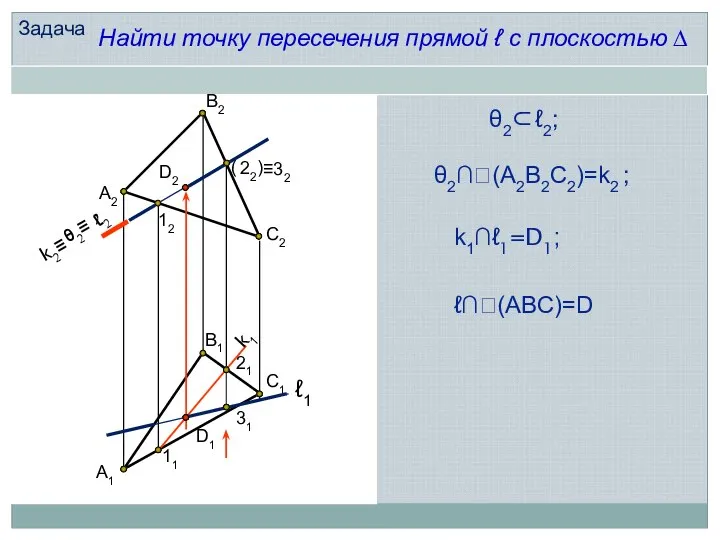
- 16. А2 В2 С2 12 22 D2 А1 С1 В1 21 11 D1 ℓ2 θ2≡ k2≡ k1
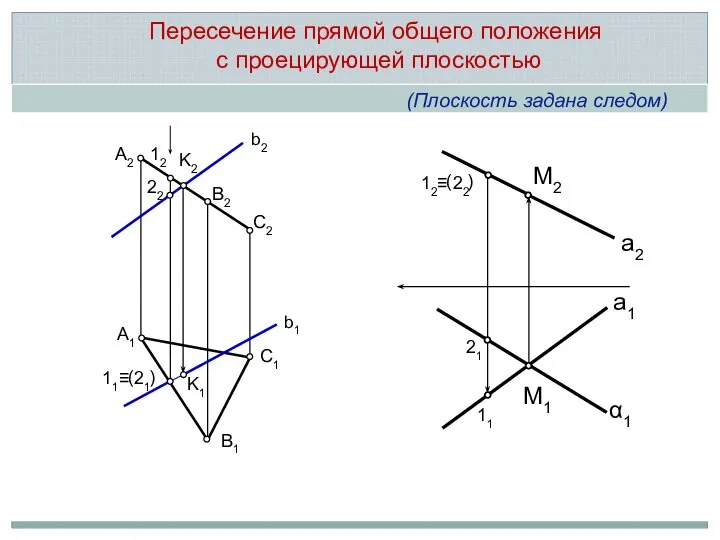
- 17. 11≡ 21 ( ) A2 B2 C2 C1 B1 A1 22 12 K2 K1 b1 b2
- 19. Скачать презентацию


 Межшкольное методическое объединениеучителей русского языка и литературы
Межшкольное методическое объединениеучителей русского языка и литературы Родные горы, родной Кавказ
Родные горы, родной Кавказ Налог. Налогообложение
Налог. Налогообложение Искусство моих земляков. Фотоальбом
Искусство моих земляков. Фотоальбом Горох Менделя
Горох Менделя Цвет и композиция в натюрморте
Цвет и композиция в натюрморте Лесозаготовительные и лесопильные средства мостостроительных подразделений. (Тема 4.2)
Лесозаготовительные и лесопильные средства мостостроительных подразделений. (Тема 4.2) Санкт-Петербург. Мосты Санкт-Петербурга
Санкт-Петербург. Мосты Санкт-Петербурга Презентация на тему Соглашение об упрощении процедур торговли ВТО (Аgreement on trade facilitation)
Презентация на тему Соглашение об упрощении процедур торговли ВТО (Аgreement on trade facilitation)  Инструменты Стратегического планирования
Инструменты Стратегического планирования Тема урока: «Численность и воспроизводство населения мира»
Тема урока: «Численность и воспроизводство населения мира» «Доступность пригородного железнодорожного сообщения в регионах Российской Федерации»
«Доступность пригородного железнодорожного сообщения в регионах Российской Федерации» Названия фруктов и овощей в английском
Названия фруктов и овощей в английском Прослушивание стихотворения С.Есенина «Поет зима,аукает»
Прослушивание стихотворения С.Есенина «Поет зима,аукает» Мобильный телефон друг или враг человека
Мобильный телефон друг или враг человека Политические партии и движения
Политические партии и движения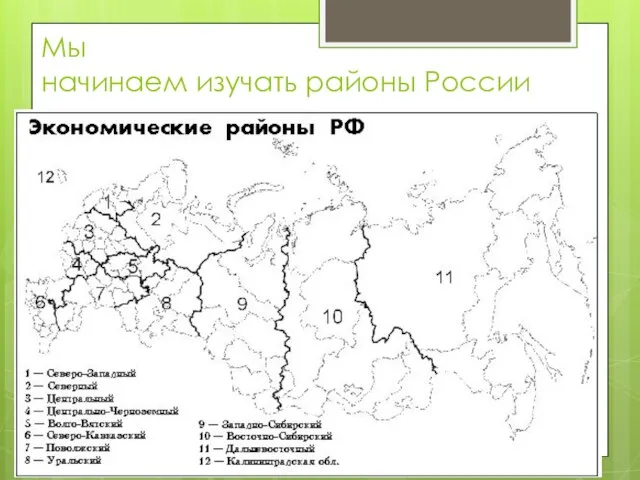 Мы начинаем изучать районы России
Мы начинаем изучать районы России Реконструкция ул. Бударина и Набережной Оми Напастюк
Реконструкция ул. Бударина и Набережной Оми Напастюк Николай Георгиевич Гарин-Михайловский 1852-1906
Николай Георгиевич Гарин-Михайловский 1852-1906 Путешествие по стране дорожных знаков
Путешествие по стране дорожных знаков Geography of great britain
Geography of great britain Презентация на тему Повторение гласных звуков и букв
Презентация на тему Повторение гласных звуков и букв  Педагогический совет
Педагогический совет The soul cannot live without love!
The soul cannot live without love! Идеи Раскольникова
Идеи Раскольникова МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ ДЕТЕЙ «ДЕТСКО – ЮНОШЕСКАЯ СПОРТИВНАЯ ШКОЛА"
МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ ДЕТЕЙ «ДЕТСКО – ЮНОШЕСКАЯ СПОРТИВНАЯ ШКОЛА" ТЕХНИЧЕСКОЕ ЗАДАНИЕ
ТЕХНИЧЕСКОЕ ЗАДАНИЕ Придаточные предложения места
Придаточные предложения места