Содержание
- 2. 1. Постановки и основные методы решения базовых задач обоснования решений 2. Многокритериальный выбор и оценочные системы
- 3. Вербальная постановка задачи удобна для содержательного анализа и выбора подхода к решению проблемы. Она также незаменима
- 4. Следование такому порядку формализации вербальной задачи позволяет эффективно концентрировать внимание на сущности каждого из логически обусловленных
- 5. Многокритериальный выбор и оценочные системы. Значительная роль при проведении процедур многокритериального экспертного оценивания принадлежит оценочным системам.
- 6. Структура оценочной системы Оценочная система, используемая при многокритериальном экспертном оценивании, включает такие важные составляющие, как: перечень
- 7. Формирование перечня критериев Перечень критериев, характеризующих сравнительную предпочтительность объектов принятия управленческого решения, должен удовлетворять ряду естественных
- 8. Оценка сравнительной важности критериев Один из широко используемых методов сравнительной оценки многокритериальных объектов принятия управленческих решений
- 9. Шкала для оценки проектов по критериям Нередко для оценивания проектов возникает необходимость в использовании критериев, оценки
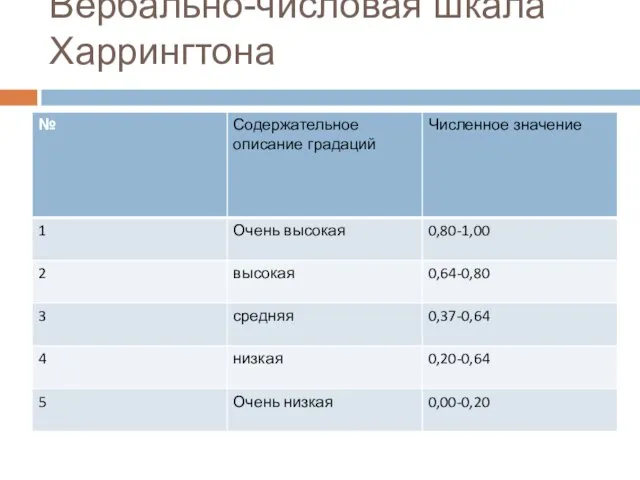
- 10. Вербально-числовая шкала Харрингтона
- 11. Методы получения экспертных оценок Остановимся теперь на основных способах экспертных измерений — методах получения экспертных оценок,
- 12. Методы получения количественных экспертных оценок Непосредственная экспертная оценка Метод средней точки Метод Чермена – Акофа Метод
- 13. Непосредственная экспертная оценка Непосредственная количественная оценка используется как в случае, когда надо определить значение показателя, измеряемого
- 14. Если эксперт затрудняется указать конкретное значение показателя, он может указать диапазон, в котором лежит значение оцениваемого
- 15. Метод средней точки Метод может быть использован при экспертной оценке численных значений показателей, имеющих количественный характер
- 16. Например для расчета эластичности спроса и предложения по средней точке на отрезке кривой спроса и предложения.
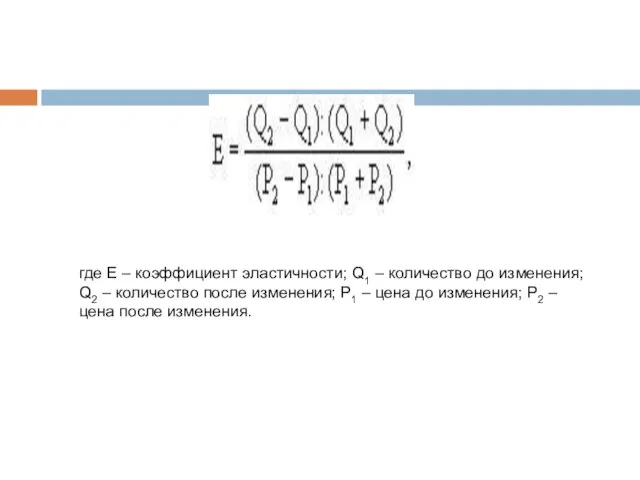
- 17. где E – коэффициент эластичности; Q1 – количество до изменения; Q2 – количество после изменения; P1
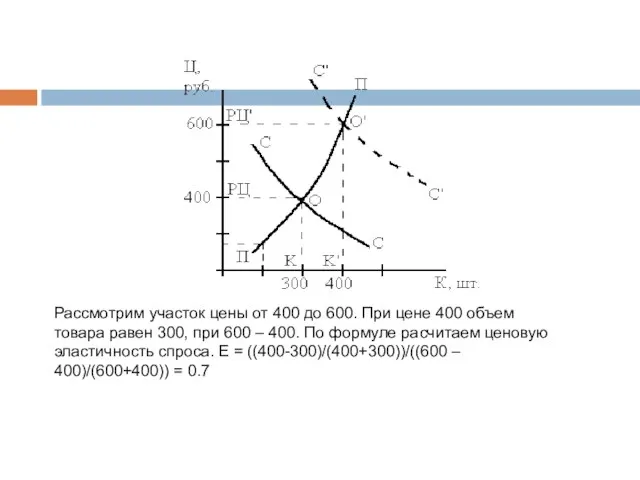
- 18. Рассмотрим участок цены от 400 до 600. При цене 400 объем товара равен 300, при 600
- 19. Метод Черчмена-Акофа Этот метод относится к числу наиболее популярных при оценке альтернатив. В нем предполагается последовательная
- 20. Согласно методу Черчмена-Акоффа альтернативы a1, а2, ... aN ранжируются по предпочтительности. Пусть для удобства изложения альтернатива
- 21. Если альтернатива а1 оказывается менее предпочтительной, то для уточнения оценок она сравнивается по предпочтению с суммой
- 22. Пример: В ходе анализа финансового состояния организации было выявлено, что уровень рентабельности недостаточно высок, доля собственных
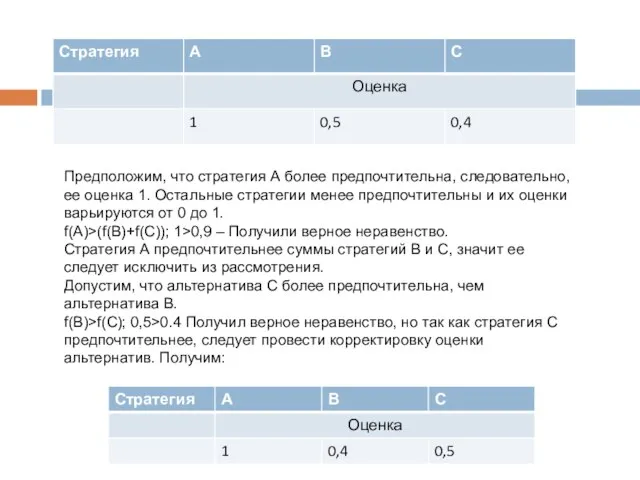
- 23. Предположим, что стратегия А более предпочтительна, следовательно, ее оценка 1. Остальные стратегии менее предпочтительны и их
- 24. Метод лотерей В соответствии с методом имеющиеся альтернативы распределяются в порядке убывания предпочтительности, для обозначения которой
- 25. Рассмотрим этот метод на предыдущем примере. Допустим, что альтернатива А может случится с вероятностью р=0,4, тогда
- 26. Методы получения качественных экспертных оценок Иногда специфика объектов экспертного оценивания такова, что эксперты затрудняются дать количественные
- 27. Экспертная классификация Используется, когда необходимо определить принадлежность оцениваемых вариантов решений к установленным и принятым к использованию
- 28. Если эксперту необходимо отнести каждый из вариантов к одному из заранее установленных классов, то наиболее распространена
- 29. Если проводится коллективная экспертиза, то результаты экспертной классификации, полученные каждым из экспертов, обрабатываются с целью получения
- 30. Если число классов, на которое должны быть разбиты альтернативные варианты, заранее не оговаривается, то целесообразно использование
- 31. Метод парных сравнеий Эксперту последовательно предлагаются пары вариантов, из которых он должен указать более предпочтительный. Если
- 32. В практике использования метода парных сравнений нередко приходится сталкиваться с непоследовательностью и даже противоречивостью оценок эксперта.
- 33. Ранжирование альтернативных вариантов Эксперту предъявляются отобранные для сравнительной оценки варианты, но желательно не более 20-30 для
- 34. Ранжирование сравниваемых объектов эксперт может осуществлять различными способами. Например, эксперту предъявляется весь набор вариантов, и он
- 35. Метод векторных предпочтений Этот метод чаще используется при необходимости получения коллективного экспертного ранжирования. Эксперту предъявляется весь
- 36. Если в векторе предпочтений каждое число встречается ровно один раз, то экспертом указано строгое ранжирование альтернативных
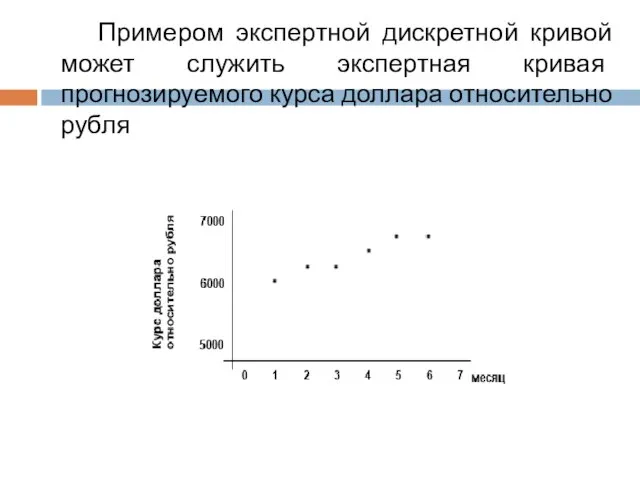
- 37. Экспертные дискретные кривые Используется в случаях, когда разрабатываются прогнозы или анализируется динамика изменения показателей, характеризующих объект
- 38. Если есть достаточно веские основания для того, чтобы определить нелинейные изменения на участках кривой между соседними
- 39. Использование экспертных кривых позволяет более наглядно и надежно представить различные сценарии развития ситуации, что часто бывает
- 40. Примером экспертной дискретной кривой может служить экспертная кривая прогнозируемого курса доллара относительно рубля
- 41. Задача измерения Вся деятельность ЛПР объективно сводится к непрерывному решению, по сути, только одной задачи —
- 42. Решать эту задачу следует как можно более эффективно. На практике это означает неукоснительное следование только одному
- 43. Для осмысленного, рационального выбора способа измерения следует глубже разобраться в свойствах разных типов шкал. Шкала –
- 44. Шкалирование — это операция упорядочивания исходных эмпирических данных путем перевода их в шкальные оценки. Шкала дает
- 45. В исследованиях применяют классификацию шкал, предложенную С.Стивенсоном, согласно которой четыре основных способа измерения, связанные с различными
- 46. Номинальная шкала Самой слабой качественной шкалой является номинальная (шкала наименований, классификационная шкала), по которой объектам х.
- 47. Шкалы номинального типа допускают только различение объектов на основе проверки выполнения отношения равенства на множестве этих
- 48. Ранговая шкала Шкала называется ранговой (шкала порядка), если множество Ф состоит из всех монотонно возрастающих допустимых
- 49. 1. необходимо упорядочить объекты во времени или пространстве. Это ситуация, когда интересуются не сравнением степени выраженности
- 50. Примером может служить шкала Рихтера. Шкала Рихтера — классификация землетрясений по магнитудам, основанная на оценке энергии
- 51. Шкалы интервалов Одним из наиболее важных типов шкал является тип интервалов. Тип шкал интервалов содержит шкалы,
- 52. Шкала отношения Шкалой отношений (подобия) называется шкала, если Ф состоит из преобразований подобия ср (х) =
- 53. Задача получения информации для анализа условий и выявления ''механизма ситуации" Рассмотрим задачу, моделирующую третий и четвертый
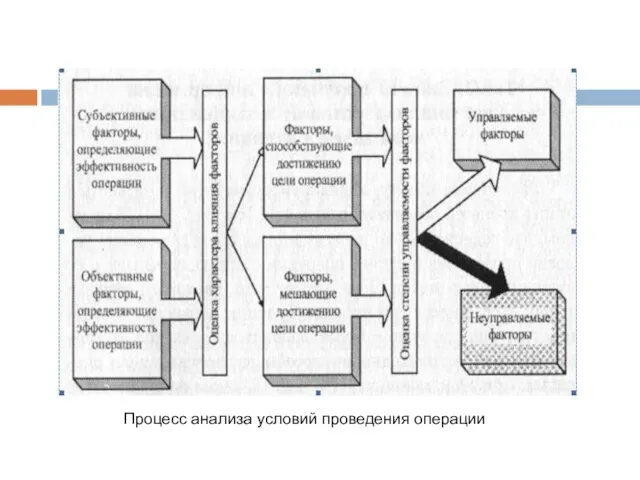
- 54. Процесс анализа условий проведения операции
- 55. После этого ЛПР останется "только решить", как воздействовать на управляемые факторы, чтобы ослабить отрицательное влияние мешающих
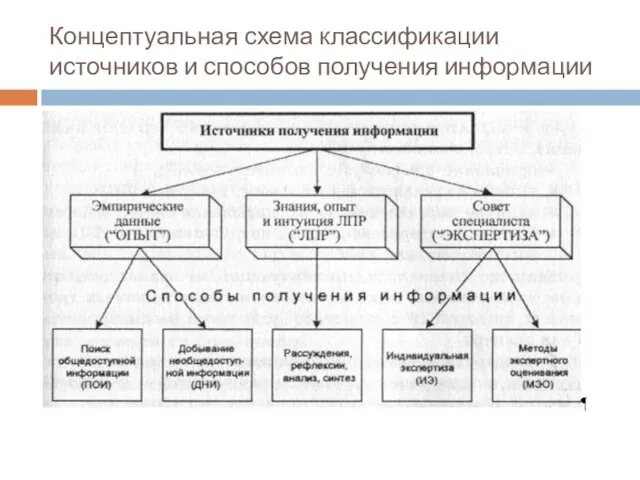
- 56. Концептуальная схема классификации источников и способов получения информации
- 57. В любой постановке задачи важно правильно выбрать источник и установить способ получения необходимой информации. Для того
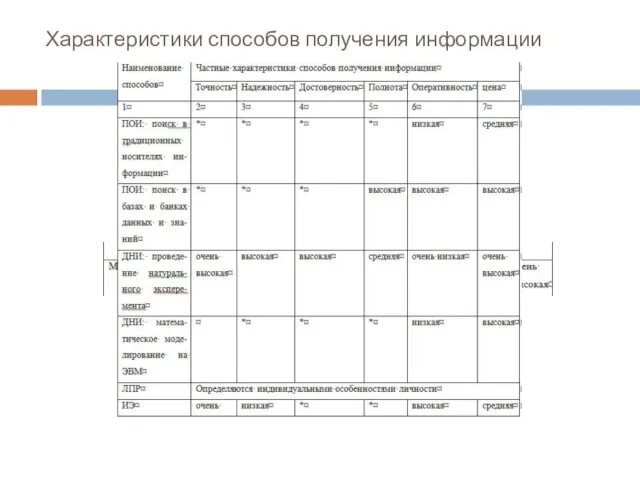
- 58. Характеристики способов получения информации
- 59. Под точностью информации будем понимать степень близости содержащихся в ней данных тем, какие объективно присутствуют в
- 60. При анализе табллицы важно иметь в виду следующее. В некоторых ячейках таблицы помещен специальный символ *.
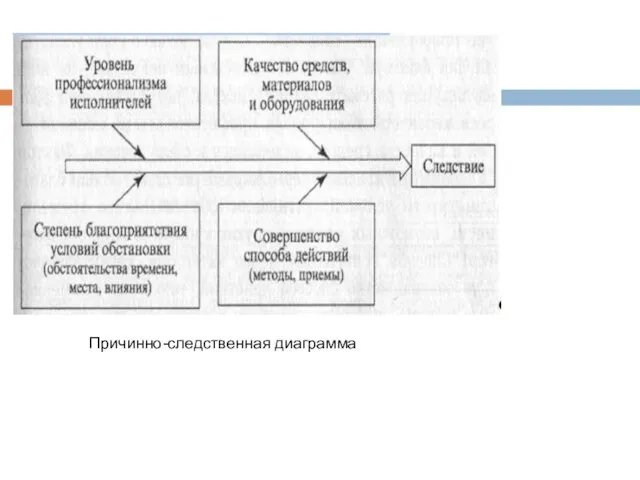
- 61. Планирование процесса сбора информации удобно осуществлять с помощью причинно-следственной диаграммы. Диаграмма моделирует, как из основных факторов
- 62. Причинно-следственная диаграмма
- 63. Задача формирования исходного множества альтернатив Во-первых, множество альтернатив должно быть по возможности более широким. Это обеспечит
- 64. В случаях детерминированного, стохастического или природно-неопределенного "механизмов ситуации" методика формирования исходного множества альтернатив предполагает совершение достаточно
- 65. Полученное в ходе инженерного или оперативного синтеза множество вариантов решения проблемы назовем множеством "целевых альтернатив". После
- 66. Что касается технологических приемов реализации представленной общей методики формирования исходного множества альтернатив, то здесь все зависит
- 67. Для целостного и единого ее понимания воспользуемся тремя основными понятиями: "важное обстоятельство", "измеримая характеристика", "финальный" элемент.
- 68. Если дерево целей строится на основе анализа "желаемого" состояния, процедуру ветвления удобнее отображать графически. Результат построения
- 69. Наконец, следует иметь в виду, что все полученные методом дерева решений варианты могут быть взаимоисключающими или
- 70. Метод морфологических таблиц Метод морфологических таблиц, с одной стороны, представляет определенную модификацию метода дерева решений. С
- 71. Задача моделирования предпочтений. Основные модели предпочтений Пусть теперь результаты у(а, s) для каждой из альтернатив получены.
- 72. Вербальная постановка задачи моделирования предпочтений задается следующими высказываниями. Дано: Описание цели операции, условий ее проведения, сведения
- 73. В дальнейшем будем полагать, что ЛПР может сравнить между собой любые два элемента d. и d.
- 74. Мы же дадим краткую характеристику некоторых наиболее распространенных приемов. К ним относят сортировку, попарное сравнение, ранжирование
- 75. Сортировка ЛПР должно разделить элементы множества предъявления на некоторые предложенные классы. Например, множество возможных сценариев развития
- 76. Попарное сравнение Попарное сравнение — сравнительно простой способ выявления элементарных предпочтений. Чаще всего при попарном сравнении
- 77. Ранжирование Это способ выражения предпочтений, заключающийся в расположении предъявленных элементов в порядке возрастания (так называемое прямое
- 78. Бальное оценивание Оно заключается в том, что каждому элементу из множества предъявленных ставят в соответствие число
- 80. Скачать презентацию




































































 Презентация на тему Задачи на смеси и сплавы (9 класс)
Презентация на тему Задачи на смеси и сплавы (9 класс) Русская литература XX века: общая характеристика
Русская литература XX века: общая характеристика Денежные единицы мира
Денежные единицы мира Презентация на тему Золотой век Екатерины II
Презентация на тему Золотой век Екатерины II  Доходный подход к оценке
Доходный подход к оценке Музей Конфлуанс
Музей Конфлуанс Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ
Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ Презентация на тему Технология обработки древесины
Презентация на тему Технология обработки древесины Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье
Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье Поняття ЕТ Excel
Поняття ЕТ Excel Налоги: сущность и виды. Классификация
Налоги: сущность и виды. Классификация Внутреняя энергия
Внутреняя энергия В стране правовых знаний
В стране правовых знаний Убранство русской избы
Убранство русской избы Политико-правовая теория Монтескье
Политико-правовая теория Монтескье 169601
169601 Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол
Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол Франсуа Виет и его теорема (8 класс)
Франсуа Виет и его теорема (8 класс) Может ли природа жить без человека?
Может ли природа жить без человека? Юридическая ответственность и её виды
Юридическая ответственность и её виды Осенняя одежда
Осенняя одежда Банк внешней торговли (Внешторгбанк)
Банк внешней торговли (Внешторгбанк)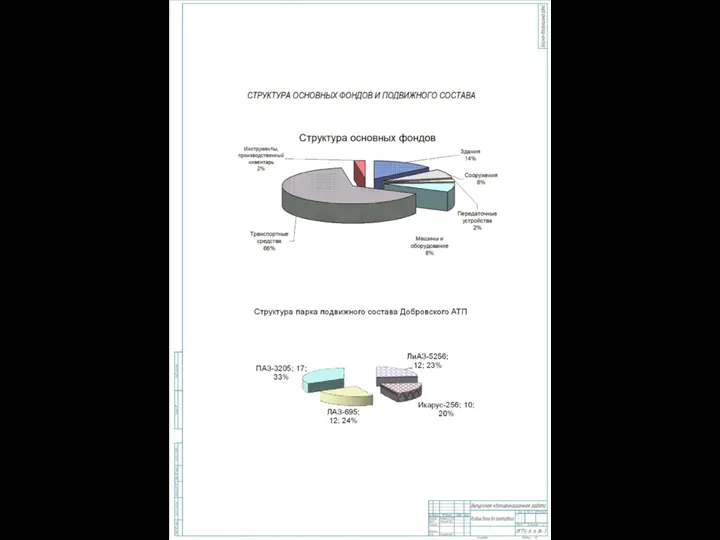 Структура основных фондов и подвижного состава
Структура основных фондов и подвижного состава Saint Isaac’s Square
Saint Isaac’s Square Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.
Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.  Педагогический совет
Педагогический совет Виды Смоленска
Виды Смоленска НАСС
НАСС