Содержание
- 2. Содержание. 1.Определение функции заданной неявно. 2.Определение лемнискаты. 3.Вывод уравнения лемнискаты. 4.Преобразование уравнения лемнискаты. 5.Уравнение лемнискаты в
- 3. Определение неявно заданной функции Рассмотрим функцию, заданную неявно уравнением F(x ,y)=0. В зависимости от того, какой
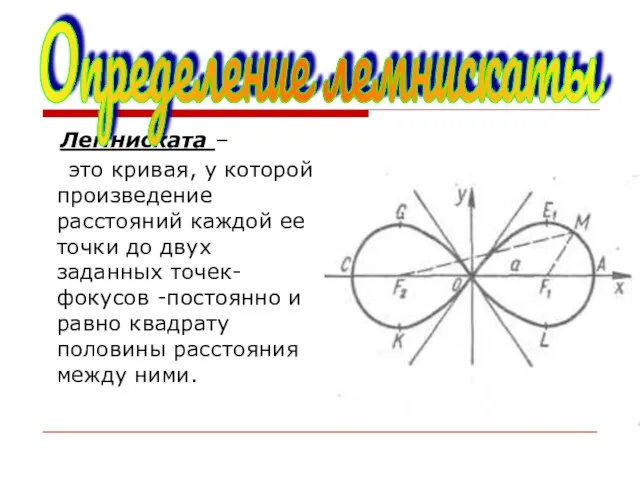
- 4. Лемниската – это кривая, у которой произведение расстояний каждой ее точки до двух заданных точек- фокусов
- 5. Пусть фокусы имеют координаты: F1(-a;0) и F2 (а;0); М(х, у) - произвольная точка геометрического места, то
- 6. Преобразование уравнения лемнискаты Дальнейшая цель- получить уравнение лемнискаты Бернулли в более простом виде. Возводя в квадрат
- 7. Преобразование уравнения лемнискаты Преобразуя последнее уравнение, имеем: или в окончательном виде Мы получили уравнение лемнискаты в
- 8. Построение графика лемнискаты Т.к х и у входят в это уравнение только в чётных степенях, то
- 9. Уравнение лемнискаты в полярной системе координат Поскольку х =ρ cos φ, у = ρ sinφ, х2+у2=
- 10. ρ 2=2а2 cos2φ Из этого уравнения видно, что при φ=0. Если φ увеличивается в пределах от
- 11. Построение лемнискаты Построим график функции при разных значениях а: при а=1
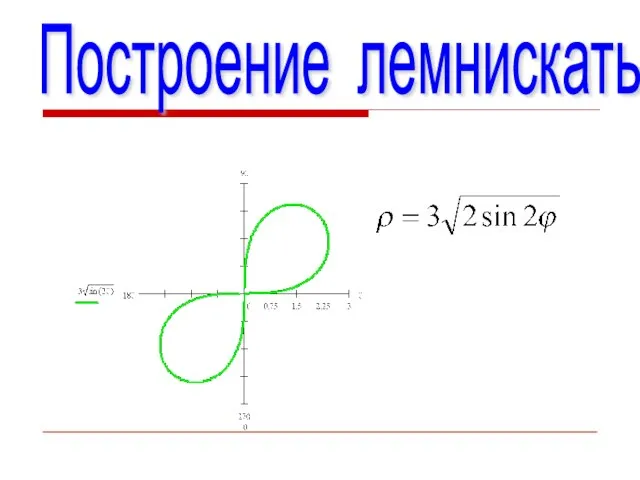
- 12. Построение лемнискаты
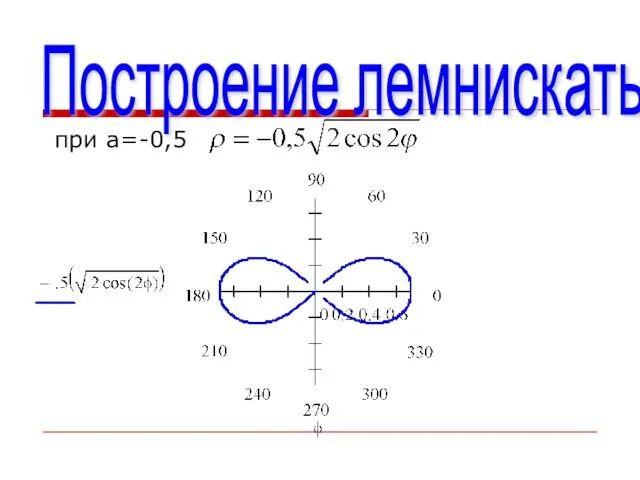
- 13. Построение лемнискаты при а=-0,5
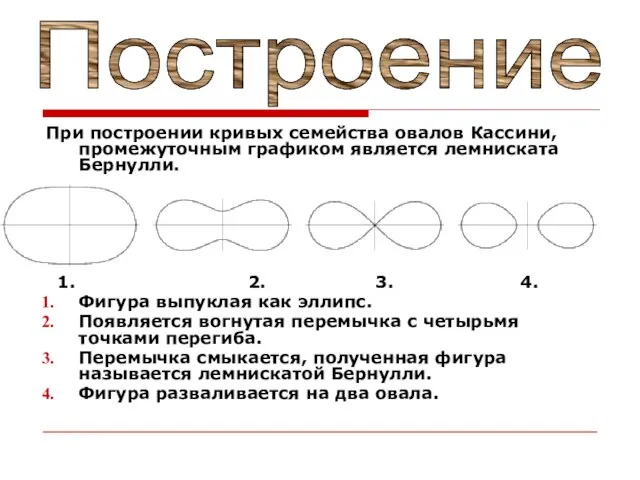
- 14. При построении кривых семейства овалов Кассини, промежуточным графиком является лемниската Бернулли. 1. 2. 3. 4. Фигура
- 15. В технике лемниската применяется, в частности, в качестве переходной кривой на закруглениях малого радиуса, как это
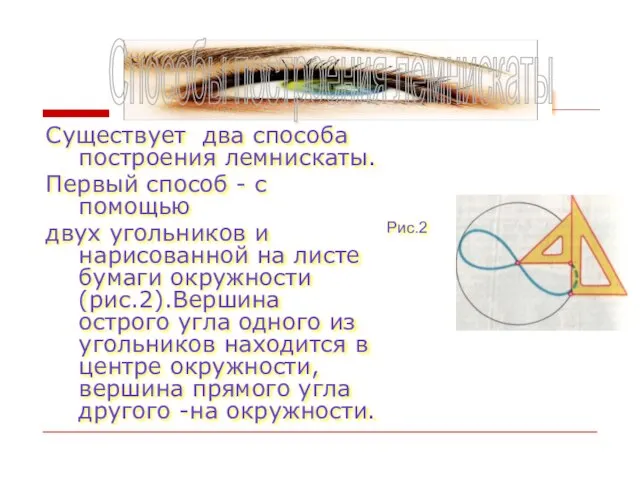
- 16. Существует два способа построения лемнискаты. Первый способ - с помощью двух угольников и нарисованной на листе
- 17. Второй способ - с помощью шарнирного устройства, две точки которого закреплены на плоскости (рис.3). Способы построения
- 18. Лемниската Бернулли. Ее автор – швейцарский математик Якоб Бернулли. Он дал этой кривой поэтическое название «лемниската».
- 19. БЕРНУЛЛИ Якоб I (1654-1705). Швейцарский математик. Работал в Базельском университете. Работы посвящены математическому анализу, теории вероятностей
- 20. ♣ Вирченко Н.А. и др.Справочник «Графики функций»; Киев: Наук. думка, 1979г; ♣ И.И.Валуцэ «Математика для техникумов»;
- 22. Скачать презентацию














 Виды измерительных приборов для создания интерьера
Виды измерительных приборов для создания интерьера Композиция и пространственное моделирование. Масштабность. (Лекция 4)
Композиция и пространственное моделирование. Масштабность. (Лекция 4) ТестФизика элементарных частиц
ТестФизика элементарных частиц Художественный мир Макото Синкая
Художественный мир Макото Синкая Организация работы и расчет экономических показателей участка механической обработки детали типа Корпус
Организация работы и расчет экономических показателей участка механической обработки детали типа Корпус У М К "Г а р м о н и я"
У М К "Г а р м о н и я" Инструкция по обновлению ПО в Huawei MMC255
Инструкция по обновлению ПО в Huawei MMC255 Проект Званый ужин
Проект Званый ужин Информация и расчеты для инженерной системы. Персональное решение
Информация и расчеты для инженерной системы. Персональное решение Английская литература XIX века
Английская литература XIX века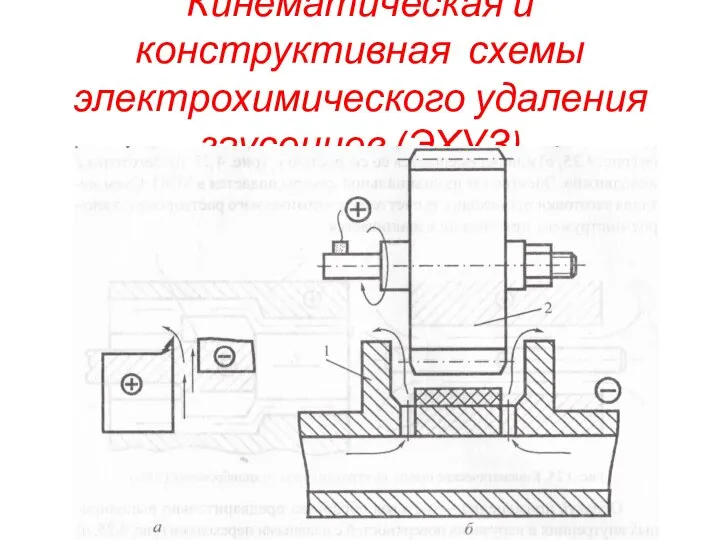 Кинематическая и конструктивная схемы электрохимического удаления заусенцев (ЭХУЗ)
Кинематическая и конструктивная схемы электрохимического удаления заусенцев (ЭХУЗ) Стихотворные размеры
Стихотворные размеры Лот 2, г. Хабаровск, ул. Сысоева, 21, кв. 6
Лот 2, г. Хабаровск, ул. Сысоева, 21, кв. 6 Питание и пищеварение
Питание и пищеварение Информационные технологии
Информационные технологии  Презентация на тему: Past Progressive
Презентация на тему: Past Progressive Разработка мероприятия Цифровой текстиль. Синтетические ткани
Разработка мероприятия Цифровой текстиль. Синтетические ткани Занимательные задачки
Занимательные задачки Условные графические изображения строительных конструкций и их элементов, санитарно-технических устройств
Условные графические изображения строительных конструкций и их элементов, санитарно-технических устройств Презентация на тему Кижи
Презентация на тему Кижи Цирроз печени и его осложнения
Цирроз печени и его осложнения Методическое обеспечение учебно-воспитательного процесса как условие реализации ООП бакалавриата в Московском государственно
Методическое обеспечение учебно-воспитательного процесса как условие реализации ООП бакалавриата в Московском государственно Несколько слов к вопросу о том, можно ли улучшить использование электронных ресурсов..
Несколько слов к вопросу о том, можно ли улучшить использование электронных ресурсов.. Управление персоналом
Управление персоналом Презентация на тему Шаманы северных народов
Презентация на тему Шаманы северных народов  Представители разных слоев общества в литературе: маргиналы, люмпены, отшельники, нувориши
Представители разных слоев общества в литературе: маргиналы, люмпены, отшельники, нувориши Лес - природное сообщество (3 класс)
Лес - природное сообщество (3 класс) Всегда ли мы удовлетворены, тем что происходит в школе ? Очевидно, не всегда и не во всем. Можем ли мы повлиять на это ? Как устроена ж
Всегда ли мы удовлетворены, тем что происходит в школе ? Очевидно, не всегда и не во всем. Можем ли мы повлиять на это ? Как устроена ж