Построение графиков функций сложных функций на основе свойств монотонности

Графики сложных функций вида y=f (v (x)) легко построить, зная свойства основных элементарных функций
вида y=f (x).
гипотеза
Выработаем
простой алгоритм построения графиков.

1. Область определения/
область значения функций
2. Четность/нечетность
функций
3. Монотонность функций
основные свойства функций
ДЛЯ ЭТОГО ВСПОМНИМ

Симметричное отображение
Параллельный перенос
Растяжение
Сжатие
и преобразования графиков

к построению
П Р И С Т У П И М
графиков сложных функций
вида y=f (v (x)).

Сложная функция (четная).
x
v
v
x
y
y
0
0
0
1
1
1
1
1
0,5
-1
-1
1
V=1+х2
Y=1/V
Контрольные точки: (1;0,5), (-1;0,5).
-1
-1

Сложная функция y=arctg 2x
x
v
v
x
y
y
0
0
0
1
1
1
∏/2
-1
1
V= 2x
Y=arctg V
Контрольные точки: (0;∏/4).
∏/2
-1
-∏/2
∏/4
1/2
-1

Сложная функция y=arctg 1/x, х=0
x
v
v
x
y
y
0
0
0
1
1
1
∏/2
√3
-1
-1
1
V=1/X
Y=arctg V
Контрольные точки: (1;∏/4), (√3;∏/6).
∏/2
-1
-∏/2
-∏/2
∏/4
- ∏/4
∏/6

Таким образом я построил графики сложных функций:
x
x
y
0
0
0
1
1
∏/2
-1
1
Y=2 1/х
Y=arctg lnх
1/2
-1
-∏/2
∏/2
∏/4
- ∏/2
3∏/2
y
x
2
1/2
-3
3
3
Y=ln (x2-3х+2)
x
y
0
1
-1
2/∏
- 4/∏
Y=1/arctg х,
D (y)=(-∞;0) U (0;+∞)
y
y
2
1
0
x
Y= 2 sinх

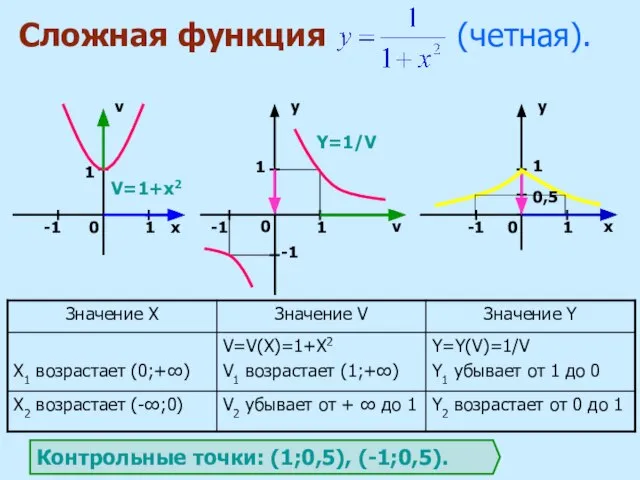
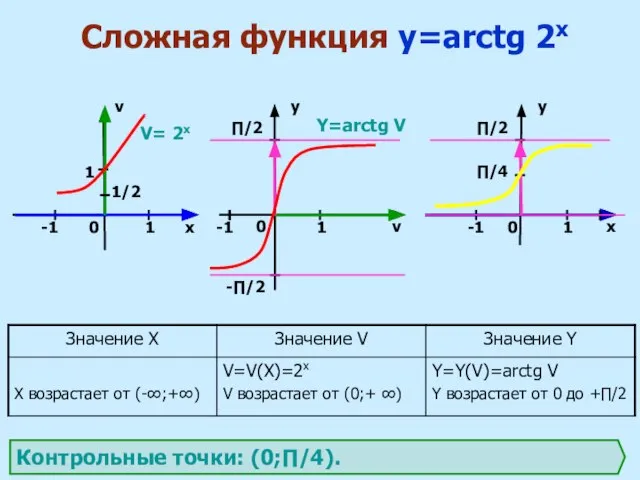
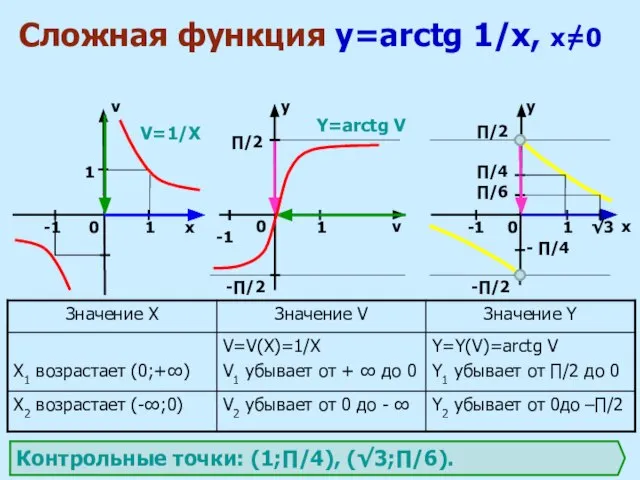
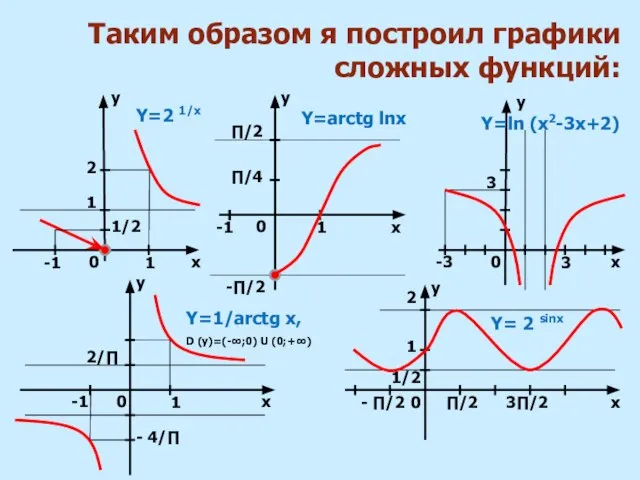
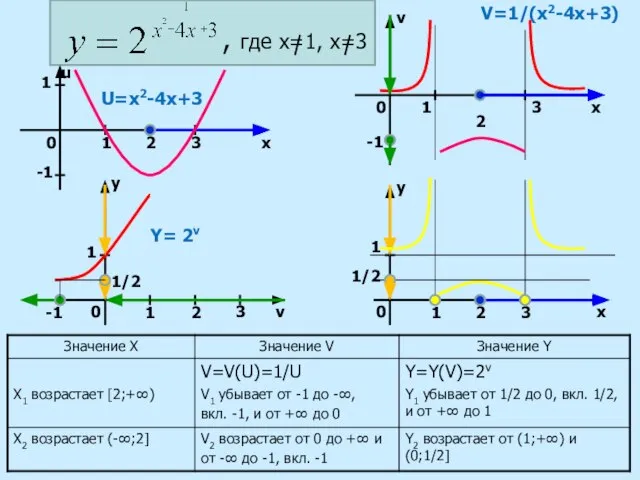
1. начертить графики внутренней v = v(x) и внешней y = f (v) функций и систему координат XOY.
6. построить график сложной функции y = y (x) в системе координат XOY с учетом промежутков монотонности Х, Y и контрольных точек.
2. определить промежутки монотонности внутренней функции v = v (x).
4. на каждом промежутке определить границы изменения функции v = v(x) и выбрать те значения v (x), которые попадают в область определения функции y = f (v).
3. определить промежутки монотонности внешней функции y = f(v).
5. по графику внешней функции y = f (v) найти характер изменения функции y.
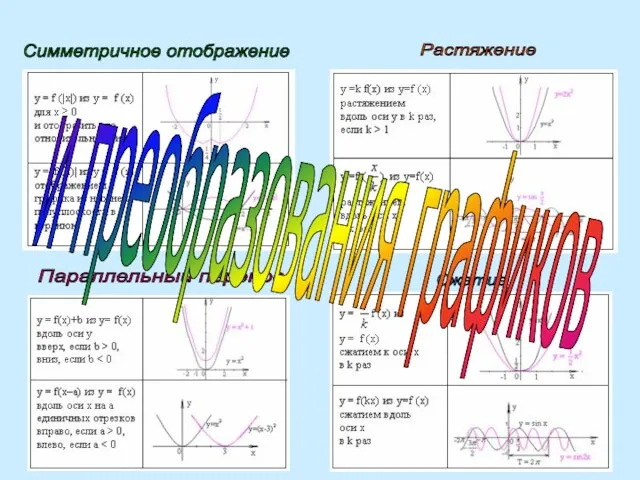
Алгоритм
построения
графиков сложных функций
И ВЫРАБОТАЛ
АЛГОРИТМ

0
0
1
3
1
-1
1
1/2
2
3
2
-1
x
1
Y= 2v
y
y
1/2
v
, где х=1, х=3
0
x
1
2
3
1
u
0
v
U=x2-4x+3
-1
x
V=1/(x2-4x+3)
1
2
3