Содержание
- 2. В данной презентации представлены основные правила по математике для учащихся начальных классов. Надеемся, что изучение математики
- 3. В путь....
- 4. 0 1 2 3 4 5 6 7 8 9 Это арабские цифры. Их всего десять.
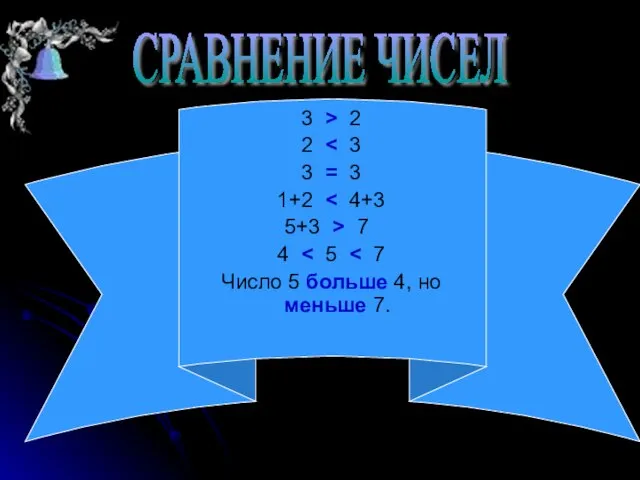
- 5. СРАВНЕНИЕ ЧИСЕЛ 3 > 2 2 3 = 3 1+2 5+3 > 7 4 Число 5
- 6. ЧИСЛА ЧЁТНЫЕ И НЕЧЁТНЫЕ Числа, которые делятся на 2, называются ЧЁТНЫМИ: 2 4 6 8 10…
- 7. СЛОЖЕНИЕ 5 + 2 = 7 первое второе сумма слагаемое слагаемое a + b = c
- 8. ПЕРЕСТАНОВКА СЛАГАЕМЫХ От перестановки слагаемых сумма не изменяется a + b = b + a Если
- 9. ВЫЧИТАНИЕ 5 - 3 = 2 уменьшаемое вычитаемое разность a – b = c Вычесть 1
- 10. СОСТАВ ЧИСЛА 2 = 1 + 1 3 = 1 + 2 = 1 + 1
- 11. СЛОЖЕНИЕ И ВЫЧИТАНИЕ чисел с переходом через десяток Одно из слагаемых надо разложить так, чтобы одна
- 12. ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ ПРИ РЕШЕНИИ ВЫРАЖЕНИЙ СО СКОБКАМИ Прибавить число к сумме, а также сумму к
- 13. Вычесть из суммы число можно несколькими способами (a + b) – c (a + b) –
- 14. ПРОВЕРКА СЛОЖЕНИЯ Сложение можно проверить вычитанием. Для этого надо из суммы вычесть одно слагаемое. Если в
- 15. ПРОВЕРКА ВЫЧИТАНИЯ Вычитание можно проверить сложением. Для этого надо к разности прибавить вычитаемое. Если в результате
- 16. УМНОЖЕНИЕ 2 • 3 = 6 первый второй произведение множитель множитель a • b = c
- 17. Если один из множителей равен 0, то произведение равно 0. a • 0 = 0 0
- 18. Умножение суммы на число (a + b) • c (a + b) • c = a
- 19. Проверка умножения - деление Если произведение двух чисел разделить на один из множителей, то получится другой
- 20. ДЕЛЕНИЕ : 3 = 2 делимое делитель частное a : b = c Если делитель равен
- 21. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ На 2 делятся числа, оканчивающиеся на чётную цифру: 28:2=14 174:2=87 На 3 делятся
- 22. ДЕЛЕНИЕ СУММЫ НА ЧИСЛО (a + b) : c (a + b) : c = a
- 23. ПРОВЕРКА ДЕЛЕНИЯ Если делимое разделить на частное, получится делитель а : b = c Проверка: а
- 24. ДЕЛЕНИЕ С ОСТАТКОМ Если делимое не делится на делитель, например 7 : 3, то надо подобрать
- 25. ЗАПОМНИ Увеличить число на несколько единиц – значит прибавить a + b Увеличить число в несколько
- 26. РЕШЕНИЕ УРАВНЕНИЙ Неизвестное число обозначается латинской буквой Х Х + а = с а – Х
- 27. ПЕРИМЕТР ФИГУРЫ Периметр – это сумма сторон геометрических фигур (квадрата, прямоугольника и т. д.), обозначается латинской
- 28. Площадь – это внутренняя часть фигуры (прямоугольника, квадрата и т. д.), обозначается латинской буквой S. Единицы
- 29. Конец
- 31. Скачать презентацию



























 Почтовая открытка 23 февраля
Почтовая открытка 23 февраля Изомерия. Классификация органических веществ.
Изомерия. Классификация органических веществ. Обыкновенные дроби (5 класс)
Обыкновенные дроби (5 класс) Проектно- исследовательская деятельность младших школьников
Проектно- исследовательская деятельность младших школьников Стили речи. Введение в стилистику
Стили речи. Введение в стилистику Конкурс как способ организации досугового мероприятия
Конкурс как способ организации досугового мероприятия 1. Oppitunti (2)
1. Oppitunti (2) Разработка рекламных мероприятий по продвижению компании «Горячие туры» в социальных сетях Дипломный проект Рябиги О.С Группа Р
Разработка рекламных мероприятий по продвижению компании «Горячие туры» в социальных сетях Дипломный проект Рябиги О.С Группа Р 20141105_voronezh_segodnya
20141105_voronezh_segodnya Экосистема. Структура экосистемы
Экосистема. Структура экосистемы Славяне в древности
Славяне в древности 29.11.2011г.Студенты группы Ф -22 совместно с кураторомпосетили
29.11.2011г.Студенты группы Ф -22 совместно с кураторомпосетили Презентация 3
Презентация 3 9 «В» Февраль 2012
9 «В» Февраль 2012 дата проведения: 11.01.10Провела:Учитель информатики и ВТХрусцелевская Н.В.Прослушал:5 класс
дата проведения: 11.01.10Провела:Учитель информатики и ВТХрусцелевская Н.В.Прослушал:5 класс Тема: «Великий художник природы – вода».
Тема: «Великий художник природы – вода». Vox – Технология будущего
Vox – Технология будущего Architecture Styles in America
Architecture Styles in America  План проведения педагогического совета 1. Вступление. Анализ выполнения решений предыдущего педагогического совета. 2. Доклад «Сти
План проведения педагогического совета 1. Вступление. Анализ выполнения решений предыдущего педагогического совета. 2. Доклад «Сти Загадочная смерть Маяковского
Загадочная смерть Маяковского Учебное исследование и проектная работа. Основные понятия
Учебное исследование и проектная работа. Основные понятия ЯПОНИЯ
ЯПОНИЯ Характеристика и особенности оформления справок, докладных и объяснительных записок
Характеристика и особенности оформления справок, докладных и объяснительных записок Религиозная толерантность
Религиозная толерантность Презентация на тему Динамика материальной точки. Работа и энергия
Презентация на тему Динамика материальной точки. Работа и энергия
 IT Construct ООО «Ай Ти Констракт»
IT Construct ООО «Ай Ти Констракт» РАЗРАБОТКА И ВНЕДРЕНИЕ УЧЕБНИКОВ ПО БАЙКАЛОВЕДЕНИЮ В ШКОЛЬНОЕ ОБРАЗОВАНИЕ БАЙКАЛЬСКОГО РЕГИОНА
РАЗРАБОТКА И ВНЕДРЕНИЕ УЧЕБНИКОВ ПО БАЙКАЛОВЕДЕНИЮ В ШКОЛЬНОЕ ОБРАЗОВАНИЕ БАЙКАЛЬСКОГО РЕГИОНА Верховный суд США
Верховный суд США