ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Содержание
Цель
Введение
Понятие правильного многогранника
Историческая справка
Тетраэдр
Гексаэдр
Октаэдр
Икосаэдр
Додекаэдр
Правильные многогранники в архитектуре и живописи
Звездчатые многогранники
Вывод

ЦЕЛЬ
Познакомиться с новым типом выпуклых многогранников-правильными многогранниками.

ВВЕДЕНИЕ
Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.
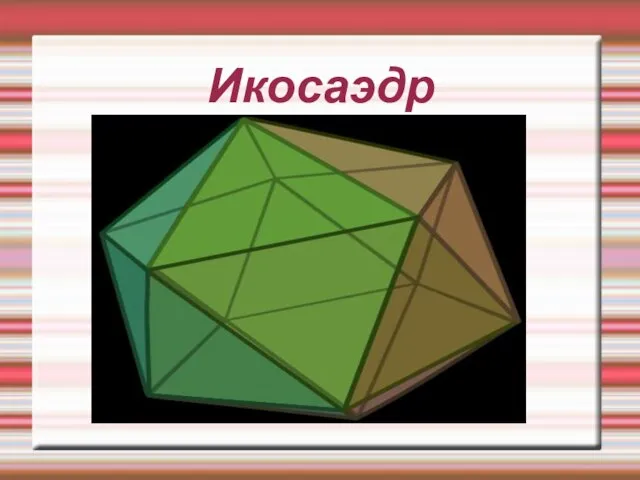
В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
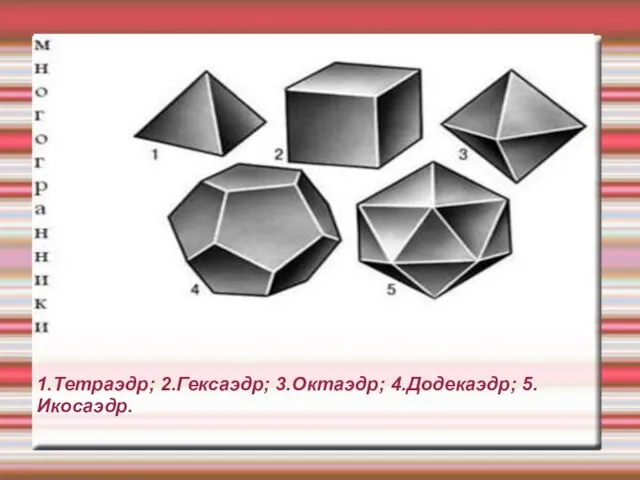
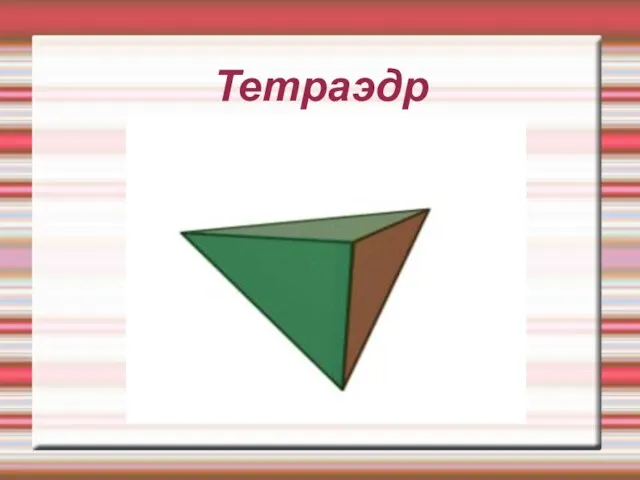
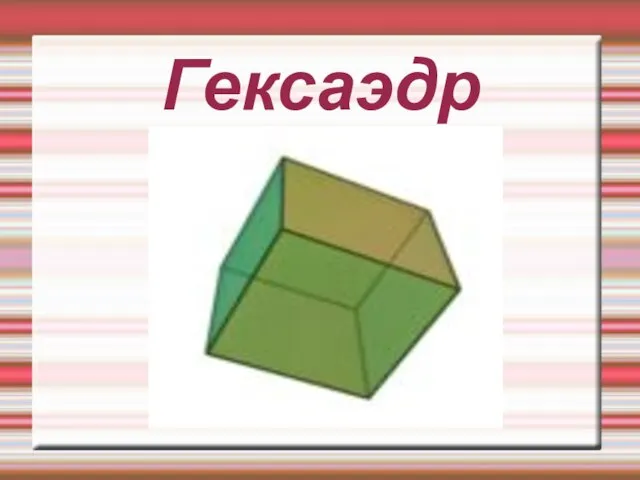
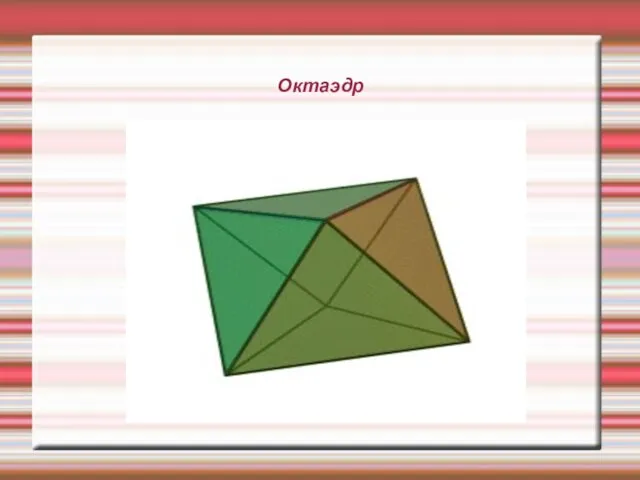
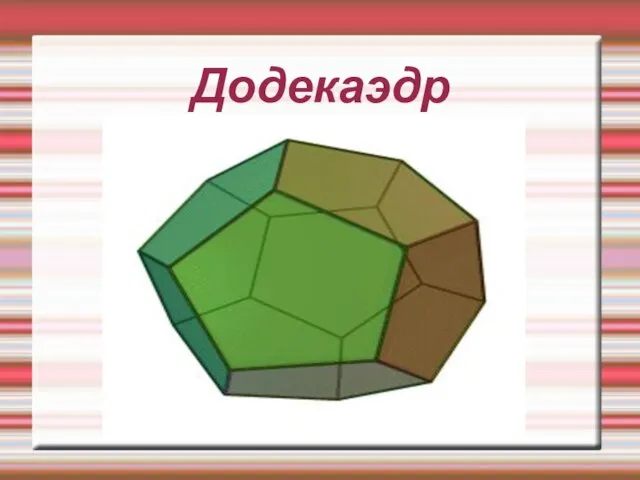
Правильные многогранники характерны для философии Платона, в честь которого и получили название «платоновы тела». Платон писал о них в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику. Земля сопоставлялась кубу, воздух — октаэдру, вода — икосаэдру, а огонь — тетраэдру. Для возникновения данных ассоциаций были следующие причины: жар огня ощущается чётко и остро (как маленькие тетраэдры); воздух состоит из октаэдров: его мельчайшие компоненты настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков (к которым ближе всего икосаэдры); в противоположность воде, совершенно непохожие на шар кубики составляют землю, что служит причиной тому, что земля рассыпается в руках, в противоположность плавному току воды. По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Аристотель добавил пятый элемент — эфир и постулировал, что небеса сделаны из этого элемента, но он не сопоставлял его платоновскому пятому элементу.

Понятие правильного многогранника
Правильный многогранник или платоново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией
Примеры: правильный гексаэдр(куб), правильный тетраэдр, правильный октаэдр, правильный икосаэдр, правильный додекаэдр

1.Тетраэдр; 2.Гексаэдр; 3.Октаэдр; 4.Додекаэдр; 5.Икосаэдр.

Тетраэдр

Определение:
Тетра́эдр (греч. τετραεδρον — четырёхгранник) — простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Свойства:
Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам.
Плоскость, проходящая через середины двух скрещивающихся рёбер тетраэдра, делит его на две равные по объёму части

Тетраэдры в микромире
Молекула метана СН4
Молекула аммиака NH3
Алмаз C — тетраэдр с ребром равным 2,5220 ангстрем
Флюорит CaF2, тетраэдр с ребром равным 3, 8626 ангстрем
Сфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем
Комплексные ионы [BF4] -, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+
Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO4]4

Тетраэдры в природе
Некоторые плоды, находясь вчетвером
на одной кисти, располагаются в вершинах
тетраэдра, близкого к правильному. Такая
конструкция обусловлена тем, что центры
четырёх одинаковых шаров, касающихся
друг друга, находятся в вершинах
правильного тетраэдра. Поэтому похожие
на шар плоды образуют подобное
взаимное расположение. Например,
таким образом могут располагаться
грецкие орехи.

Тетраэдры в технике
Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Граф четверичного триггера представляет собой тетраэдр.

Гексаэдр

Определение:
Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат.
Свойства:
Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям.
В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным, а его объём составляет 1/3 от объёма куба.
В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.

ИГРАЛЬНЫЕ КОСТИ

КУБИК РУБИКА

КУБИК СОМА

Октаэдр

Определение:
Окта́эдр (греч. οκτάεδρον, от греч. οκτώ, «восемь» и греч. έδρα — «основание») — один из пяти выпуклых правильных многогранников, так называемых Платоновых тел.
Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Свойства:
Октаэдр можно вписать в тетраэдр, притом четыре из восьми граней октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести ребер тетраэдра.
Октаэдр можно вписать в куб, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
В октаэдр можно вписать куб, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
Правильный октаэдр имеет симметрию Oh, совпадающую с симметрией куба.

Октаэдр

Октаэдр в природе

Икосаэдр

Определение:
Икоса́эдр (от др.-греч. εἴκοσι «двадцать»; ἕδρον «сидение», «основание») — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.
Свойства:
Икосаэдр можно вписать в куб, при этом шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба
В икосаэдр может быть вписан тетраэдр, так что четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра.
В икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра.
Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90.
Собрать модель икосаэдра можно при помощи 20 тетраэдров.

Додекаэдр

Определение:
Додека́эдр (от греч. δώδεκα — двенадцать и εδρον — грань) — двенадцатигранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.
Свойство:
В додекаэдр можно вписать куб так, что стороны куба будут диагоналями додекаэдра.

Правильные многогранники в архитектуре и живописи

Остров и маяк

Александровский маяк

Звездчатые многогранники
Правильные звёздчатые многогранники — это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники. Коши установил, что существует всего 4 правильных звёздчатых тела, не являющиеся соединениями платоновых и звёздчатых тел, называемые телами Кепплера — Пуансо: все 3 звёздчатых формы додекаэдра и одна из звёздчатых форм икосаэдра. Остальные правильные звёздчатые многогранники являются или соединениями платоновых тел, или соединениями тел Кепплера — Пуансо.

Живые многогранники

ВЫВОД
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон, и в каждой вершине многогранника сходится одно и то же число ребер.
Правильный тетраэдр (четырехгранник) — многогранник, составленный из четырех правильных треугольников.
Правильный гексаэдр (шестигранник) или куб — многогранник, составленный из шести правильных четырехугольников (квадратов).
Правильный октаэдр (восьмигранник) — многогранник, составленный из восьми правильных треугольников.
Правильный додекаэдр (двенадцатигранник) — многогранник, составленный из двенадцати правильных пятиугольников
Правильный икосаэдр (двадцатигранник) — многогранник, составленный из двадцати правильных треугольников.