Содержание
- 2. Содержание Немного истории Правильный многогранник Виды правильных многогранников Тетраэдр Куб Октаэдр Додекаэдр Икосаэдр Теорема Эйлера Табличные
- 3. Немного истории Хотелось бы сказать, что понятие правильных многогранников было введено древнегреческим философом Платоном и описано
- 4. Правильный многогранник Правильный многогранник – это выпуклый многогранник с максимально возможной симметрией.
- 5. Виды правильных многогранников Тетраэдр Куб Октаэдр Додекаэдр Икосаэдр
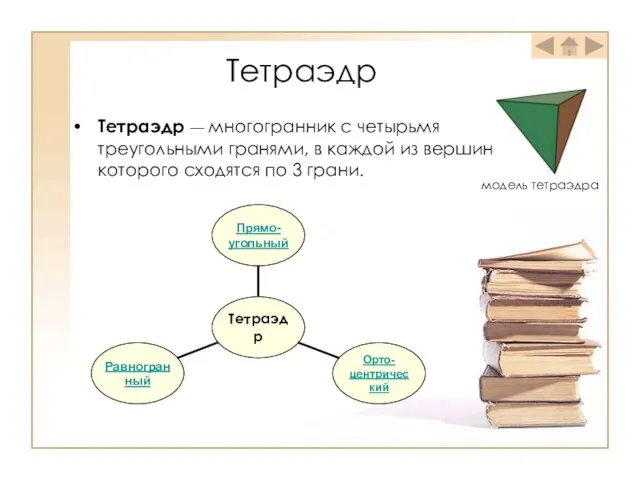
- 6. Тетраэдр Тетраэдр — многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3
- 7. Куб Куб или гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Модель куба
- 8. Октаэдр Октаэдр - правильный четырехугольный диэдр с равными ребрами, ограниченный восемью правильными треугольниками. Модель октаэдра
- 9. Додекаэдр Додекаэдр - правильный многогранник, составленный из двенадцати правильных пятиугольников. Модель додекаэдра
- 10. Икосаэдр Икосаэдр – правильный многогранник, каждая из 20 граней которого представляет собой равносторонний треугольник. Модель икосаэдра
- 11. Теорема Эйлера Формулы Эйлера: В-Р+Г=2, где В-число вершин, Р-число ребер, Г-число граней. В-Р+Г=Х, где Х=2,0,-4,-6… Невыпуклый
- 12. Табличные сведения
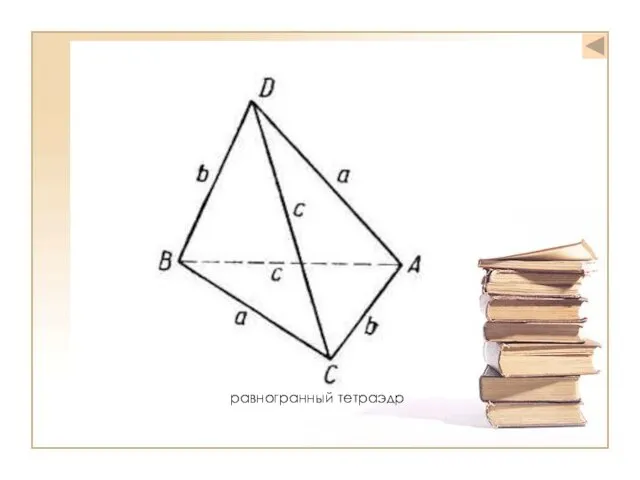
- 13. равногранный тетраэдр
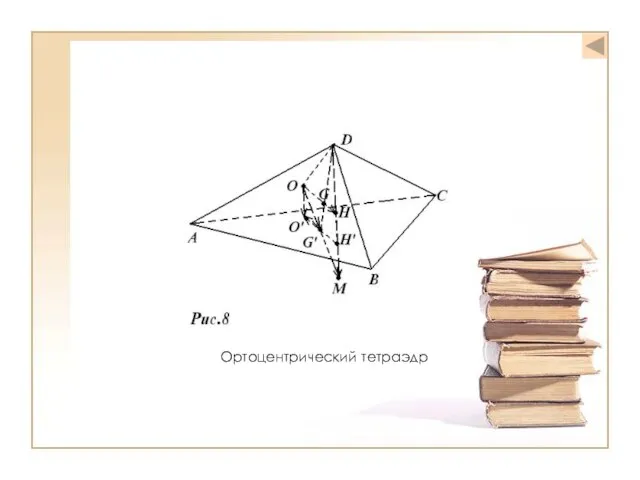
- 14. Ортоцентрический тетраэдр
- 16. Скачать презентацию










 Электромясорубка. Неисправность: сточились зубья передаточного колеса
Электромясорубка. Неисправность: сточились зубья передаточного колеса Животные красной книги
Животные красной книги Креативное медиапланированиеКак получить больше за те же деньги
Креативное медиапланированиеКак получить больше за те же деньги Введение в органическое сельское хозяйство
Введение в органическое сельское хозяйство Русская изба (урок ИЗО)
Русская изба (урок ИЗО) Подготовка к зачету. Беседы об искусстве
Подготовка к зачету. Беседы об искусстве Информационные ресурсы, создание их архивных копий и передача на государственное хранение
Информационные ресурсы, создание их архивных копий и передача на государственное хранение Онтология
Онтология Коммерческое право
Коммерческое право Папа, мама, я – дружная, здоровая, спортивная семья! 2008 год
Папа, мама, я – дружная, здоровая, спортивная семья! 2008 год крассная книга
крассная книга Системы, сети и устройства телекоммуникаций
Системы, сети и устройства телекоммуникаций Российское Движение Школьников
Российское Движение Школьников Відкритий доступ
Відкритий доступ Агрессивная визуальная среда
Агрессивная визуальная среда Семья – как малая группа
Семья – как малая группа Обучение педагогических кадров методам применения ИКТ на базе ММЦ ИКТ
Обучение педагогических кадров методам применения ИКТ на базе ММЦ ИКТ Трехмерная графика
Трехмерная графика Калибраторы. Назначение калибратора
Калибраторы. Назначение калибратора Учитель русского языка и литературы МОУ Яманской средней общеобразовательной школы Крутинского муниципального района Омской о
Учитель русского языка и литературы МОУ Яманской средней общеобразовательной школы Крутинского муниципального района Омской о Продукция Salus. Умная автоматика для дома
Продукция Salus. Умная автоматика для дома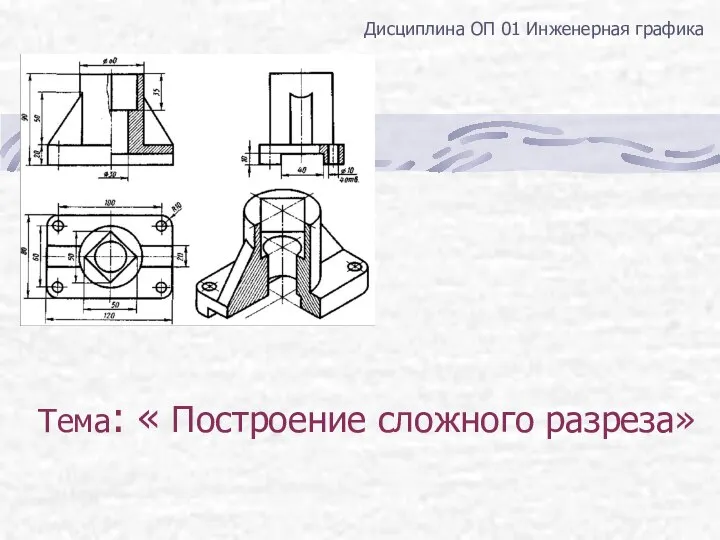 Построение сложного разреза на чертежах
Построение сложного разреза на чертежах Электронный журнал и дневник как условие активизации внутришкольного и внешнего контроля за системой оценки качества образовани
Электронный журнал и дневник как условие активизации внутришкольного и внешнего контроля за системой оценки качества образовани Презентация на тему Искусство Индии
Презентация на тему Искусство Индии ПМК Буревестник
ПМК Буревестник Bel VPN как средство надежной защиты комплексных информационных систем
Bel VPN как средство надежной защиты комплексных информационных систем Самопрезентация Тараскина Владислава
Самопрезентация Тараскина Владислава