Слайд 2Правильные многогранники
Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти

на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.
В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Театету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
Правильные многогранники характерны для философии Платона, в честь которого и получили название «Платоновы тела». Платон писал о них в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику. Земля сопоставлялась кубу, воздух — октаэдру, вода — икосаэдру, а огонь — тетраэдру. По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца».
Слайд 3Понятие правильного многогранника
Правильным называется выпуклый многогранник , у которого все грани-равные правильные
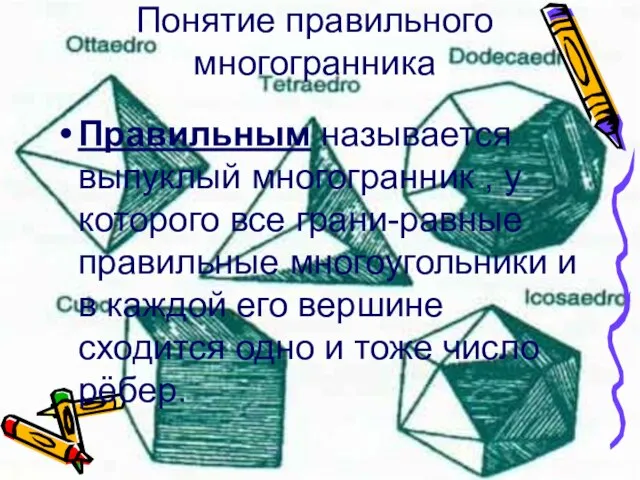
многоугольники и в каждой его вершине сходится одно и тоже число рёбер.
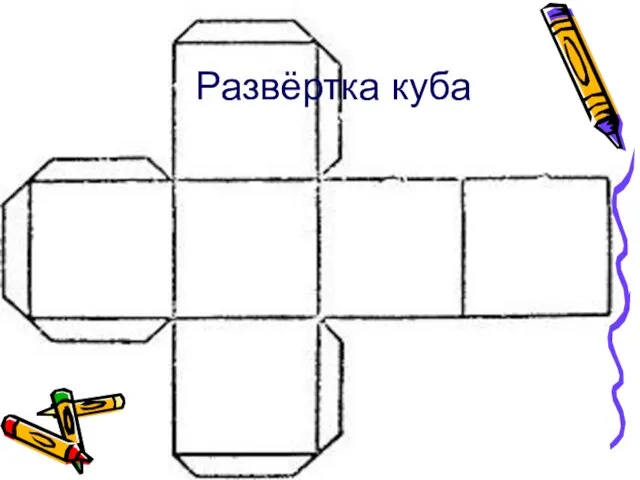
Слайд 4Куб
Правильный многогранник, каждая грань которого представляет собой квадрат. Каждая вершина куба является

вершиной трёх квадратов. Следовательно сумма плоских углов при каждой вершине равна 324
Слайд 5Куб
Имеет один центр симметрии -точку пересечения его диагоналей.
Куб имеет девять осей

симметрии.
Имеет девять плоскостей симметрии.
Слайд 6Свойства куба:
Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр
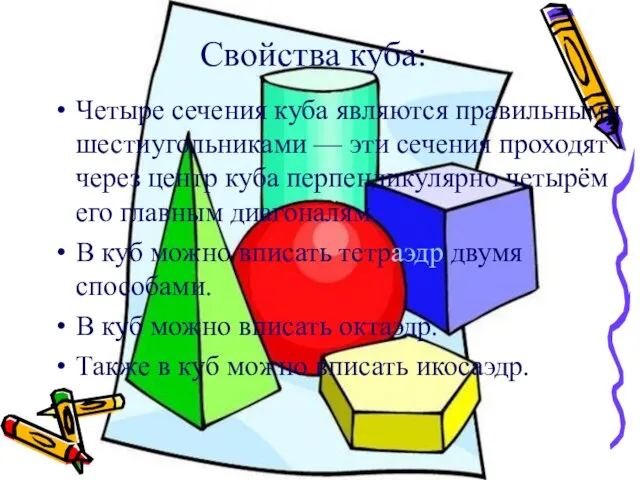
куба перпендикулярно четырём его главным диагоналям.
В куб можно вписать тетраэдр двумя способами.
В куб можно вписать октаэдр.
Также в куб можно вписать икосаэдр.
Слайд 7В форме куба кристаллизуется поваренная соль, флюорит и другие вещества.

Слайд 8Форму куба имеют игральные кости

Слайд 10«Кубик Рубика»
«Кубик Рубика» (разговорный вариант Кубик-Рубик). Первоначально был известен как «Магический кубик»,

изобретённый в 1974 году венгерским скульптором и преподавателем архитектуры Эрнё Рубиком.
Слайд 11Кубики сома
Кубики сома (англ. Soma cube) — это головоломка, являющаяся по сути трёхмерным аналогом

китайской головоломки пентамино.
Набор состоит из 7 фигур: из них одна фигура состоит из трёх кубиков, а остальные из четырёх кубиков. Из фигур нужно сложить кубик 3х3х3.
Слайд 12Кубики льда имеют красивую геометрическую форму.

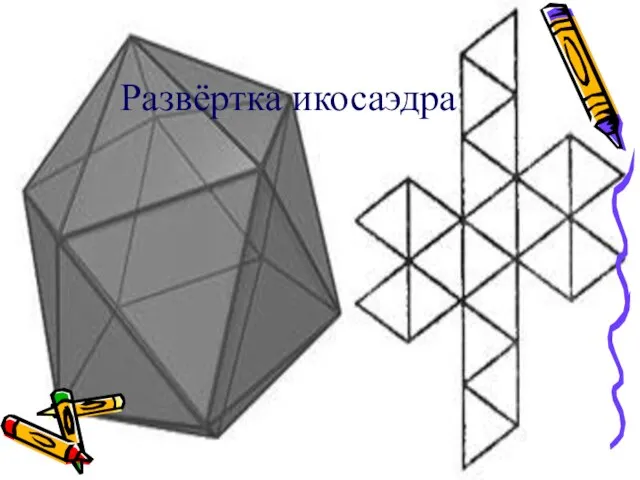
Слайд 14Правильный икосаэдр
Икоса́эдр (от греч. — двадцать; грань, лицо, основание) — правильный выпуклый многогранник,
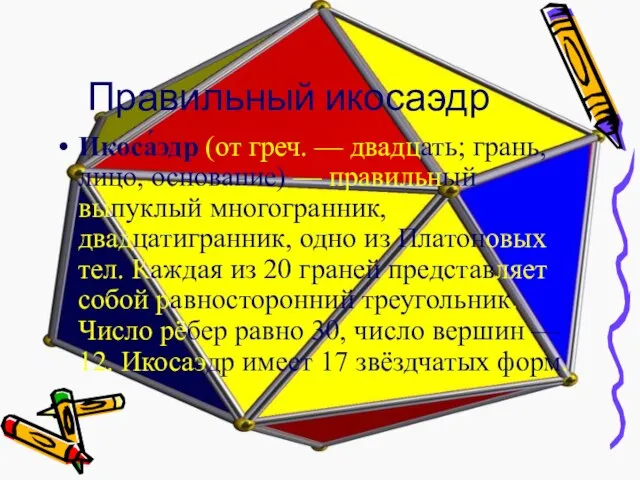
двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число рёбер равно 30, число вершин — 12. Икосаэдр имеет 17 звёздчатых форм.
Слайд 15Свойства икосаэдра:
В икосаэдр можно вписать куб.
В икосаэдр может быть вписан тетраэдр.
Также в
икосаэдр может быть вписан додекаэдр.
Форму правильного икосаэдра имеют внешние оболочки многих вирусов.













 Презентация на тему Тела и вещества Урок по окружающему миру 2 класс
Презентация на тему Тела и вещества Урок по окружающему миру 2 класс  Фенолформальдегидная смола
Фенолформальдегидная смола День Матери
День Матери Смотр-конкурс«Лучшая подготовительная группа детского сада по плаванию»
Смотр-конкурс«Лучшая подготовительная группа детского сада по плаванию» 20140108_formiruyushchee_otsenivanie
20140108_formiruyushchee_otsenivanie Правовые основы противодействия коррупции. Лекция 2
Правовые основы противодействия коррупции. Лекция 2 Презентация на тему Тундра и лесотундра России
Презентация на тему Тундра и лесотундра России История письменности на Руси
История письменности на Руси лекция 1. Введение в УЧР
лекция 1. Введение в УЧР Зима 2009/2010:пробный шар
Зима 2009/2010:пробный шар Типы конденсаторов. Применение конденсаторов
Типы конденсаторов. Применение конденсаторов Строим пирамиду
Строим пирамиду Мамин платок
Мамин платок Воспитательная система «Школьные годы чудесные» Классный руководитель: Яна Станиславовна Галеева.
Воспитательная система «Школьные годы чудесные» Классный руководитель: Яна Станиславовна Галеева. Формирование этнической толерантности как нравственного аспекта на уроках географии
Формирование этнической толерантности как нравственного аспекта на уроках географии Презентация на тему Хлеб – всему голова
Презентация на тему Хлеб – всему голова  Фритьоф Нансен – полярный исследователь и учёный.
Фритьоф Нансен – полярный исследователь и учёный. RUS-01 Compensation plan Wantage One 2.4 Euro
RUS-01 Compensation plan Wantage One 2.4 Euro Фелтинг
Фелтинг Материалы по гигиене и санитарии
Материалы по гигиене и санитарии Проектирование электрооборудования автономных объектов
Проектирование электрооборудования автономных объектов Подготовительная группа «Солнышко»
Подготовительная группа «Солнышко» Система нравственного воспитания через курс «Этическая грамматика»
Система нравственного воспитания через курс «Этическая грамматика» Презентация на тему Первые печатные книги на Руси
Презентация на тему Первые печатные книги на Руси  Кислоты
Кислоты Продажа недвижимого имущества
Продажа недвижимого имущества Т
Т Определение емкости рынка товаров народного потребления (на примере Красноярского края)
Определение емкости рынка товаров народного потребления (на примере Красноярского края)