Правильные выпуклые многогранники

«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук»
Л. Кэрролл

Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют многогранной поверхностью или многогранником.

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.

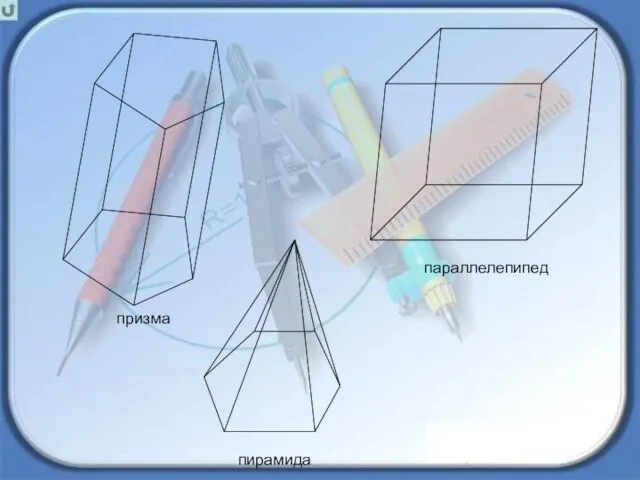
призма
параллелепипед
пирамида

Все ребра правильного многогранника равны друг другу.
Все двугранные углы правильного многогранника, содержащие две грани с общим ребром равны.

Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники при n≥6.
Каждая вершина правильного многогранника может быть вершиной либо трех, четырех или пяти равносторонних треугольников, либо трех квадратов, либо трех правильных пятиугольников.

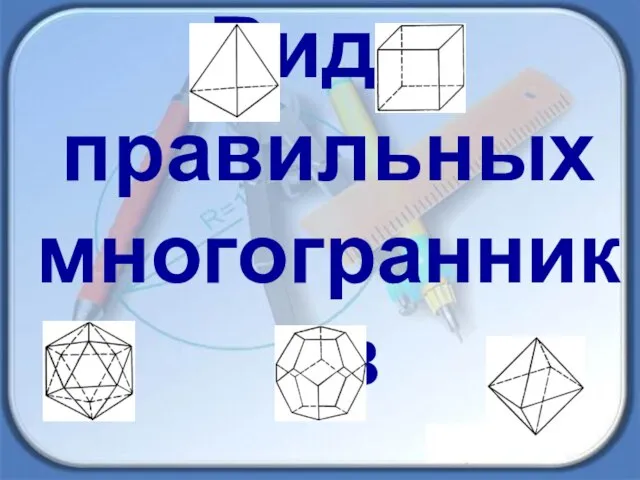
Виды правильных многогранников

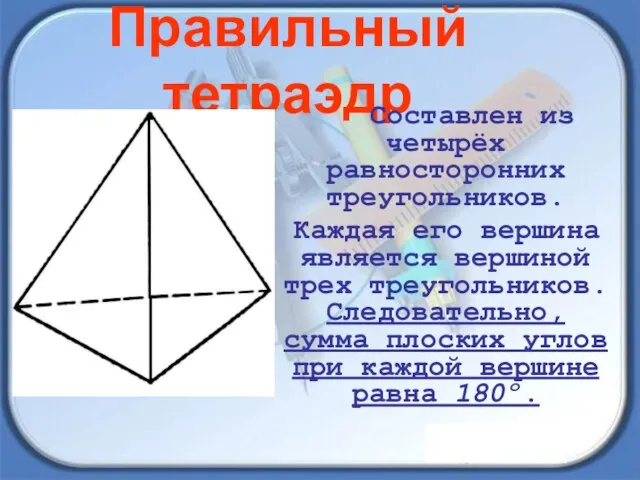
Правильный тетраэдр
Составлен из четырёх равносторонних треугольников.
Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180º.

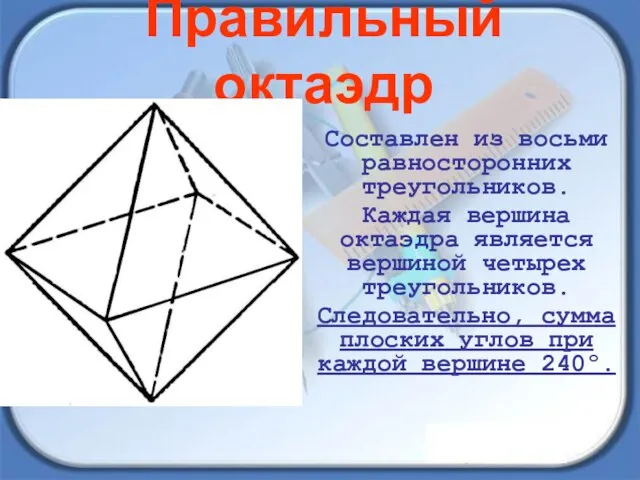
Составлен из восьми равносторонних треугольников.
Каждая вершина октаэдра является вершиной четырех треугольников.
Следовательно, сумма плоских углов при каждой вершине 240º.
Правильный октаэдр

Правильный икосаэдр
Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников.
Следовательно, сумма плоских углов при каждой вершине равна 300º.

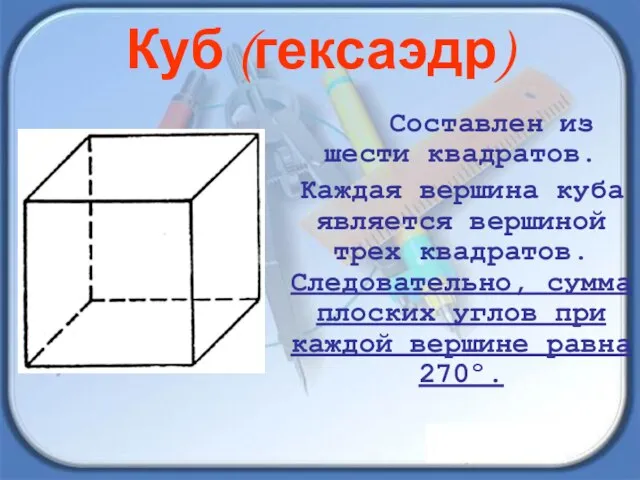
Составлен из шести квадратов.
Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270º.
Куб (гексаэдр)

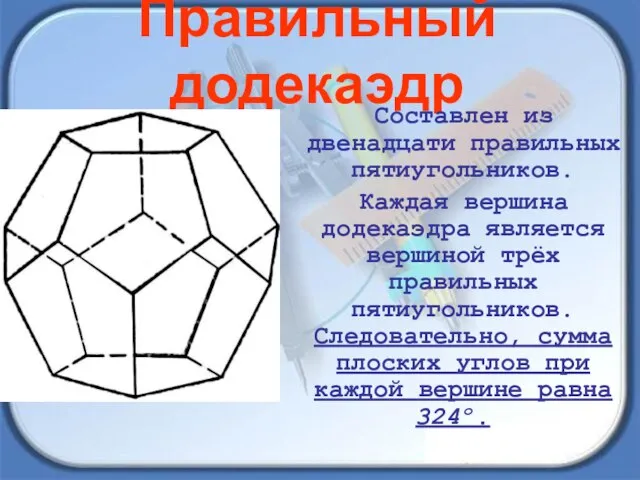
Правильный додекаэдр
Составлен из двенадцати правильных пятиугольников.
Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324º.

пришли из Древней Греции,
в них указывается число граней:
«эдра» − грань;
«тетра» − 4;
«гекса» − 6;
«окта» − 8;
«икоса» − 20;
«додека» − 12.
Названия многогранников

Правильные многогранники иногда называют Платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном
(ок. 428 – ок. 348 до н.э.).
Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.

Идеи Платона и Кеплера о связи правильных многогранников с гармоничным устройством мира и в наше время нашли своё продолжение в интересной научной гипотезе, которую в начале 80-х гг. высказали московские инженеры В. Макаров и В. Морозов.
Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли . Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.
Икосаэдро-
додекаэдровая
структура Земли
Икосаэдро-додекаэдровая структура Земли

Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки; 62 вершины и середины рёбер многогранников, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления.
Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник.
Дальнейшие исследования Земли, возможно, определят отношение к этой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.

Большой интерес к формам правильных многогранников проявляли также скульпторы, архитекторы, художники. Их всех поражало совершенство, гармония многогранников.
Леонардо да Винчи (1452 – 1519) увлекался теорией многогранников и часто изображал их на своих полотнах.
Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со своими учениками на фоне огромного прозрачного додекаэдра.

«Тайная вечеря» Леонардо Да Винчи

«Тайная вечеря» Сальвадор Дали

«Правильные многогранники и природа»

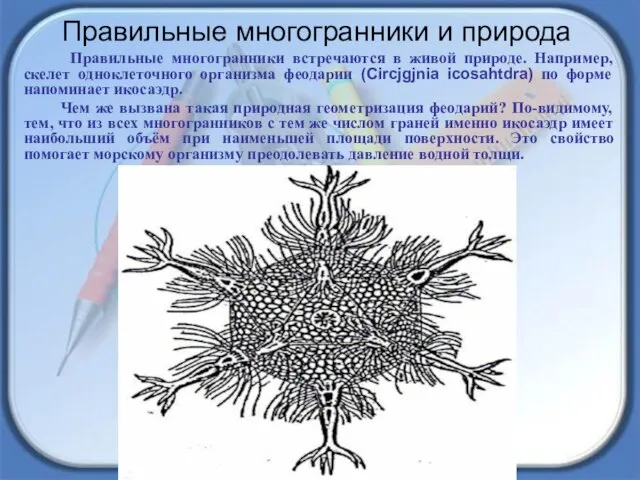
Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр.
Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Правильные многогранники и природа

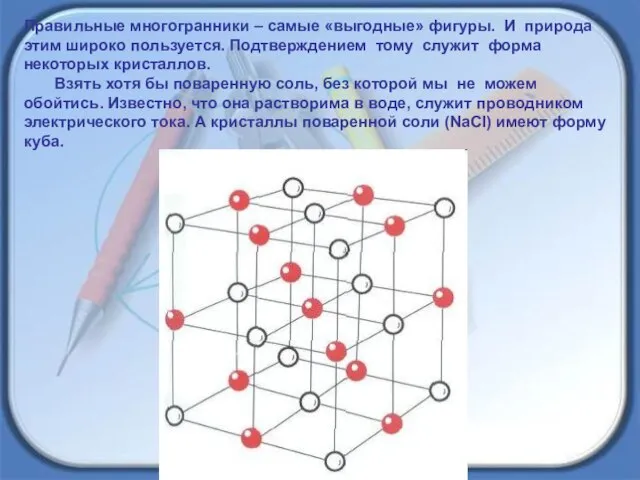
Правильные многогранники – самые «выгодные» фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов.
Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба.

Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра.