Предельные возможности макроуправляемых систем

Типовые задачи
Термодинамика.
Максимум извлеченной работы.
Предельная средняя мощность.
Минимальная работа разделения.
Распределение температур, концентраций, энергии в открытых системах.
Микроэкономика.
Максимум извлеченного капитала.
Предельная интенсивность прибыли.
Минимальные затраты на разделение систем.
Распределение ресурсов в открытых системах.

Методология
Термодинамика.
Уравнения ТД балансов (материальный, энергетический, энтропийный).
Микроэкономика.
Уравнения экономических балансов (ресурс, капитал, фактор необратимости).
Расчет минимальной диссипации энергии (капитала).
Построение области реализуемости системы.

Некоторые результаты
1. Процессы минимальной диссипации:
Термодинамика:
(1)
J – поток, X – движущая сила.
Микроэкономика:
(2)
J – поток ресурса, p – оценка, c – цена, M, N – запасы капитала и ресурса.

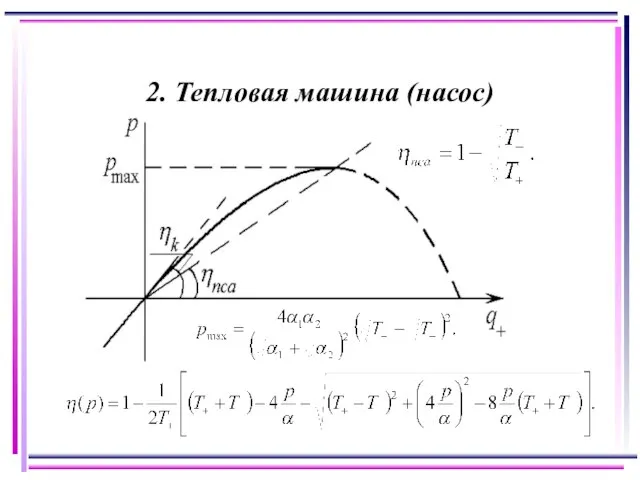
2. Тепловая машина (насос)

3. Максимальная интенсивность извлечения прибыли посредником

4. Функция благосостояния S(N,M) существует
оценка капитала
оценка i-го ресурса
аналог соотношений Максвелла

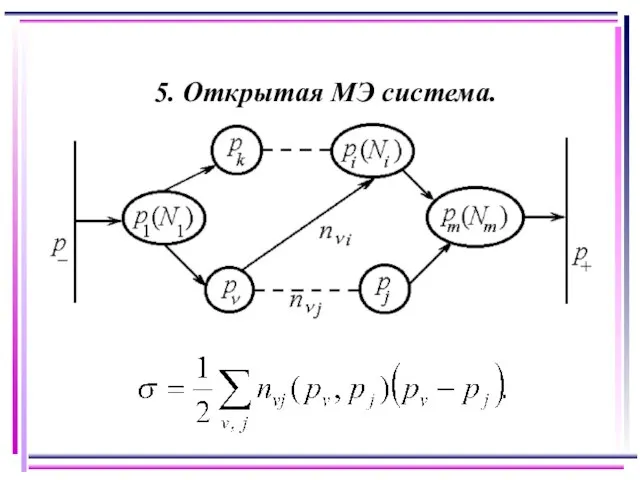
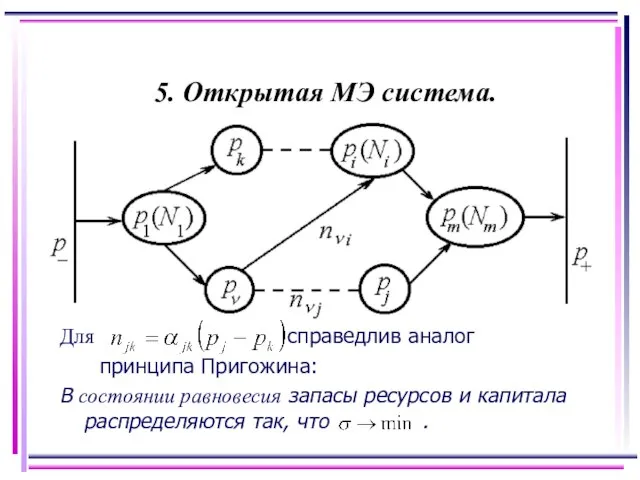
5. Открытая МЭ система.

Для справедлив аналог
принципа Пригожина:
В состоянии равновесия запасы ресурсов и капитала распределяются так, что .
5. Открытая МЭ система.

Минимальная работа разделения N молей смеси
Обратимая
Необратимая
xi – начальные концентрации.
Выбор последовательности разделения.
6. Процессы разделения.

Основные публикации
Розоноэр Л.И., Цирлин А.М. Оптимальное управление термодинамическими системами. АиТ, \No 1-3, 1983.
Tsirlin A.M., Boeme C. Dynamische Grundoperationen der Verfahrenstechnik-Modellirung und optimale Steurung. Berlin. Akademie Verlag. 1984
Цирлин А.М. Оптимальные циклы и циклические pежимы. М., Энеpгоатом-издат, 1985.
Цирлин А.М., Крылов Ю.М., Миронова В.А. Сегpегиpованные пpоцессы в химической пpомышленности. М., Химия, 1986.
Малых В.Л. Термодинамические ограничения и эффективность изотермических процессов разделения. Деп. ВИНИТИ № 2020-В87.1987.с.12.
Mironowa V.A., Tsirlin A.M., Kazakow V.A., Berry R.S. Finite-time thermodynamics: exergy and optimization of finite-constrained processes J.Appl.Phys. 76(2) 1994.
Tsirlin A.M., Kazakow V.A., Berry R.S. Finite-time thermodynamics: Limiting performance of rectification and minimal entropy production in mass transfer. J.of Phys.Chem.,98,3330-3336,1994.
Циpлин А.М., Оптимальное упpавление обменом pесуpсами в экономических системах. Автоматика и телемеханика,1995 N 3, с. 116-126.
Tsirlin A.M. Methods of duality in problems about expendiency of usage and optimization of cyclic regimes of technological processes. 4th IFAC Symposium on dynamics and control of chemical reactors, distillation columns and batch processes. Copenhagen 1995.

1997
Цирлин А.М. Методы усредненной оптимизации и их приложения. М. Физмат-лит.,1997.с.304.
Цирлин А.М., Миронова В.А., Амелькин С.А. Процессы минимальной диссипации. Теоретические основы химической технологии 1997.№6, с.649-658.
Соболев В.А., Миронова В.А. Цирлин А.М., Оптимальное управление потоками сырья и готовой продукции за счет выбора цен. Автоматика и телемеханика. №4, 1997
1998
Амелькин С.А., Андресен Б., Саламон П., Цирлин А.М. Предельные возможности тепломеханических систем с одним источником. Изв. РАН. сер. Энергетика №2.1998.с.118-126
Беляева Н.А., Цирлин А.М. Оптимальное управление покупкой и продажей ценных бумаг. Автоматика и телемеханика. № ,1998.с.135-143.
Tsirlin A. M., Kazakov V. A. Finite-time thermodynamics: active potentiostatting, J. of Physics D, 31. p.2264-2268 (1998).
Tsirlin A.M., Mironova W.A,, Amelkin S.A., Kazakov V.A. Finite-time thermodynamics: Conditions of minimal dissipation for thermodynamic processes with given rate, Phys.Rev. E, 58, (1998)
Цирлин А.М., Беляева Н.П. О связи продолжительности и диссипации для процессов теплообмена. Теплоэнергетика. 1998, №9 с53-56.

1999
Berry R.S., Kazakov V, Sieniutycz S., Szwast Z., Tsirlin A.M. Termodynamic Optimization of Finite-Time Processes. John Wiley & Sons, LTD, 1999
Цирлин А.М. Второй закон термодинамики и предельные возможности тепловых машин. Журнал технической физики. №1,1999.с.140-142.
Амелькин С.А. ,Андресен Б., Саламон П. Цирлин А.М. Предельные возможности тепломеханичес-ких систем с несколькими источниками. Изв.РАН, сер.Энергетика, №1,1999,с. 165-172.
Цирлин А.М., Андресен Б., Хоффман K.X. Использование методов термодинамики конечного времени при проектировании экологически безопасных производств. Программные системы: Теоретические основы и приложения. М. Наука. Физматлит.1999. с.72-78.
Амелькин С.А., Осипова Н.В. Предельные возможности тепло- и массообменных систем в зависимости от гидродинамики потоков. Программные системы: Теоретические основы и приложения. М. Наука. Физматлит.1999. с.88-96.
Цирлин А.М., Колинько Н.А., Задача извлечения максимальной прибыли в системах ресурсообмена. Труды международной конференции по интеллектуальному управлению. Наука. Физматлит , 1999.
Tsirlin A.M., Kazakov V.A. Limiting possibilities of regenerative systems. Recent Advances in Finite-Time Thermodynamics. C.Wu, L.Chen (eds) Nova Science Publishing, 1999.

2000
Миронова В.А., Амелькин С.А., Цирлин А.М. Математические методы термодинамики при конечном времени. М. Химия. 2000
Цирлин А.М. Оптимизация деятельности посредника в условиях задержки поставок и платежей. Автоматика и телемеханика, № 3. 2000.
Миронова В.А., Соболев В.А., Цирлин А.М., Усредненные задачи нелинейного программирования при оптимальном управлении ценами и товарными потоками на производстве. Автоматика и Телемеханика №7, стр. 131-139. 2000.
Tsirlin A.M., Kazakov V. A., Maximal work problem in finite-time thermodynamics. Phys. rev. E , V, 62. N1 p. 307-316 (2000).
Цирлин А. М. Условия оптимальности усредненных задач с нестационарными параметрами. ДАН, 2000, т.374,№2, с.174-177.

2001
Цирлин А.М. Оптимальные процессы и управление в необратимой микроэкономике. Автоматика и телемеханика, № 5, стр.159-170, 2001.
Tsirlin A., Amelkin S., Dissipation and Conditions of Equilibrium for Open Microeconomic System. Open Sys. & Information Dyn. 8: 157-168, 2001.
Amelkin S., Tsirlin A., Optimal Choice of Prices and Flows in a Complex Open Industrial System. Open Sys. & Information Dyn. 8: 169-181, 2001
Амелькин С.А., Бурцлер Й.М., Хоффман К.Х., Цирлин А.М. Оценка предельных возможностей процессов разделения. Теорет.осн. хим. технологии. Т.35, № 3. С.232-238, 2001 г
Андреев Д.А., Могутов В.А., Цирлин А.М. Выбор расположения слоев ограждающей конструкции с учетом предотвращения внутренней конденсации Строительные Материалы, № 12, с.42-45, 2001.
Цирлин А.М., Казаков В.А. Область реализуемости термодинамических систем заданной производительности. Известия РАН, Энергетика, № 5, стр.44-51, 2001.
Tsirlin A.M., Kazakov V., Kolinko N.A. Irreversibility and Limiting Possibilities of Macrocontrolled Systems: 1. Thermodynamics. Open Sys.& Inform. Dyn. 8, №4, 315-328, 2001
Tsirlin A.M., Kazakov V., Kolinko N.A. Irreversibility and Limiting Possibilities of Macrocontrolled Systems: 2.Microeconomics, Open Sys.& Inform. Dyn. 8, № 4, 329-347, 2001

2002
Цирлин А.М. Оптимальные процессы в необратимой термодинамике и микроэкономике. М.: Физматлит. 2002.,416с.
Цирлин А.М., Амелькина М.А., Амелькин С.А. Модель производственной фирмы в открытой микроэкономической системе. Математическое моделирование. Т.14, №4, стр.21-34,2002.
Амелькин С.А. Динамическая модель поведения экономического агента в открытой микроэкономической системе. Обобщенные решения в задачах управления, Переславль-Залесский, 2002, с.155-159.
Амелькин С.А., Мартинаш К., Цирлин А.М. Задачи оптимального управления необратимыми процессами в термодинамике и микроэкономике.(обзор).Автоматика и телемеханика, №4, 2002. С. 3-25.
Amelkin S.A., Hoffmann K.H., Tsirlin A.M., Sicre B. Limiting performance of heat exchangers taking into account hydrodynamic characteristics of the flows. Periodica Politechnica, No. 8, 2002.
Колинько Н.А. Цирлин А.М. Оптимальные процессы в необратимой термодинамике и микроэкономике. Теория и системы управления, №6, 2002.
Колинько Н.А., Цирлин А.М., Классификация объектов управления по типу оптимальных процессов. Автоматика и телемеханика, 2002 (в печати).
Tsirlin A.M., Kazakov V., Zubov D.V. Finite-Time Thermodynamics: Limiting Possibilities of Irreversible Separation Processes. J.Phys.Chem. 106 (9), 2002.

Проблема эквивалентности дифференциальных уравнений

Постановка задач
Для широких классов дифференциальных уравнений найти необходимые и достаточные условия существования замены переменных, приводящее одно уравнение к другому.
Условия формулируются в терминах дифференциальных инвариантов этих уравнений, т.е. величин, не меняющихся при заменах переменных.
Разработка алгоритмов вычисления дифференциальных инвариантов является основным содержанием этого направления.

Методы
Современные дифференциально-геометрические методы (Геометрия дифференциальных уравнений и симметрий) и компьютерно-алгебраические средства (REDUCE, MAPLE).

Некоторые результаты
Получена локальная классификация линейных обыкновенных дифференциальных уравнений с точностью до замен переменных.
Для нелинейных обыкновенных дифференциальных уравнений 2-го порядка получен дифференциальный инвариант, отвечающий за возможность приведения уравнений к линейному виду заменами переменных.
Для нелинейных обыкновенных дифференциальных уравнений 3-го порядка получены явные условия на правую часть уравнения, необходимые и достаточные для существования замены переменных, приводящее уравнение к простейшему виду.

Основные публикации
В.А.Юмагужин, Классификация линейных обыкновенных дифференциальных уравнений, II, Дифференциальные уравнения, 2002, Т. 39, Вып. 1, стр. 1 - 6.
В.А.Юмагужин, Классификация линейных обыкновенных дифференциальных уравнений, I, Дифференциальные уравнения, 2002, Т. 38, Вып. 6, стр. 1 - 8.
V.A.Yumaguzhin, Contact classification of linear ordinary differential equations. Acta Applicandae Mathematicae, Vol. 72, No. 1/2, June 2002, pp. 155-181.
В.А.Юмагужин, Локальная классификация линейных обыкновенных дифференциальных уравнений, 2001, ДАН, Т. 377, No 5, стр. 605 - 607.
V.N.Gusyatnikova, V.A.Yumaguzhin, Contact transformations and local reducibility of ODEs to the form y'''=0,
Acta Applicandae Mathematicae, 1999, Vol. 56, No. 3, pp. 155 - 179.
V.A.Yumaguzhin, Point transformations and classification of 3-order linear ODEs,
Russian Journal of Mathematical Physics, 1996, Vol. 4, No. 3, pp. 403 - 410.
V.A.Yumaguzhin, Classification of 3-rd order linear ODEs up to equivalence,
Journal of Differential Geometry and its Applications, 1996, Vol. 6, No. 4, pp. 343 - 350.
В.Н.Гусятникова, В.А.Юмагужин, Точечные преобразования и линеаризуемость обыкновенных дифференциальных уравнений 2-го порядка,
Математические заметки, 1991, Т. 49, Вып. 1, стр. 146 - 148.

Геометрические условия разрешимости уравнений свертки

Основное направление работы
Исследование геометрических свойств множеств на плоскости, обеспечивающих разрешимость линейных дифференциальных операторов бесконечного порядка с постоянными коэффициентами в пространстве аналитических функций.

Результаты
Получен критерий разрешимости уравнений свертки с произвольной правой частью.
Исследованы взаимосвязи различных определений выпуклости плоского множества в заданных направлениях.
Установлены свойства выпуклости в направлении, связывающие это понятие с обычной выпуклостью и другими родственными понятиями.