Содержание
- 3. Стереометрия- это раздел геометрии, в котором изучаются свойства фигур в пространстве.
- 4. Геометрия возникла из практических нужд человека
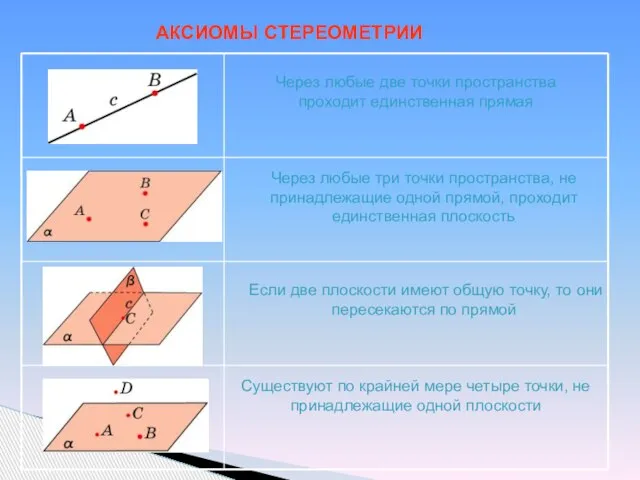
- 5. АКСИОМЫ СТЕРЕОМЕТРИИ Через любые две точки пространства проходит единственная прямая Через любые три точки пространства, не
- 6. ВОПРОС 1 Сколько прямых проходит через две точки пространства? Ответ: Одна.
- 7. ВОПРОС 2 Сколько плоскостей проходит через три точки пространства? Ответ: Одна, если три точки не принадлежат
- 8. ВОПРОС 3 Сколько общих точек могут иметь две плоскости? Ответ: Ни одной, или бесконечно много.
- 9. ВОПРОС 4 Верно ли утверждение, что всякие: а) три точки; б) четыре точки пространства принадлежат одной
- 10. ВОПРОС 5 Верно ли, что если окружность имеет с плоскостью две общие точки, то окружность лежит
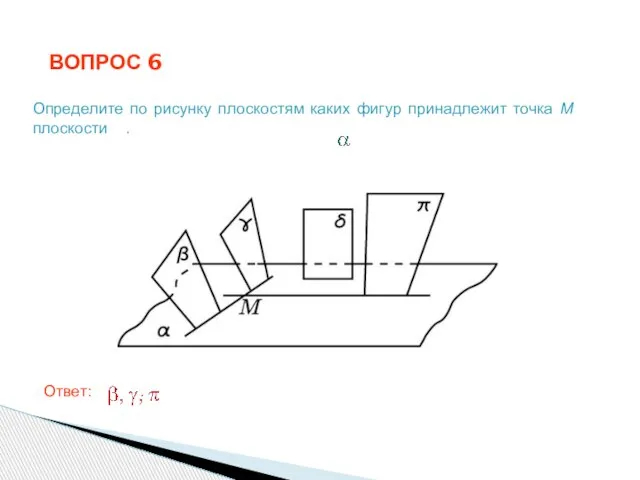
- 11. ВОПРОС 6
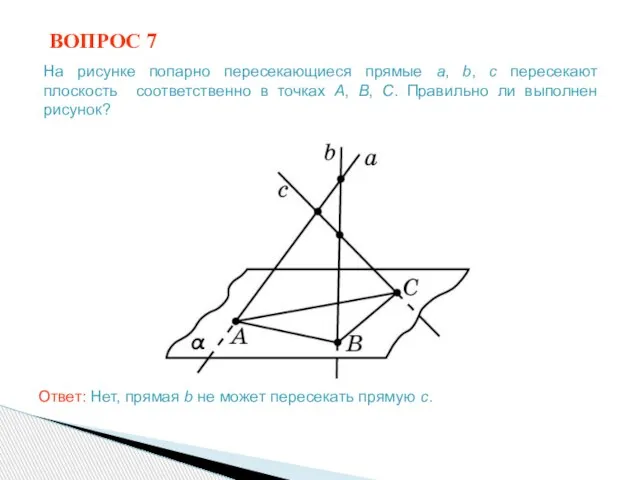
- 12. ВОПРОС 7 Ответ: Нет, прямая b не может пересекать прямую c. На рисунке попарно пересекающиеся прямые
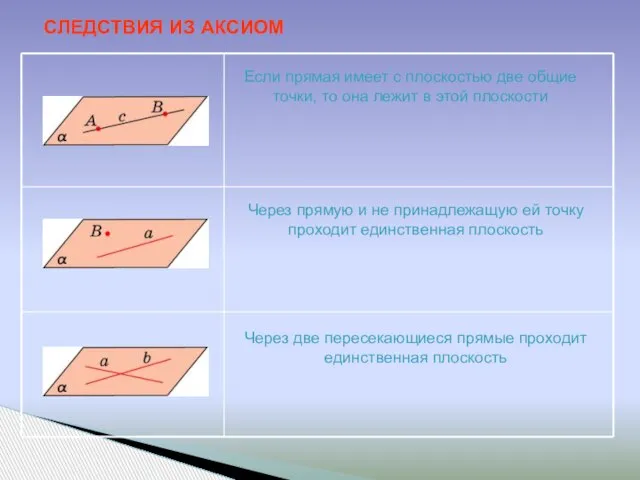
- 13. СЛЕДСТВИЯ ИЗ АКСИОМ Если прямая имеет с плоскостью две общие точки, то она лежит в этой
- 14. Упражнение 1 Четыре точки не принадлежат одной плоскости. Могут ли три из них принадлежать одной прямой?
- 15. Упражнение 2 Три вершины параллелограмма принадлежат некоторой плоскости. Верно ли утверждение о том, что и четвёртая
- 16. Упражнение 3 Две вершины и точка пересечения диагоналей параллелограмма принадлежат одной плоскости. Верно ли утверждение о
- 17. Упражнение 4 Могут ли вершины замкнутой ломаной, состоящей из трёх звеньев, не принадлежать одной плоскости? Ответ:
- 18. Упражнение 5 Могут ли вершины замкнутой ломаной, состоящей из четырёх звеньев, не принадлежать одной плоскости? Ответ:
- 19. Упражнение 6 Верно ли, что через любые две прямые проходит плоскость? Ответ: Нет.
- 20. Упражнение 7 Прямые a, b, c попарно пересекаются. Верно ли, что они лежат в одной плоскости?
- 21. Упражнение 8 Верно ли, что любая прямая, пересекающая каждую из двух данных пересекающихся прямых, лежит в
- 22. Упражнение 9 Прямые a и b пересекаются в точке C. Через прямую a проходит плоскость ,
- 23. Упражнение 10 Верно ли, что через любые две прямые проходит плоскость? Ответ: Нет.
- 24. Упражнение 11 Верно ли, что через три пересекающиеся прямые проходит плоскость? Ответ: Нет.
- 25. Упражнение 12 Сколько плоскостей можно провести через четыре точки? Ответ: Или одну, или ни одной.
- 26. Упражнение 13 Сколько плоскостей можно провести через различные тройки из пяти точек, никакие четыре из которых
- 27. Упражнение 14 На сколько частей делят пространство три плоскости, имеющие одну общую точку? Ответ: 8.
- 29. Скачать презентацию






















 Институциональное обеспечение стратегии развития муниципального образования
Институциональное обеспечение стратегии развития муниципального образования Традиционные украшения бурят
Традиционные украшения бурят Логика высказываний Алгоритм построения
Логика высказываний Алгоритм построения Всемирный день качества
Всемирный день качества РЕКЛАМНЫЕ ВОЗМОЖНОСТИ СЕТИ МАГАЗИНОВ МОЛОДЕЖНОЙ ОДЕЖДЫ ТВОЕ
РЕКЛАМНЫЕ ВОЗМОЖНОСТИ СЕТИ МАГАЗИНОВ МОЛОДЕЖНОЙ ОДЕЖДЫ ТВОЕ Имя существительное в русском и английском языках
Имя существительное в русском и английском языках Многофакторная модель интеллекта по Луису Терстоуну
Многофакторная модель интеллекта по Луису Терстоуну Избирательное право для всех и каждого
Избирательное право для всех и каждого Практическая работа по проектам Семейный клуб и Летние площадки психологической поддержки
Практическая работа по проектам Семейный клуб и Летние площадки психологической поддержки Британия, Британия, туманная страна…
Британия, Британия, туманная страна… Презентация на тему Виды международных договоров
Презентация на тему Виды международных договоров  MoBill – CAS(Control Access Service ) Учет использования услуг по магнитным картам
MoBill – CAS(Control Access Service ) Учет использования услуг по магнитным картам Номенклатура алканов разветвлённого строения
Номенклатура алканов разветвлённого строения Конституционно-правовой статус депутата Парламента Республики Казахстан. Тема 9
Конституционно-правовой статус депутата Парламента Республики Казахстан. Тема 9 Добро пожаловать!
Добро пожаловать! Предложения слушателей курсов ПК по результатам мониторинга Для совершенствования качества повышения квалификации слуша
Предложения слушателей курсов ПК по результатам мониторинга Для совершенствования качества повышения квалификации слуша Флора и фауна Мордовского края.
Флора и фауна Мордовского края. Концепция саморегулирования (Общие положения)
Концепция саморегулирования (Общие положения) Целеполагание в современных образовательных системах
Целеполагание в современных образовательных системах Методы и формы гражданского образования
Методы и формы гражданского образования Административное выдворение за пределы РФ. Дисквалификация
Административное выдворение за пределы РФ. Дисквалификация РУССКИЙ ЯЗЫК КАК ИНОСТРАННЫЙ Виртуальная выставка читального зала гуманитарных наук
РУССКИЙ ЯЗЫК КАК ИНОСТРАННЫЙ Виртуальная выставка читального зала гуманитарных наук «Внешнеэкономическая диспозиция России От ВТО до ЕЭП»
«Внешнеэкономическая диспозиция России От ВТО до ЕЭП» Шестое поколение мобильной связи
Шестое поколение мобильной связи Неделя карьеры ПАО КРИОГЕНМАШ
Неделя карьеры ПАО КРИОГЕНМАШ Презентация на тему Принтеры
Презентация на тему Принтеры Анне Андреевне Иващенко по случаю славного юбилея ОДА
Анне Андреевне Иващенко по случаю славного юбилея ОДА Виды общения
Виды общения