Представление чисел в памяти компьютера

Как представляются в компьютере целые числа?
Целые числа могут представляться в компьютере со знаком или без знака.
Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 000000002 до 111111112 , а в двубайтовом формате - от 00000000 000000002 до 11111111111111112.

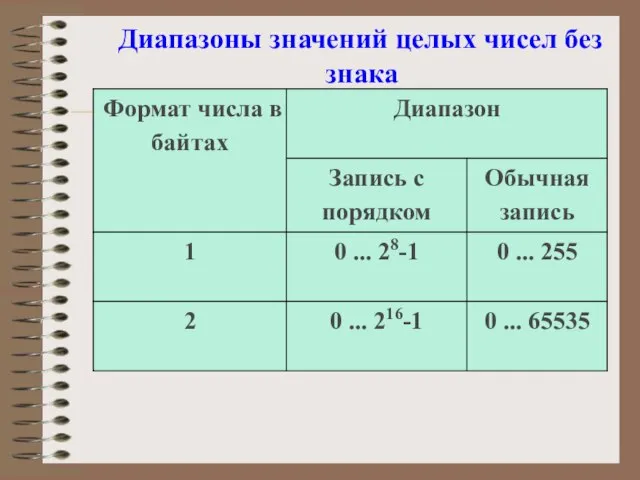
Диапазоны значений целых чисел без знака

Число 3910 = 100111 2 в однобайтовом формате:
Число 3910 = 100111 2 в двубайтовом формате:
Число 65 53510 = 11111111 111111112 в двубайтовом формате:

Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак "плюс" кодируется нулем, а "минус" - единицей.
Диапазоны значений целых чисел со знаком

Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится один разряд, а для цифр абсолютной величины - семь разрядов.
В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код.

Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково - двоичными кодами с цифрой 0 в знаковом разряде.
Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа - двоичный код его абсолютной величины

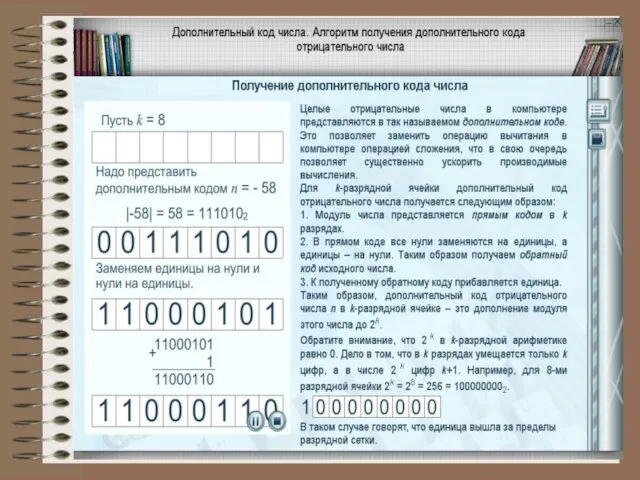
2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы –нулями.
3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.

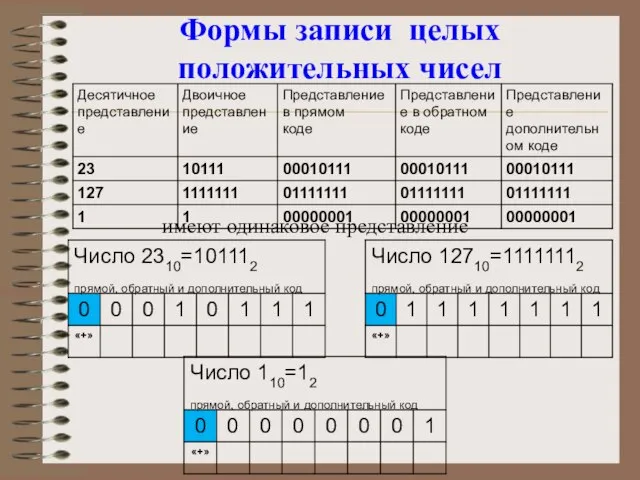
Формы записи целых положительных чисел
имеют одинаковое представление

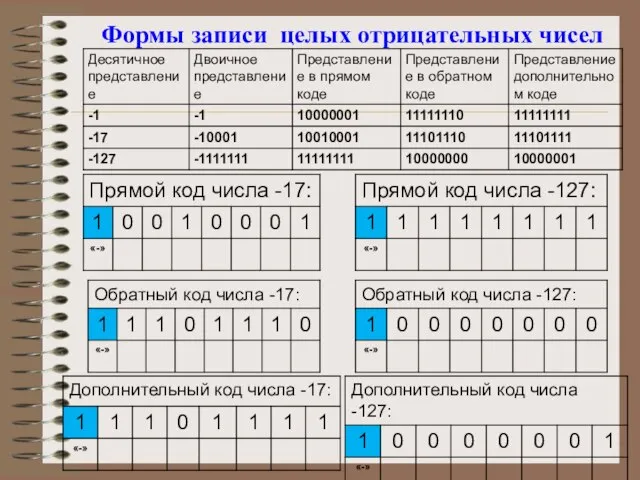
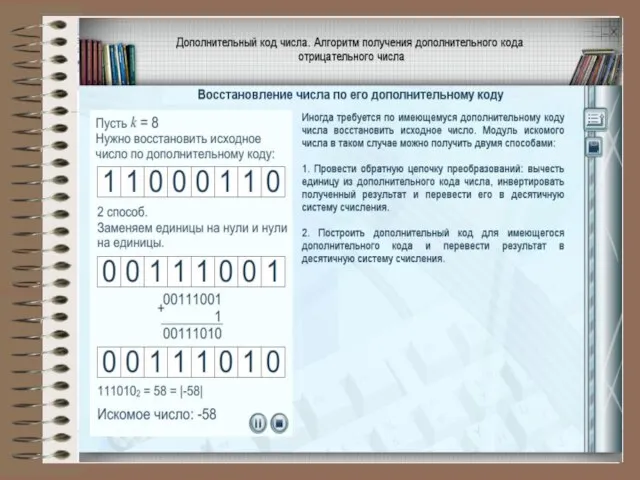
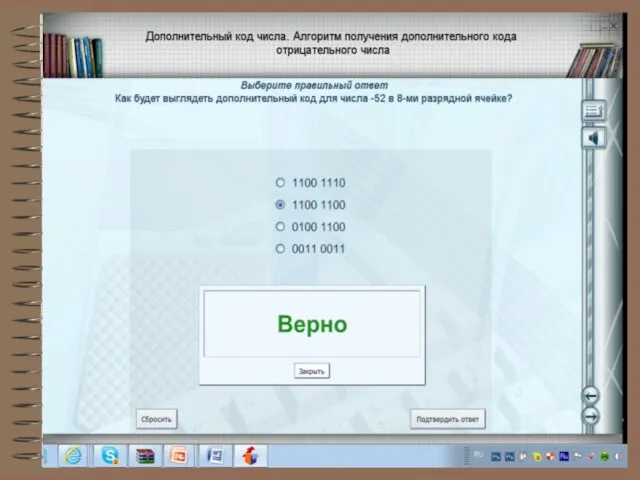
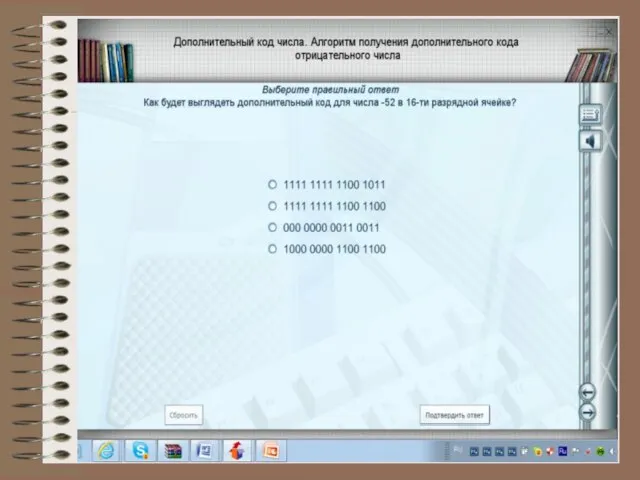
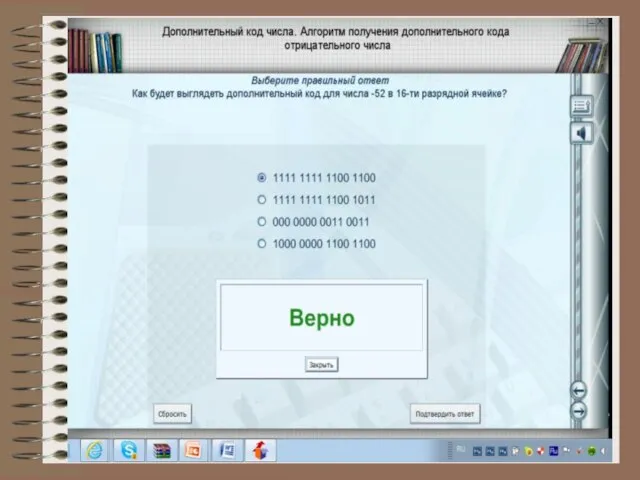
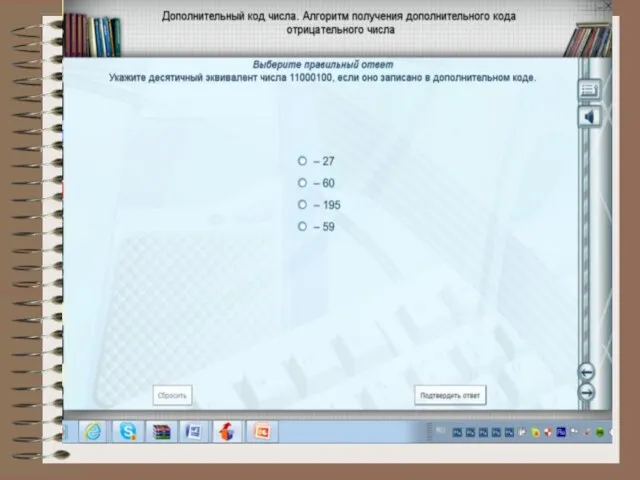
Формы записи целых отрицательных чисел

Операции над числами с фиксированной точкой.

1. А и В положительные. При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например:
Получен правильный результат.

2. А положительное, B отрицательное и по абсолютной величине больше, чем А.
Например:
Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируются: 1 0000111 = –710.

3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:
Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы!!!

4. А и В отрицательные. Например:
Полученный первоначально неправильный результат (обратный код числа –1110 вместо обратного кода числа –1010) компьютер исправляет переносом единицы из знакового разряда в младший разряд суммы.
При переводе результата в прямой код биты цифровой части числа инвертируются: 1 0001010 = –1010.

5. А и В положительные, сумма А+В больше, либо равна 2n–1, где n – количество разрядов формата чисел (для однобайтового формата n=8, 2n–1 = 27 = 128). Например:
Семи разрядов цифровой части числового формата недостаточно для размещения восьмиразрядной суммы (16210 = 101000102), поэтому старший разряд суммы оказывается в знаковом разряде. Это вызывает несовпадение знака суммы и знаков слагаемых (знак суммы – отрицателен, знак слагаемых – положительный), что является свидетельством переполнения разрядной сетки.

6. А и В отрицательные, сумма абсолютных величин А и В больше, либо равна 2n–1.
Например:
632 =01111112
Здесь знак суммы тоже не совпадает со знаками слагаемых, что свидетельствует о переполнении разрядной сетки.

1. А и В положительные. Здесь нет отличий от случая 1, рассмотренного для обратного кода, т.к. дополнительный код используется только для отрицательных чисел.

2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:
Получен правильный результат в дополнительном коде.
При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 1 0000110 + 1 = 1 0000111 = –710.

3. А положительное, B отрицательное и по абсолютной величине меньше, чем А.
Например:
Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.

4. А и В отрицательные.
Например:
Получен правильный результат в дополнительном коде. Единицу переноса из знакового разряда компьютер отбрасывает. Случаи переполнения для дополнительных кодов рассматриваются по аналогии со случаями 5 и 6 для обратных кодов.

Задача.
Выполнить действия над машинными кодами чисел:
с фиксированной точкой. Формат 16 двоичных разрядов.
Дано: А=190; В=250
Найти: С1=А + В; С2=А – В.
Решение:
А(10) = 190; А(16)=BE=10111110(2)
В(10) = 250; В(16)=FA=11111010(2)
С1 = А+В С2 = А – В
А= 0 000000010111110 А = 0 0000000010111110 (прямой код)
+В= 0 000000011111010 - В = 1 111111100000110
(дополнительный код)
С1= 0 000000110111000 С2 = 1 111111111000100
Проверка: Проверка:
С1=110111000(2) С2 = - 111100 = - BC= - 3*16 +12*1 =
= - 60 (10)
С1(16) = 1В8 = 1*16*16+11*16+8*1 = 440(10)
Ответ:
С1 = 0 000000110111000
С2 = 1 000000000111100

Задача.
Выполнить действия над машинными кодами чисел:
с фиксированной точкой.
Формат 16 двоичных разрядов.
Дано: А= - 387; В= - 128
Найти: С1=А + В;
Решение:
X = A+B X = (-A) + ( - B)
А(10) = - 387; А(16)=- 183(16)= - 110000011(2)
В(10) = - 128; В(16)=- 80(16)= - 10000000(2)
A(2) = 1 000000110000011 –прямой код
А(2) = 1 111111001111100 –обратный код
А(2) = 1 111111001111101 – дополн. код

В(2) = 1 000000010000000 – прямой код
В(2) = 1 111111101111111 – обратный код
В(2) = 1 111111110000000 – дополн.код
(-А) = 1 111111001111101
+ (-В) = 1 111111110000000
Х = 1 111110111111101 –доп. код
Х = 1 000001000000010 – обр.код
Х = 1 000001000000011 – пр.код
Х = - 203(16) = - (2*16*16+0*16+3*1) =
= - (256*2+3) = - (512+3)+ - 515

Представление чисел с плавающей точкой.
Этот способ представления опирается на нормализованную (экспоненциальную) запись действительных чисел.
Нормализованная запись отличного от нуля действительного числа A - это запись вида:
А= m* qn,
где m – мантисса числа (правильная дробь, у которой первая цифра после запятой не равна нулю),
q – основание системы,
n – порядок числа.

Примеры:
1. Мантисса числа 64.5 – это число 0.645, а порядок – число 2, так как 64.5 = 0.645*10 степень (2).
2. Мантисса числа 0.0000012 – это число 0.12, а порядок – число -5, потому что 0.0000012= =0.12*10 степень(-5).
При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды - для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы.

Операции над числами с плавающей точкой.

Дано:А = 12,75; В = 250
Найти: С3 = А + В, С4 = А – В
Формат – 32 двоичных разряда со смещенным порядком.
А(10) = 12,75 = А(16) = С.С;
В(10) = 250 = В(16) = FA
Нормализация мантисс
mA = 0.CC; pxA = 40 + 1 = 41
mB = 0.FA; pxB = 40 + 2 = 42
Выравнивание характеристик:
∆p = pxA – pxB = -1
m*A = mA * 16 -1 = 0.0CC;
pxA = 41+ 1 = 42
C3 = A + B;
mA = 00 0CC000 pxA = 42
mB = 00 FA0000 pxB = 42
mC3 = 01 06C000 pxC = 42

Нормализация мантиссы результата
mxC3 = 00 106C00;
pxC3 = 42 + 1 = 43
Проверка
С3(16) = 106,C = (C3) = 262,75
C3 = 0 1000011000100000110110000000000
C4 = A – B
mA = 00 0CC000 pxA = 42
mB = 10 06000 pxB = 42
mC3 = 10 12C000 pxC = 42
Нормализация мантиссы результата:
mС4 = 10 ED4000 pxC4 = 42
Проверка:
С4 = - ED.4 = (C4) = - (14 * 16 + 13 * 1 + 4/16) = - 237, 25
C4=11000010111011010100000000000000

Задания на дом:
1. Угринович Н.Д. п. 2.9., стр.103-105.
2. Заполнить карточки.