Представление знаний – основа интеллектуальных систем

Гаврилов А.В. НГТУ, каф. АППМ
Представление знаний в системах искусственного интеллекта
Основной особенностью интеллектуальных систем является то, что они основаны на знаниях, а вернее, на некотором их представлении.
Знания здесь понимаются как хранимая информация, формализованная в соответствии с некоторыми правилами, которую ЭВМ может использовать при логическом выводе по определенным алгоритмам.
Наиболее фундаментальной и важной проблемой является описание смыслового содержания проблем самого широкого диапазона, т.е. должна использоваться такая форма описания знаний, которая гарантировала бы правильную обработку их содержимого по некоторым формальным правилам. Эта проблема называется проблемой представления знаний.

Гаврилов А.В. НГТУ, каф. АППМ
Отличие знаний от данных
Более структурированы и связны, т.е. самое важное в знаниях не сами данные, а связи между ними
Более самоинтерпретируемы
Отвечают не только на вопросы «что», «кто», «где», «когда», но и на вопросы «как» и «почему»
Субъективны в отличие от объективности данных
Могут быть противоречивы, не полны и не точны

Гаврилов А.В. НГТУ, каф. АППМ
Методы представления знаний
В настоящее время наиболее используемые подходы к представлению знаний в интеллектуальных системах:
Методы инженерии знаний, ориентированные на формализацию знаний:
логические модели, в том числе продукционные;
семантические сети;
фреймы;
Методы, ориентированные на обучение:
нейронные сети;
байесовские сети (условные вероятности)

Гаврилов А.В. НГТУ, каф. АППМ
Другая классификация методов представления знаний
Логические
Эвристические
Нейронные сети
Вероятностные

Гаврилов А.В. НГТУ, каф. АППМ
Логические
Логика предикатов 1-го порядка
Модальные логики
Нечеткие логики
Псевдофизические логики
Дескрипторная логика

Гаврилов А.В. НГТУ, каф. АППМ
Эвристические
Правила-продукции
Семантические сети
Фреймы

Гаврилов А.В. НГТУ, каф. АППМ
Продукционная модель
Продукционные правила - наиболее простой способ, представления знаний. Он основан на представлении знаний в форме правил, структурированных в соответствии с образцом «ЕСЛИ - ТО». Часть правила «ЕСЛИ» называется посылкой, а «ТО» - выводом или действием. Правило в общем виде записывается так:
ЕСЛИ A1, A2, ...,An, ТО В.
Такая запись означает, что «если все условия от A1 до Аn являются истинными, то В также истинно» или «когда все условия от А1 до Аn выполняются, то следует выполнить действие В».
Рассмотрим правило
ЕСЛИ (1) у является отцом х
(2) z является братом у
ТО z является дядей х

Гаврилов А.В. НГТУ, каф. АППМ
Продукционная модель (2)
Знания, представленные в интеллектуальной системе, образуют базу знаний.
В интеллектуальную систему входит также механизм выводов, который позволяет на основе знаний, имеющихся в базе знаний, решать задачи, для которых построена система, и получать новые знания.

Гаврилов А.В. НГТУ, каф. АППМ
Продукционная модель (пример)
Положим, что в базе знаний вместе с описанным выше правилом содержатся и такие знания:
ЕСЛИ (1) z является отцом х
(2) z является отцом у
(3) х и у не являются одним и тем же человеком
ТО х и у являются братьями
Иван является отцом Сергея
Иван является отцом Павла
Сергей является отцом Николая
Следовательно ? Павел является дядей Николая

Гаврилов А.В. НГТУ, каф. АППМ
Интеллектуальная система, основанная на знаниях включает в себя:
Базу знаний:
Формализованные знания, упорядоченные и закреплённые на материальном носителе
Формализованные метазнания, включая знания о достоверности источников знаний
Программное обеспечение, обеспечивающее:
доступ к знаниям
пополнение знаний (обучение)
использование знаний для решения практических задач

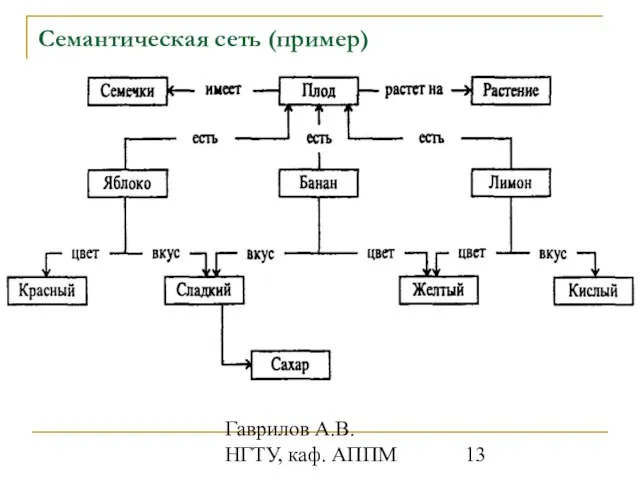
Гаврилов А.В. НГТУ, каф. АППМ
Семантическая сеть
Семантическая сеть - иной подход к представлению знаний, который основан на изображении понятий (сущностей) с помощью точек (узлов) и отношений между ними с помощью дуг на плоскости.
Семантические сети способны отображать структуру знаний во всей сложности их взаимосвязей, увязать в единое целое объекты и их свойства.
В качестве примера может быть приведена часть семантической сети, относящейся к понятию «фрукты».

Гаврилов А.В. НГТУ, каф. АППМ
Семантическая сеть (пример)

Гаврилов А.В. НГТУ, каф. АППМ
Фреймы
Фреймовая система имеет все свойства, присущие языку представления знаний, и одновременно являет собой новый способ обработки информации.
Слово «фрейм» в переводе с английского языка означает «рамка».

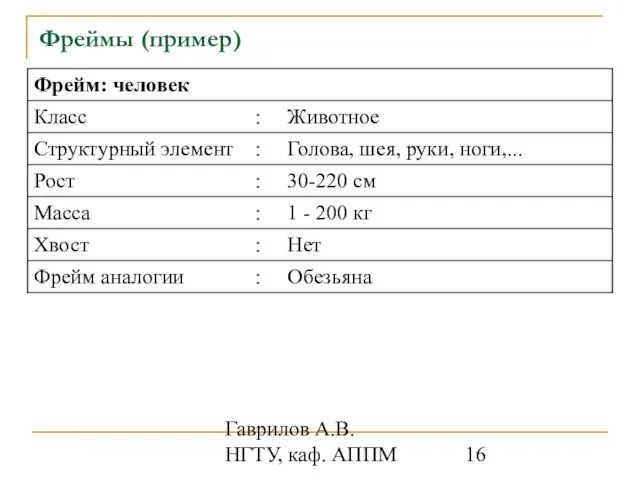
Гаврилов А.В. НГТУ, каф. АППМ
Фреймы (2)
Фрейм является единицей представления знаний об объекте, которую можно описать некоторой совокупностью понятий и сущностей.
Фрейм имеет определенную внутреннюю структуру, состоящую из множества элементов, называемых слотами.
Каждый слот, в свою очередь, представляется определенной структурой данных, процедурой, или может быть связан с другим фреймом.

Гаврилов А.В. НГТУ, каф. АППМ
Фреймы (пример)

Гаврилов А.В. НГТУ, каф. АППМ
Особенности машинного представления знаний
Внутренняя интерпретируемость. Обеспечивается наличием у каждой информационной единицы своего уникального имени, по которому система находит ее для ответа на запросы, в которых это имя упомянуто.
Структурированность. Информационные единицы должны обладать гибкой структурой, для них должен выполняться «принцип матрешки», т.е. вложенности одних информационных единиц в другие, должна существовать возможность установления соотношений типа «часть - целое», «род - вид», «элемент - класс» между отдельными информационными единицами.
Связность. Должна быть предусмотрена возможность установления связей различного типа между информационными единицами, которые бы характеризовали отношения между информационными единицами. Эти отношения могут быть как декларативными (описательными), так и процедурными (функциональными).

Гаврилов А.В. НГТУ, каф. АППМ
Особенности машинного представления знаний (2)
Семантическая метрика. Позволяет устанавливать ситуационную близость информационных единиц, т.е. величину ассоциативной связи между ними. Такая близость позволяет выделять в знаниях некоторые типовые ситуации, строить аналогии.
Активность. Выполнение действий в интеллектуальной системе должно инициироваться не какими-либо внешними причинами, а текущим состоянием представленных в системе знаний. Появление новых фактов или описание событий, установление связей должны стать источником активности системы.

Гаврилов А.В. НГТУ, каф. АППМ
Формализм как средство представления знаний
Формализм – это формальная система, используемая в качестве средства представления знаний
Формализм включает:
языковой (изобразительный) компонент
алфавит и синтаксис
процедурный (алгоритмический, вычислительный) компонент
аксиоматика и продукционные правила, модели рассуждений над знаниями

Гаврилов А.В. НГТУ, каф. АППМ
Моделирование рассуждений
Рассуждение - один из важнейших видов мыслительной деятельности человека, в результате которого он формулирует на основе некоторых предложений, высказываний, суждений новые предложения, высказывания, суждения.
Действительный механизм рассуждений человека остается пока недостаточно исследованным.

Гаврилов А.В. НГТУ, каф. АППМ
Моделирование рассуждений (2)
Человеческим рассуждениям присущи:
неформальность,
нечеткость,
нелогичность,
широкое использование образов, эмоций и чувств, что делает чрезвычайно трудными их исследование и моделирование.
К настоящему времени лучше всего изучены логические рассуждения и разработано много механизмов дедуктивных выводов, реализованных в различных интеллектуальных системах, основанных на представлении знаний с помощью логики предикатов 1-го порядка

Гаврилов А.В. НГТУ, каф. АППМ
Исчисление предикатов первого порядка
применяется
в диагностических и советующих экспертных системах (ЭС)
в системах компьютерного перевода текстов
для реализации символьных преобразований
аналитическое решение уравнений
аналитическое упрощение выражений
аналитическое интегрирование и дифференцирование и т.п.
в качестве метаязыка
в системах, требующих определения специализированных формальных систем для представления специфических знаний
программная реализация
непроцедурный язык программирования Prolog
оболочки ЭС
автоматизация обучения проблематична
как правило, формализация знаний выполняется человеком – инженером по знаниям

Гаврилов А.В. НГТУ, каф. АППМ
Логика предикатов 1-го порядка
Предикат - это конструкция вида P(t1,t2,...,tn), выражающая какую-то связь между некоторыми объектами или свойствами объектов. Обозначение этой связи или свойства, Р, называют «предикатным символом»; t1,t2,...,tn обозначают объекты, связанные свойством (предикатом) Р и называют термами.
Термы могут быть только трех следующих типов:
1) константа (обозначает индивидуальный объект или понятие);
2) переменная (обозначает в разное время различные объекты);
3) составной терм – функция f(t1,t2,...,tn), имеющая в качестве своих аргументов m термов t1,t2,...,tn.

Гаврилов А.В. НГТУ, каф. АППМ
Логика предикатов 1-го порядка (пример)
1. Предложение «Волга впадает в Каспийское море» можно записать в виде предиката
впадает (Волга, Каспийское море).
«Впадает» - предикатный символ; «Волга» и «Каспийское море» - термы-константы. Мы могли обозначить отношение «впадает» и объекты «Волга» и «Каспийское море» символами.
Вместо термов-констант можно рассматривать переменные:
впадает (Х, Каспийское море)
или
впадает (X,Y).
Это тоже предикаты.
2. Отношение х + 1 < у можно записать в виде предиката А(х,у). Предикатный символ А здесь обозначает то, что останется от x + 1 < у, если выбросить из этой записи переменные х и у.

Гаврилов А.В. НГТУ, каф. АППМ
Логика предикатов 1-го порядка.
Формальная (логическая) система

Гаврилов А.В. НГТУ, каф. АППМ
Логика предикатов 1-го порядка
F(x1, x2 … xn) - предикат (логическая функция),
xi - переменная предметной области,
n - арность предиката.
f(x1, x2 … xm) - функция, определенная на области определения xi.

Гаврилов А.В. НГТУ, каф. АППМ
Логика предикатов 1-го порядка
Формула состоит из предикатов, логических связок &, V, ¬, и кванторов всеобщности и существования
Импликация
Из истинности F1(x1) следует истинность F2(x2).

Гаврилов А.В. НГТУ, каф. АППМ
Логика предикатов 1-го порядка
Для всех x предикат F(x) истинен
Существует хотя бы одно такое значение x, при котором предикат F(x) истинен
x - связанная, y - свободная переменные

Гаврилов А.В. НГТУ, каф. АППМ
Логика предикатов 1-го порядка
Для всех x предикат F(x) истинен
Существует хотя бы одно такое значение x, при котором предикат F(x) истинен
x - связанная, y - свободная переменные

Гаврилов А.В. НГТУ, каф. АППМ
Логика предикатов 1-го порядка
Интерпретация
F(x) - свойство объекта x,
зеленый(кузнечик), высокий(столб),
F(x,y) - отношение между объектами x и y,
отец(Иван, Петр), учится(Иванов, НГТУ),
над(облако, земля), выше(башня, дерево),
на_территории(Россия, Байкал).
Решение задачи – логический вывод (доказательство целевого предиката) методом резолюции (доказательство от противного)

Гаврилов А.В. НГТУ, каф. АППМ
Пример 1 программы на Прологе – языке логического программировния
PREDICATES
bird(symbol)
parent(symbol,symbol)
CLAUSES
bird(sparrow). // Воробей – это птица.
bird(X):–parent(Y,X), bird(Y). // X – это птица,
//если у него есть родитель,
//который является птицей.
parent(sparrow,nestling). // Воробей – родитель
// птенца.

Гаврилов А.В. НГТУ, каф. АППМ
Пример 2 программы на Прологе
DOMAINS
name=symbol
PREDICATES
father (name, name)
everybody
CLAUSES
father (“Павел”, “Петр”).
father (“Петр”, “Михаил”).
father (“Петр”, “Иван”).
everybody:- father (X, Y), write (X, “это отец ”, Y, “а”), nl, fail.
GOAL
everybody.

Гаврилов А.В. НГТУ, каф. АППМ
Недостатки логики предикатов
1-го порядка
- монотонность логического вывода, т.е. невозможность пересмотра полученных промежуточных результатов (они считаются фактами, а не гипотезами);
- невозможность применения в качестве параметров предикатов других предикатов, т.е. невозможность формулирования знаний о знаниях;
- детерминированность логического вывода, т.е. отсутствие возможности оперирования с нечеткими знаниями.

Гаврилов А.В. НГТУ, каф. АППМ
Традиционное решение задачи принадлежности множеству
Основано на законах логики, которые, в свою очередь, опираются на два предположения:
для любого элемента и множества элемент либо является членом множества, либо принадлежит дополнению этого множества;
закон исключения третьего — элемент не может одновременно принадлежать множеству и его дополнению.
Классическая теория множеств базируется на булевой, двухзначной логике. Принадлежность объекта к классу а ∈ А может принимать значения ИСТИНА, если объект а входит в множество А, или ЛОЖЬ — в противоположном случае. После появления понятия «нечеткие множества», обычные множества стали также называть «жесткими».

Гаврилов А.В. НГТУ, каф. АППМ
Проблема нечеткой принадлежности
В реальных ситуациях редко встречаются объекты, которые точно соответствуют той или иной категории или классу. У конкретного экземпляра часть признаков может присутствовать, а другая часть отсутствовать. Таким образом, принадлежность этого объекта к какому-либо классу является размытой.
Для формирования суждений о подобных категориях и принадлежащих к ним объектов Лофти Заде (Zadeh) предложил теорию нечетких множеств. Этот формализм нарушает оба предположения классической теории «четких» множеств. Для вычислений на нечетких множествах используется аппарат нечеткой логики, позволяющей использовать понятие неопределенности в логических вычислениях.

Гаврилов А.В. НГТУ, каф. АППМ
Формальное определение нечеткого множества
Нечеткое множество определяется через некоторую базовую шкалу B и функцию принадлежности НМ — μ(x), x∈B, принимающую значения на интервале [0..1]. Таким образом, нечеткое множество B — это совокупность пар вида (x, μ(x)), где x∈B.
Функция принадлежности определяет субъективную степень уверенности эксперта в том, что данное конкретное значение базовой шкалы соответствует определяемому НМ. Эту функцию не стоит путать с вероятностью, носящей объективный характер и подчиняющейся другим математическим зависимостям.

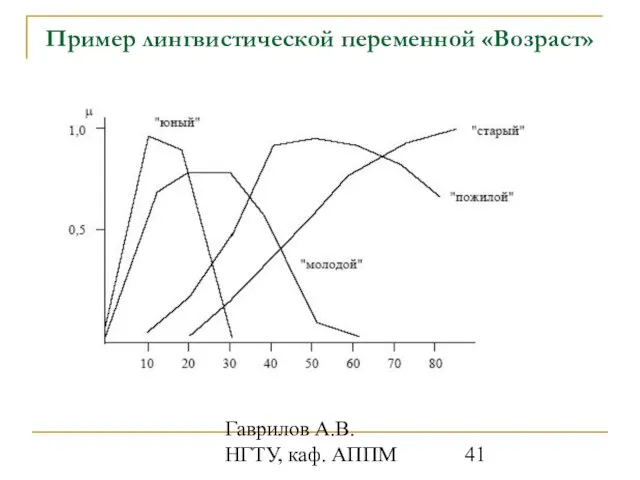
Гаврилов А.В. НГТУ, каф. АППМ
Понятие «лингвистической переменной»
В нечеткой логике вводится понятие лингвистической переменной, значениями которой являются не числа, а слова естественного языка, называемые термами. Например, лингвистическая переменная «скорость» может иметь значения «высокая», «средняя», «очень низкая» и т. д. Фразы, значение которых принимает переменная, в свою очередь, являются именами нечетких переменных. Значения лингвистической переменной (ЛП) определяются через нечеткие множества (НМ), которые, в свою очередь, определены на некотором базовом наборе значений или базовой числовой шкале, имеющей размерность. Каждое значение ЛП определяется как нечеткое множество (например, НМ «низкий рост»).

Гаврилов А.В. НГТУ, каф. АППМ
Формирование НМ «Дорогой автомобиль»
Рассмотрим нечеткую категорию «дорогой автомобиль». В классической теории множество А «дорогих автомобилей» можно сформировать либо перечислением конкретных представителей данного класса, либо введя в рассмотрение характеристическую функцию f, такую, что для любого объекта X:
f(X) = ИСТИНА тогда и только тогда, когда X ∈ A.
Например, эта функция может отбирать только те автомобили, цена которых более 50 000 евро:

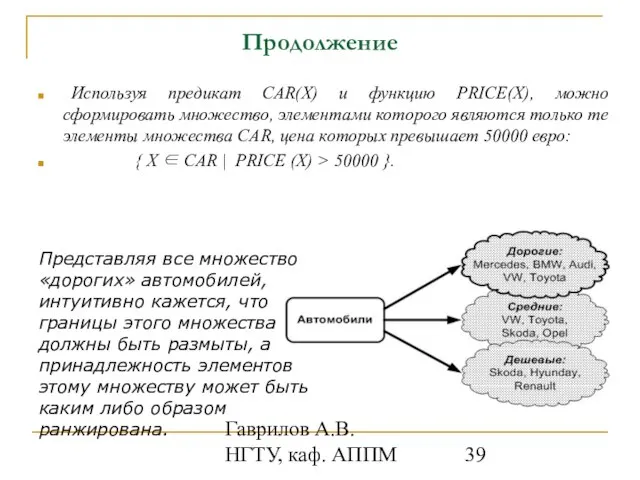
Гаврилов А.В. НГТУ, каф. АППМ
Продолжение
Используя предикат CAR(X) и функцию PRICE(X), можно сформировать множество, элементами которого являются только те элементы множества CAR, цена которых превышает 50000 евро:
{ X ∈ CAR | PRICE (X) > 50000 }.
Представляя все множество «дорогих» автомобилей, интуитивно кажется, что границы этого множества должны быть размыты, а принадлежность элементов этому множеству может быть каким либо образом ранжирована.

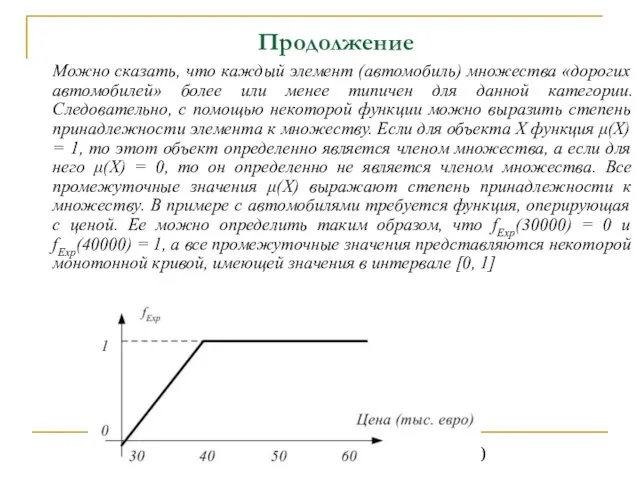
Гаврилов А.В. НГТУ, каф. АППМ
Продолжение
Можно сказать, что каждый элемент (автомобиль) множества «дорогих автомобилей» более или менее типичен для данной категории. Следовательно, с помощью некоторой функции можно выразить степень принадлежности элемента к множеству. Если для объекта X функция μ(X) = 1, то этот объект определенно является членом множества, а если для него μ(X) = 0, то он определенно не является членом множества. Все промежуточные значения μ(X) выражают степень принадлежности к множеству. В примере с автомобилями требуется функция, оперирующая с ценой. Ее можно определить таким образом, что fExp(30000) = 0 и fExp(40000) = 1, а все промежуточные значения представляются некоторой монотонной кривой, имеющей значения в интервале [0, 1]

Гаврилов А.В. НГТУ, каф. АППМ
Пример лингвистической переменной «Возраст»

Гаврилов А.В. НГТУ, каф. АППМ
Логический вывод в нечеткой логике
При решении задач используя нечеткую логику надо в процессе логического вывода продвигать оценку нечеткости к полученному решению.
При этом для каждого промежуточного решения (доказанного предиката) вычисляется значение достоверности (функции принадлежности), используя аналоги операций дизъюнкции и конъюнкции

Гаврилов А.В. НГТУ, каф. АППМ
Нечеткие логические операции в нечеткой логике
Аналоги операций конъюнкции и дизъюнкции в нечеткой логике имеют следующие определения:
fF ∧ G(X) = min(fF(X), fG(X)),
fF ∨ G(X) = max(fF(X), fG(X)).
¬F(X) = 1 – F(X),

Гаврилов А.В. НГТУ, каф. АППМ
Формализм условных вероятностей
применяется
в спам-фильтрах
в диагностических ЭС
если для объекта характерна неполнота или недостаточная достоверность данных
программная реализация
Bayes Net Learner
обучение легко поддаётся автоматизации
Условные вероятности

Гаврилов А.В. НГТУ, каф. АППМ
Нейронные сети
применяются для решения задач:
краткосрочного экономического прогнозирования
в т.ч. для прогнозирования курсов ценных бумаг, валют, оценки рисков кризисов
распознавания образов
освобождения информационного сигнала от помех
программная реализация
OWL
VieNet
NeuroPro
обучение поддаётся автоматизации
но требует больших вычислительных ресурсов
Нейронные сети

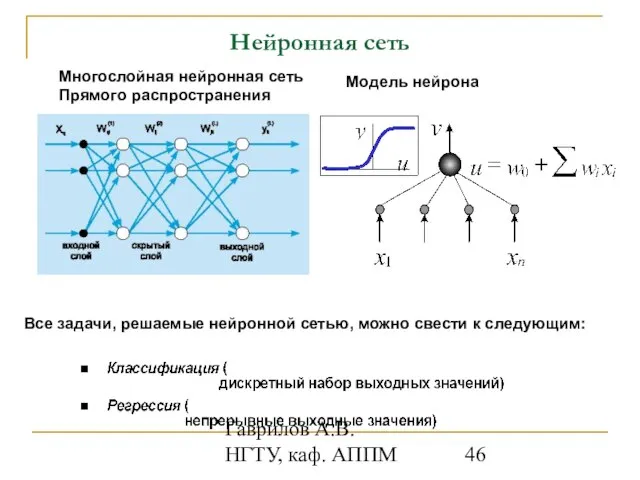
Гаврилов А.В. НГТУ, каф. АППМ
Нейронная сеть
Многослойная нейронная сеть
Прямого распространения
Модель нейрона
Все задачи, решаемые нейронной сетью, можно свести к следующим:

Гаврилов А.В. НГТУ, каф. АППМ
Методы решения задач
Поиск в пространстве состояний
Поиск в глубину
Поиск в ширину ,
Различные эвристики
Логический вывод
Метод резолюции,
Унификация,
Прямой вывод,
Обратный вывод
Ассоциативный поиск
В нейронных сетях

Гаврилов А.В. НГТУ, каф. АППМ
Методы решения задач (2)
Вероятностный вывод
Байесовкие сети
Цепи Маркова
Сопоставление (Matching) описания или образа (pattern) с хранимыми в базе знаний
Структурное (syntactic)
Параметрическое
Семантическое
Детерминированное
Нечеткое
С использованием контекста

Гаврилов А.В. НГТУ, каф. АППМ
Методы решения задач (3)
Все методы решения задач могут рассматриваться как поиск знания, релевантного некоторому паттерну (цели, запросу, входному образу, полученному от сенсоров и т.п.)
Это объясняется происхождением всех методов решения задач от обработки входной сенсорной информации нашим мозгом
Формальные знания и логическая обработка информации основаны на абстрагировании (классификации, кластеризации), т.е. сжатии информации, содержащейся в конкретных образах (сенсорных)