Содержание
- 2. Преобразования фигур Движение Уроки геометрии в 8 классе
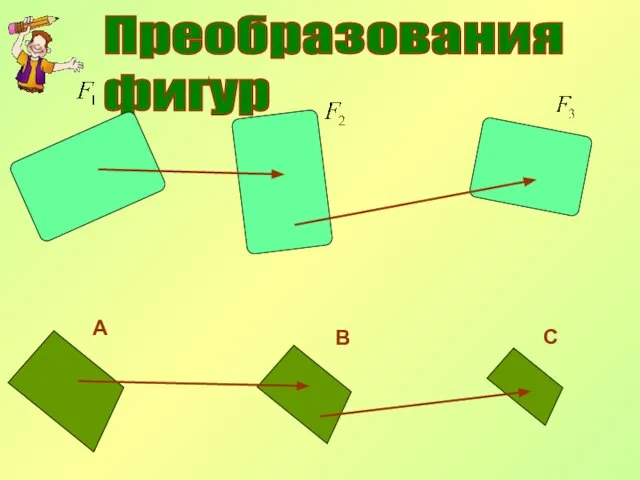
- 3. Преобразования фигур А В С
- 4. Движение Преобразование одной фигуры в другую, при котором сохраняется расстояние между точками называется движением.
- 5. .А .А
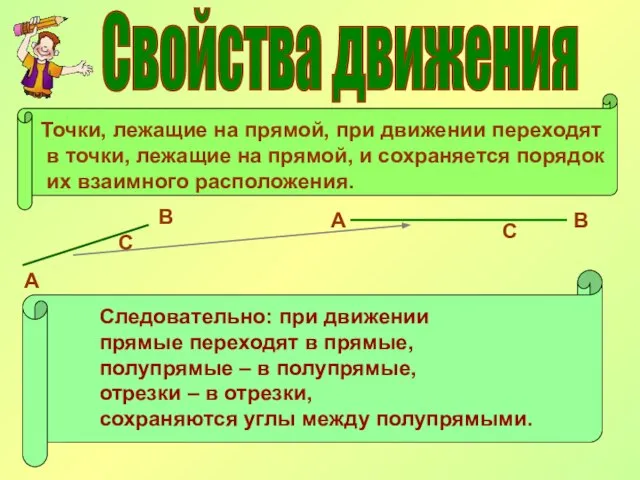
- 6. Свойства движения Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется
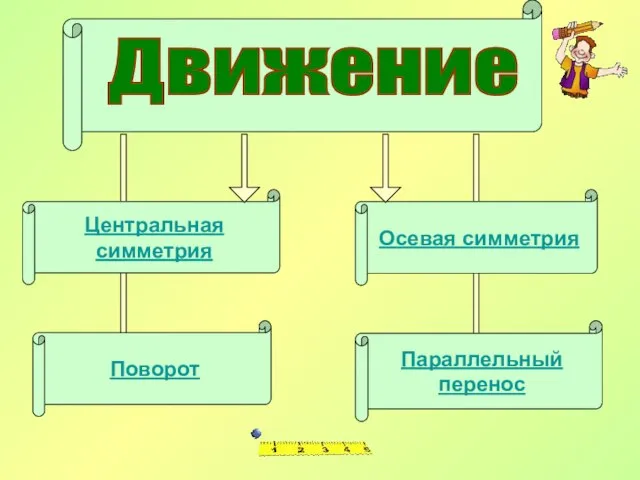
- 7. Движение Центральная симметрия Поворот Осевая симметрия Параллельный перенос
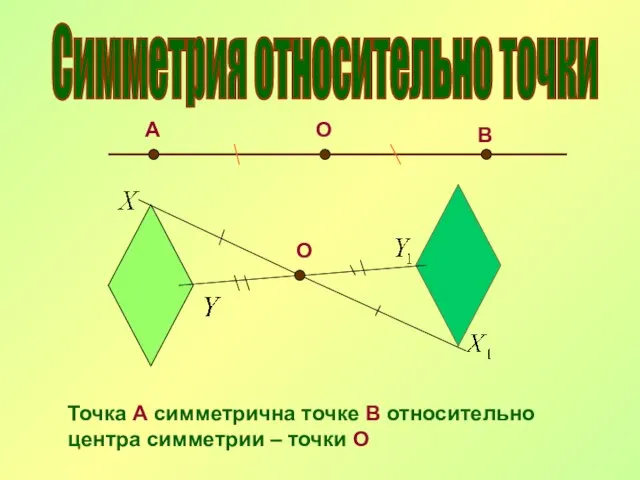
- 8. Симметрия относительно точки О А В О Точка А симметрична точке В относительно центра симметрии –
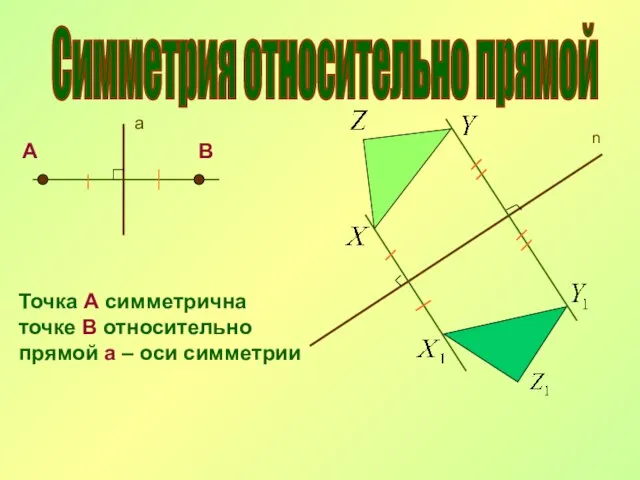
- 10. Симметрия относительно прямой а А В Точка А симметрична точке В относительно прямой а – оси
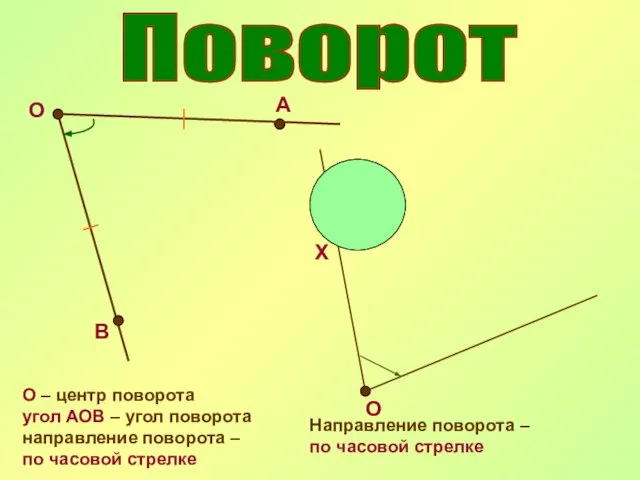
- 12. Поворот О А В О – центр поворота угол АОВ – угол поворота направление поворота –
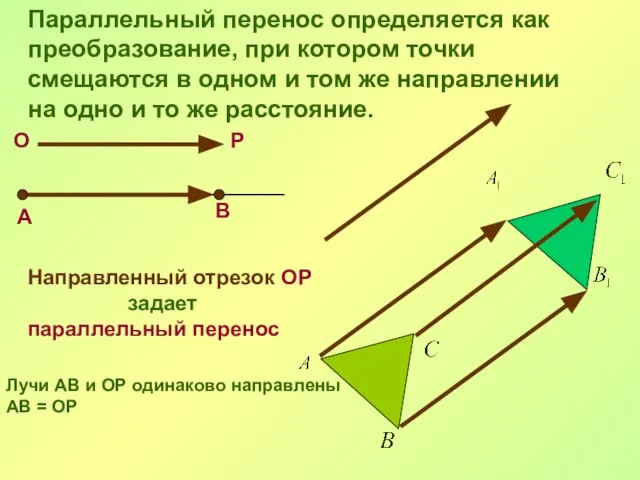
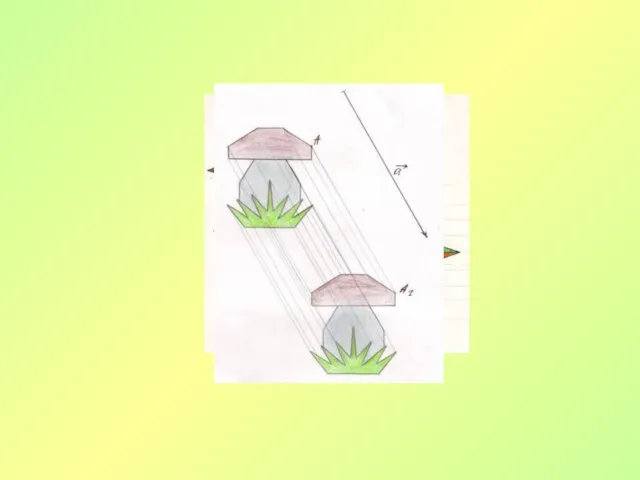
- 14. Параллельный перенос Преобразование фигуры F, при котором ее произвольная точка (х; у) переходит в точку (х+а;
- 15. В О Р А Направленный отрезок ОР задает параллельный перенос Лучи АВ и ОР одинаково направлены
- 17. Композиция движений
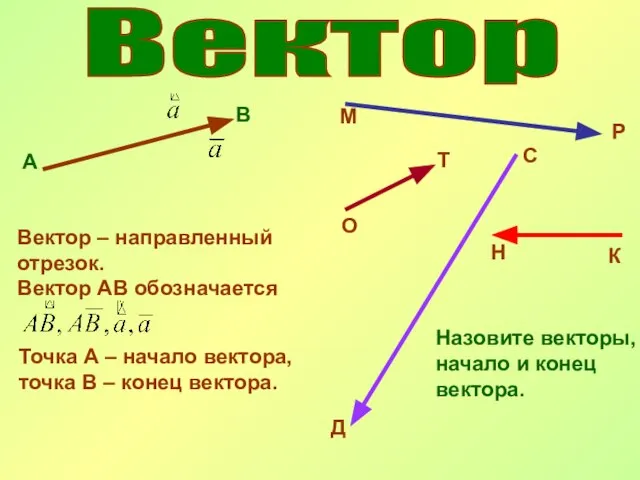
- 18. Вектор А В Вектор – направленный отрезок. Вектор АВ обозначается Точка А – начало вектора, точка
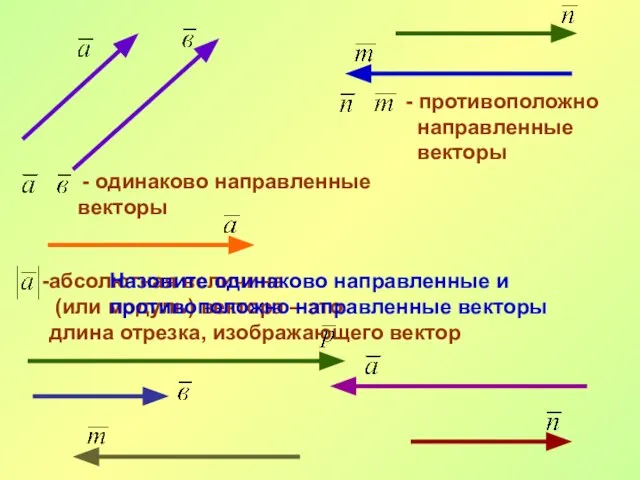
- 19. - одинаково направленные векторы - противоположно направленные векторы абсолютная величина (или модуль) вектора – это длина
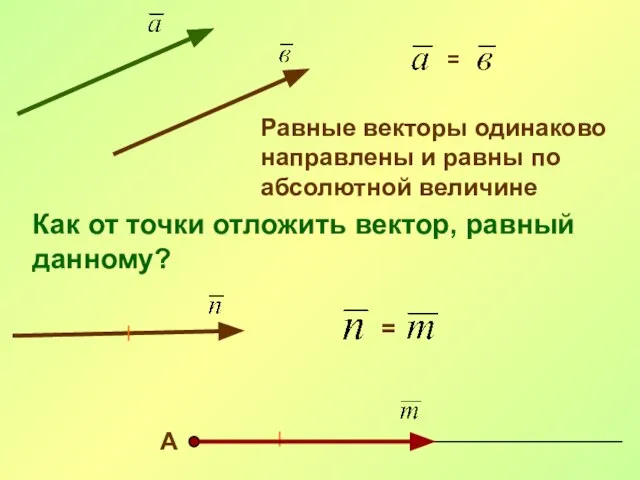
- 20. = Равные векторы одинаково направлены и равны по абсолютной величине Как от точки отложить вектор, равный
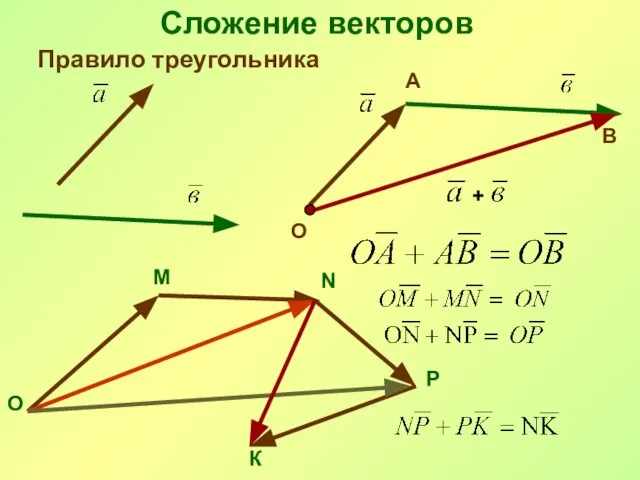
- 21. Сложение векторов Правило треугольника + О А В О М N Р К
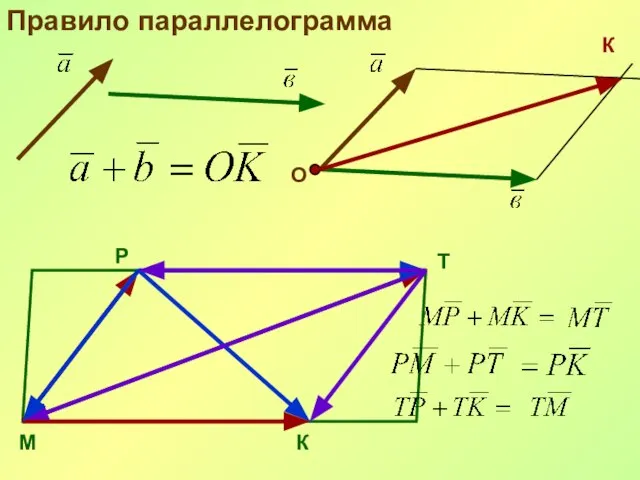
- 22. Правило параллелограмма О К М Р Т К
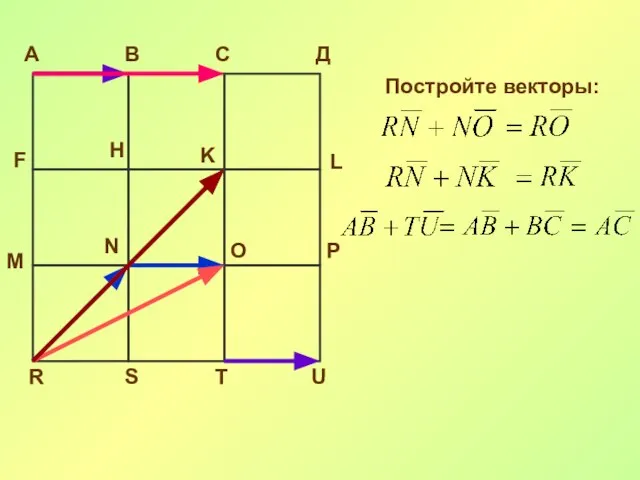
- 23. А В С Д F H K L M N O P R S T U
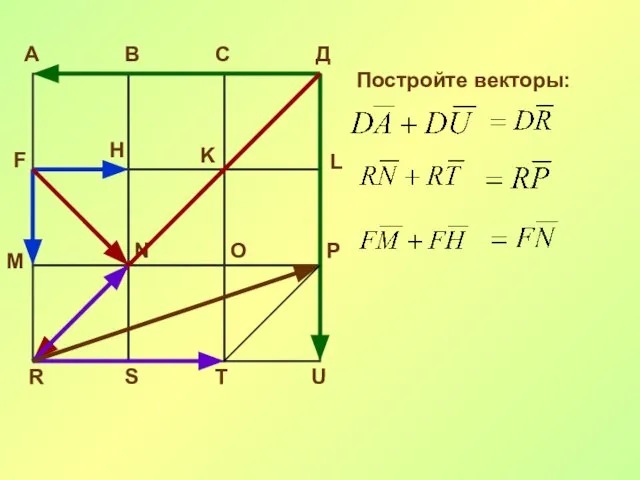
- 24. А В С Д F H K L M N O P R S T U
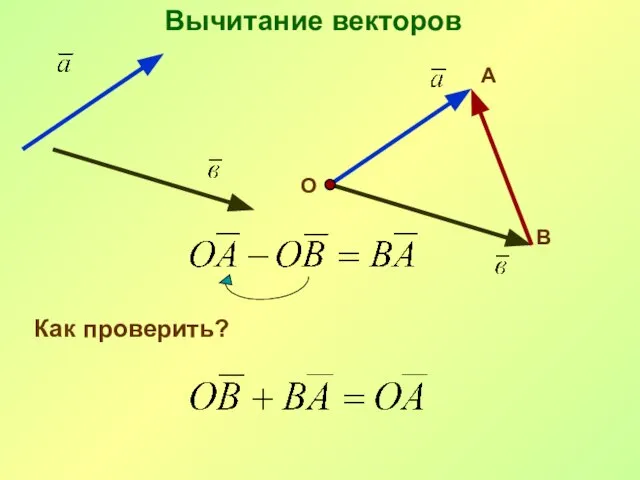
- 25. Вычитание векторов О А В Как проверить?
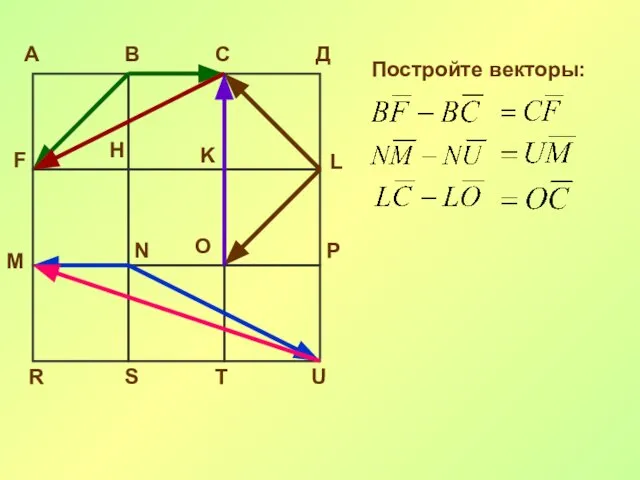
- 26. А В С Д F H K L M N O P R S T U
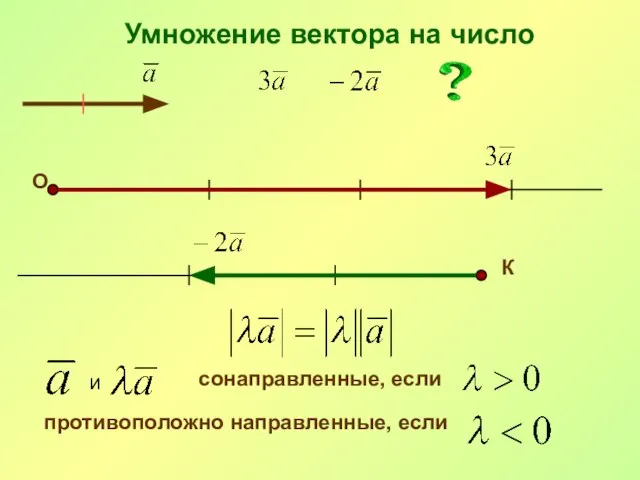
- 27. Умножение вектора на число О К и сонаправленные, если противоположно направленные, если
- 29. Скачать презентацию







 Заболел и в январе 1878 года умер отец. Дмитрий остался единственным кормильцем большой семьи. В поисках работы, а также чтобы дать об
Заболел и в январе 1878 года умер отец. Дмитрий остался единственным кормильцем большой семьи. В поисках работы, а также чтобы дать об Очі епохЧастина ІУкраїна
Очі епохЧастина ІУкраїна Особенности базового курса органической химии издательства «ОЛМА»
Особенности базового курса органической химии издательства «ОЛМА» Тема: «Самородок янтарного края» . Авторы работы: Бакеева Екатерина Рафаиловна, 9 «А» класс, МБОУ Побединской СОШ, п. Чернышевское.
Тема: «Самородок янтарного края» . Авторы работы: Бакеева Екатерина Рафаиловна, 9 «А» класс, МБОУ Побединской СОШ, п. Чернышевское. TERRITORIAL VARIETIES OF ENGLISH PRONUNCIATION
TERRITORIAL VARIETIES OF ENGLISH PRONUNCIATION БЕЗУДАРНЫЕ ГЛАСНЫЕ В КОРНЕ СЛОВА
БЕЗУДАРНЫЕ ГЛАСНЫЕ В КОРНЕ СЛОВА Муниципальное дошкольное образовательное учреждение детский сад комбинированного вида №!2 г. Сердобска
Муниципальное дошкольное образовательное учреждение детский сад комбинированного вида №!2 г. Сердобска Windows Server 2003 R2
Windows Server 2003 R2 Матрешка. Происхождение матрешки
Матрешка. Происхождение матрешки Управление доставкой товараред.2.0
Управление доставкой товараред.2.0 Государственная программа субсидирования ставок на покупку автомобилей отечественного производства
Государственная программа субсидирования ставок на покупку автомобилей отечественного производства Testing times
Testing times PTE –Pearson Test of English
PTE –Pearson Test of English Великий, могучий русский язык. Агитационная акция С книгой в 21 век
Великий, могучий русский язык. Агитационная акция С книгой в 21 век Происхождение государства и права
Происхождение государства и права История первой газеты и журнала
История первой газеты и журнала Порядок. Прогресс. Успех
Порядок. Прогресс. Успех Теорема Виета
Теорема Виета Верные и преданные друзья
Верные и преданные друзья Проектирование организаций
Проектирование организаций Презентация Microsoft PowerPoint (2)
Презентация Microsoft PowerPoint (2) Зависимость стиля общения от свойств темперамента
Зависимость стиля общения от свойств темперамента Моя Родина — Россия
Моя Родина — Россия Жиры.Сложные эфиры глицерина и высших карбоновых кислот
Жиры.Сложные эфиры глицерина и высших карбоновых кислот Блюда из яиц
Блюда из яиц Жилой комплекс Позитив
Жилой комплекс Позитив Портфолио воспитателя
Портфолио воспитателя История становления и развития народного театра в Верховажье в советские годы
История становления и развития народного театра в Верховажье в советские годы