ТЕОРИЯ РИСКА

Литература
Королев В.Ю., Бенинг В.Е., Шоргин С.Я. Математические основы теории риска. М. Физматлит, 2007.
Булинская Е.В. Теория риска и перестрахование. Учебное пособие. В 2 ч. - М.: Изд-во ММФ МГУ, 2001.
Мак Т. Математика рискового страхования. М.: Олимп-Бизнес, 2005.
Фалин Г.И. Математический анализ рисков в страховании. М.: Российский юридический издательский дом, 1994.
Фалин Г.И. Математические основы теории страховании жизни и пенсионных схем. М.: Изд-во Моск. ун-та, 1996.
Гербер Х. Математика страхования жизни. Пер. с англ./ под ред. Бирюкова П.А. – М.: Мир, 1995 г. 154 с.
Bowers, N.L., Gerber, H.U., Hickman, J.C., Jones, D.A., and Nesbitt, C.J.: Actuarial Mathematics. 2nd ed., Society of Actuaries. Schaumburg, Illinois, 1997.
C. D. Daykin, T.Pentikainen, M.Pesonen Practical Risk Theory for Actuaries. - Chapman and Hall, 1994.
Kaas R., Goovaerts M., Dhaene J., Denuit M. Modern Actuarial Risk Theory. Springer. 2008. 381 p.

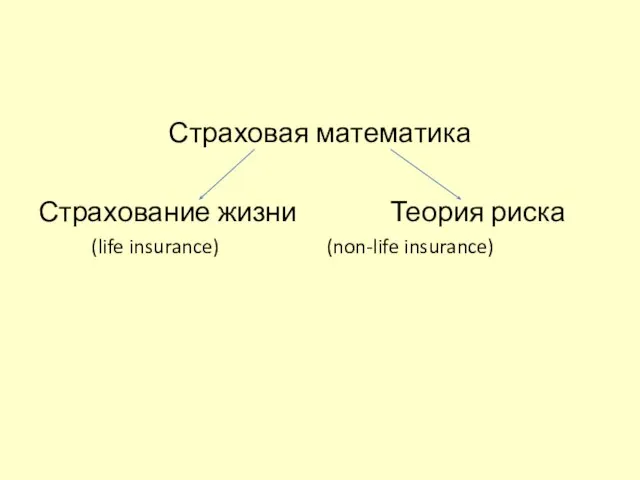
Страховая математика
Страхование жизни Теория риска
(life insurance) (non-life insurance)

Страхователь:
До заключения договора – риск, приводящий к потерям X
После заключения – избавил себя от риска
p – сумма, которую заплатил с.к.
Риск страховой компании Оценка риска

Проблема обеспечения финансовой устойчивости с.к. – комплексная.
В рамках ТР разработана система понятий, моделей и методов, которые позволяют количественно оценивать фин. риски.
ТР входит в квал. экзамен актуариев:
экз.1 «Математические основы актуарной науки»;
экз.3 «Актуарные модели»;
экз.4 «Построение актуарных моделей».

Основные характерные черты ситуаций, связанных с риском
случайный характер события, при котором возможны несколько исходов;
наличие альтернативных решений;
вероятность получения прибыли или возникновения убытков

Употребление слова «риск»
вероятность получения прибыли или возникновения убытков
вероятность возможных потерь, их размер, локализация и т.п. — характеристики рискованной ситуации.

Определение
РИСК (франц.),
в страховом деле: опасность, от которой производится страхование; иногда размер ответственности страховщика. Страхование м. б. произведено против Р. наступления смерти, пожара, градобития и т. п. За Р., который несет страховое учреждение (об-во), страхователь уплачивает страховую премию.
Различного рода случайности, сопряженные с деятельностью предпринимателя и обусловленные изменчивостью рыночной конъюнктуры.
В переносном смысле: действие наудачу; дело, пред- принятое на счастливую случайность. Рисковать – подвергать себя случайности, опасности.
Малая советская энциклопедия, ОГИЗ РСФСР, Москва, 1932.

Страховые риски
риски, поступающие от страхователей
- собственные риски
технические
инвестиционные
нетехнические

Традиционные модели и задачи ТР
Элементарная составляющая страховщика - индивидуальный риск (страховое требование claim) равный итоговой сумме средств, выплаченных по некоторому договору страхования.
Убыток- условное значение величины иска при условии, что иск отличен от 0.

Классификация моделей риска
Модель индивидуальных потерь (статическая модель страхования)
совокупность объектов сформирована единовременно,
страховые премии собраны в момент формирования портфеля,
срок действия всех договоров одинаковый
в течении срока м. происходить стр. события, приводящие к убыткам с.к.

Классификация моделей риска
Модель коллективного риска (динамическая модель страхования)
договоры заключаются в моменты времени, образующие некоторый случайный процесс,
каждый договор имеет свою длительность,
в течении действия договора м. происходить стр. события, приводящие к убыткам с.к.

Задачи ТР
Вычисление распределения суммарного иска
по итогам страх. деятельности по всему портфелю (инд. модель)
по итогам страх. деятельности в течении некоторого интервала времени (колл. модель)

Задачи ТР

Страховая премия – часть полного взноса страхователя (брутто-премии), которая зачисляется в страховой фонд, т.е. в фонд, предназначенный для покрытия будущих страховых выплат

Для модели ИР
Достаточно рассмотреть итоговые суммы убытков и страховых премий по всему портфелю

При вычислении ?(?>?)

Основные задачи теории ИР

В литературе внимание обращается на
явное вычисление распределения суммарного иска при заданных распределениях индивидуальных исков,
простейшие асимптотические формулы,
сравнение рисковых ситуаций,
оценивание риска, функций полезности, эмпирических принципов выбора страховых взносов.

Критика подхода, связанного с применением аппроксимаций для распределения суммарного иска.
Главный недостаток - недостаточная точность соответствующих приближенных формул и отсутствие приемлемых оценок точности аппроксимации (Bowers).

Асимптотика распределения случайной величины R
Использование нормальной аппроксимации для распределения суммарного иска не является идеальным подходом, поскольку реальное распределение обладает положительной асимметрией, которой нет у нормального распределения (Bowers).
Выход –использование, например, «сдвинутого» гамма-распределения

Основные задачи теории КР
Под процессом риска мы будем понимать процесс изменения капитала, принадлежащего страховой компании.
Причины изменения капитала:
он увеличивается благодаря поступлению взносов от клиентов (страховых премий)
уменьшается из-за страховых выплат.

Страховые премии описываются детерминированной (неслучайной) функцией времени.
Процесс страховых выплат случайный.
Т.о., процесс риска является стохастическим процессом.

Основная цель изучения процессов риска – оптимизация параметров деятельности страховых компаний, например, страховых тарифов и/или страховые выплат.

Критерии оптимальности
Например,
- определить вероятностное распределение суммарных страховых выплат за рассматриваемый промежуток времени
- вычислить размер страховых премий, гарантирующий желаемый объем резерва с требуемым уровнем достоверности.
методы предельных теорем теории вероятностей
- вероятность разорения (вероятность того, что процесс риска опустится ниже некоторого уровня в течение определенного промежутка времени (конечного иди бесконечного).)
- задачи, связанные с изучением вероятности разорения.

Вероятность разорения рассматривается как функция основных параметров процесса риска.
Э. Ф. Лундберг - первые оценки этой вероятности
Г. Крамер - систематическое изучение вероятности разорения, поведение вероятности разорения в зависимости от величины начального капитала