Содержание
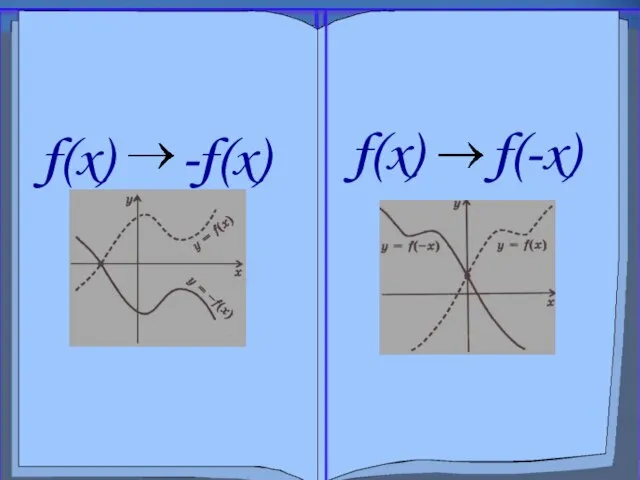
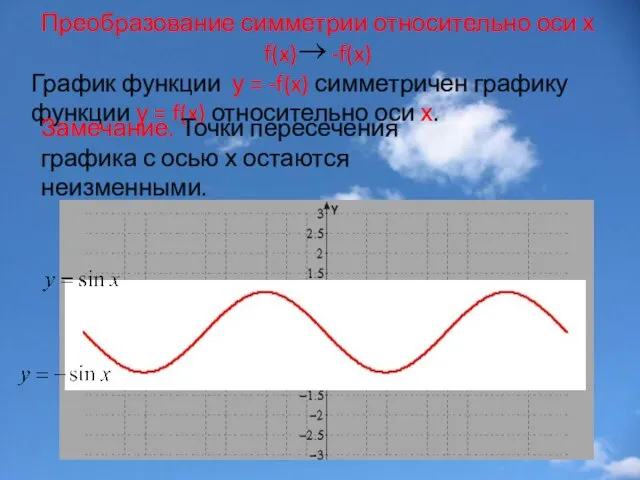
- 3. Преобразование симметрии относительно оси х f(x) -f(x) График функции у = -f(x) симметричен графику функции у
- 5. Преобразование симметрии относительно оси y f(x) f(-x) График функции у = f(-x) симметричен графику функции у
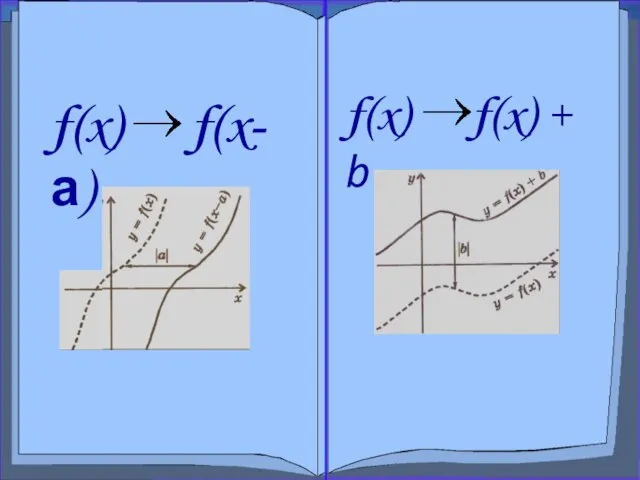
- 7. f(x) f(x) + b
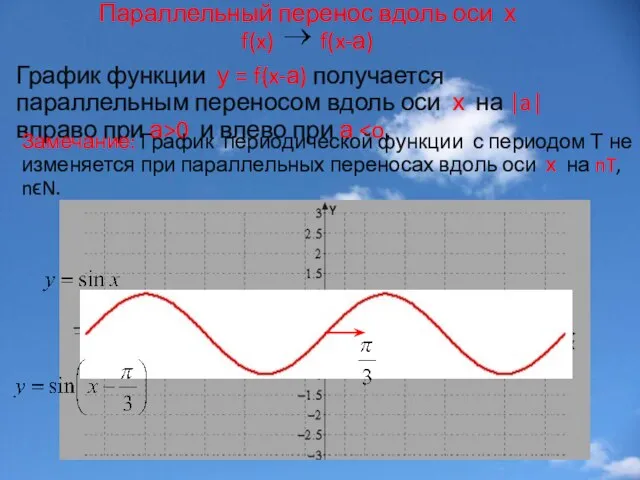
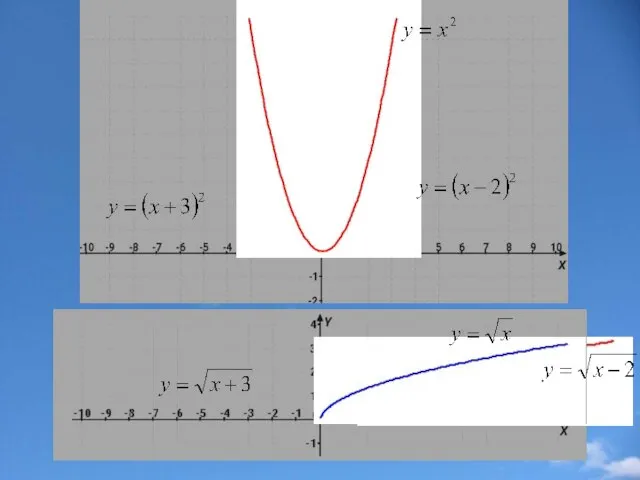
- 8. Параллельный перенос вдоль оси х f(x) f(x-а) График функции у = f(x-а) получается параллельным переносом вдоль
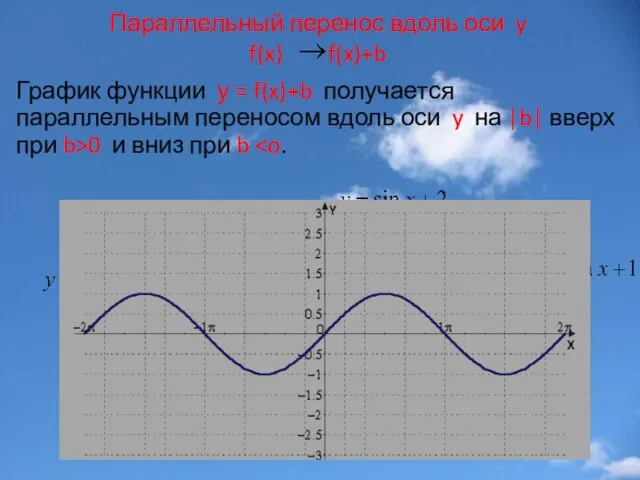
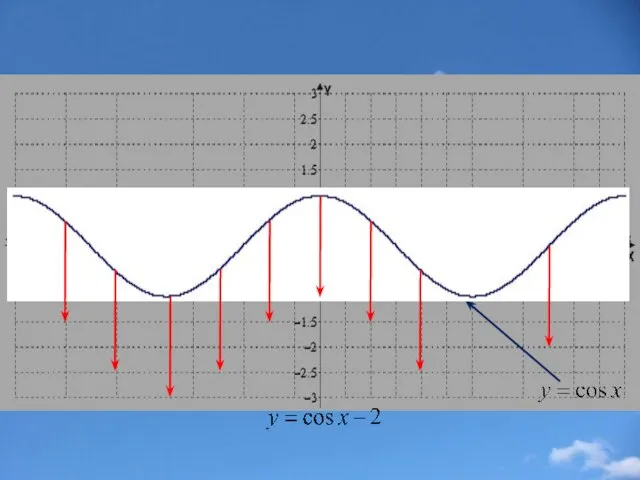
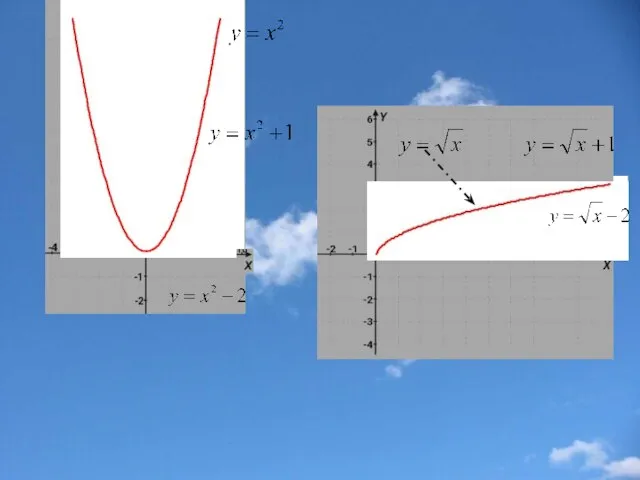
- 10. Параллельный перенос вдоль оси y f(x) f(x)+b График функции у = f(x)+b получается параллельным переносом вдоль
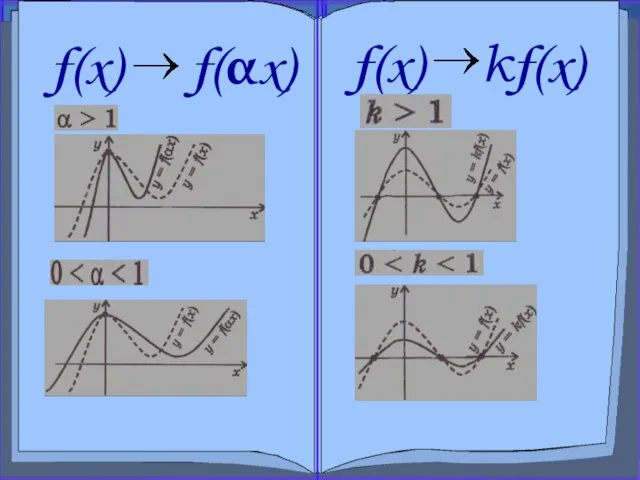
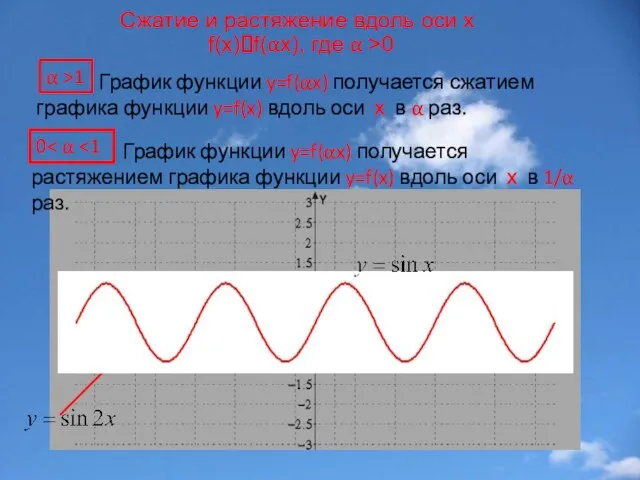
- 14. Сжатие и растяжение вдоль оси x f(x)?f(αx), где α >0 График функции y=f(αx) получается сжатием графика
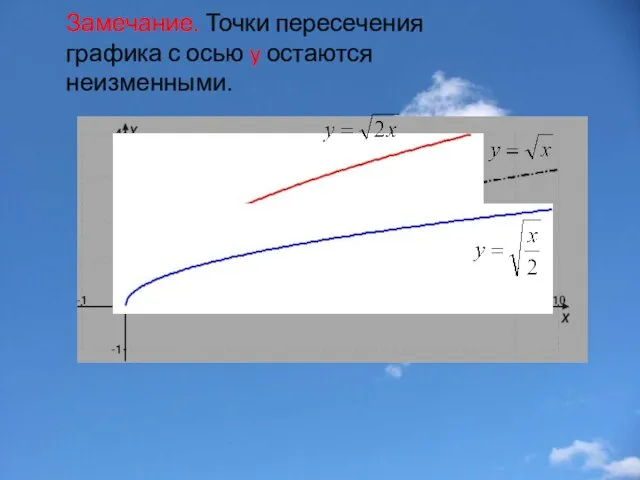
- 15. Замечание. Точки пересечения графика с осью y остаются неизменными.
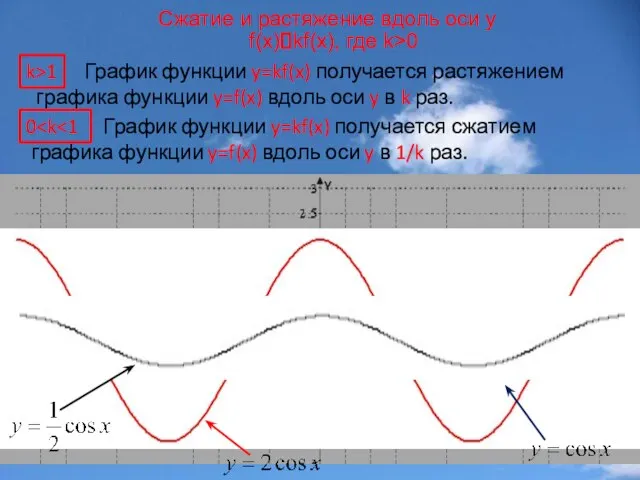
- 16. Сжатие и растяжение вдоль оси y f(x)?kf(x), где k>0 График функции y=kf(x) получается растяжением графика функции
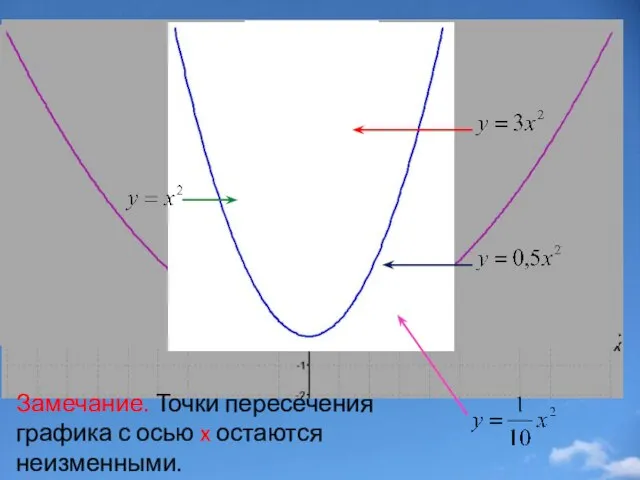
- 18. Замечание. Точки пересечения графика с осью x остаются неизменными.
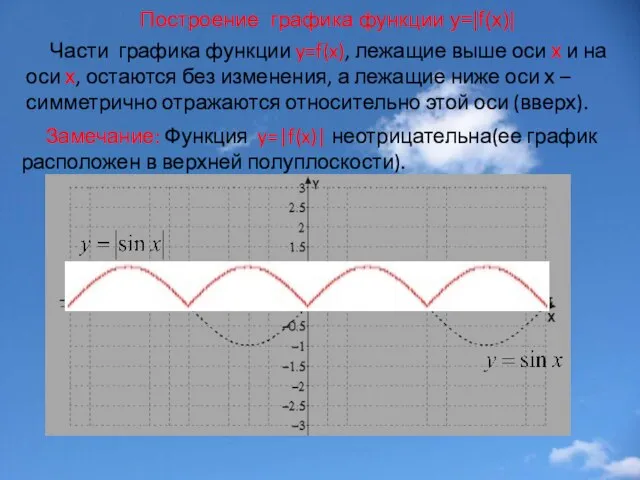
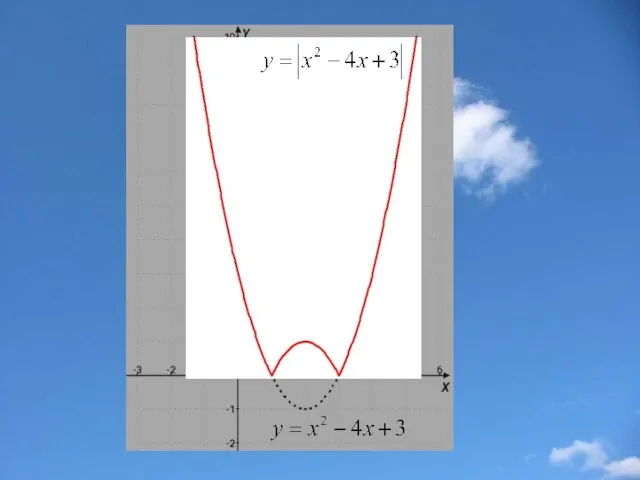
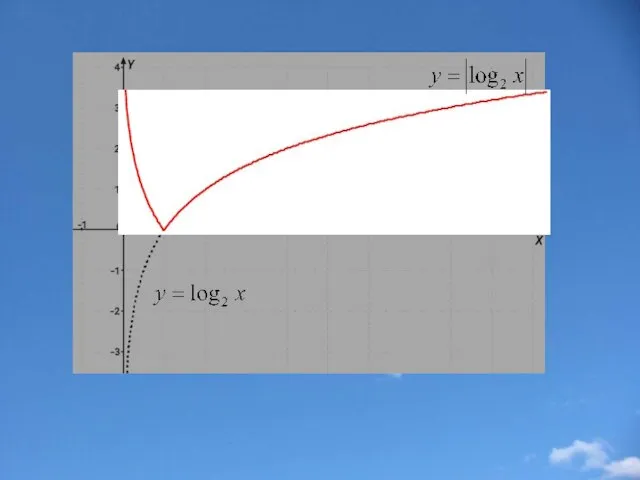
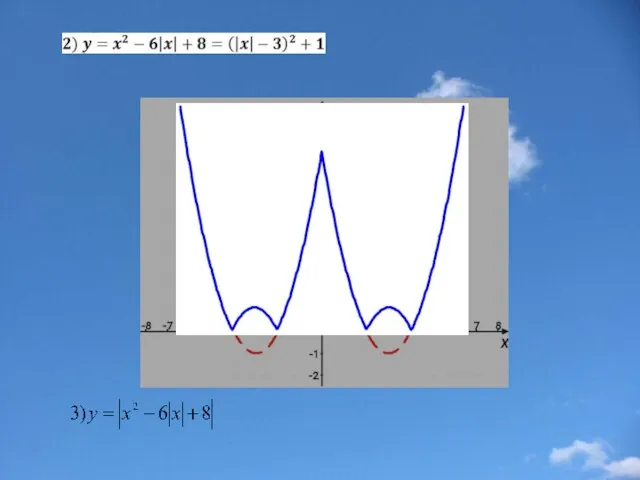
- 21. Построение графика функции у=|f(x)| Части графика функции y=f(x), лежащие выше оси х и на оси х,
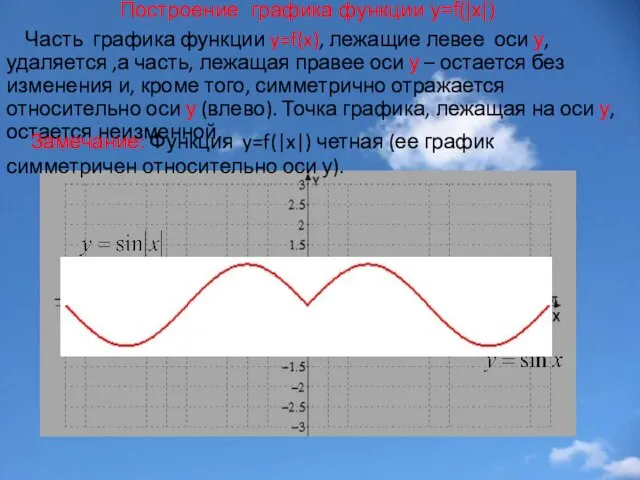
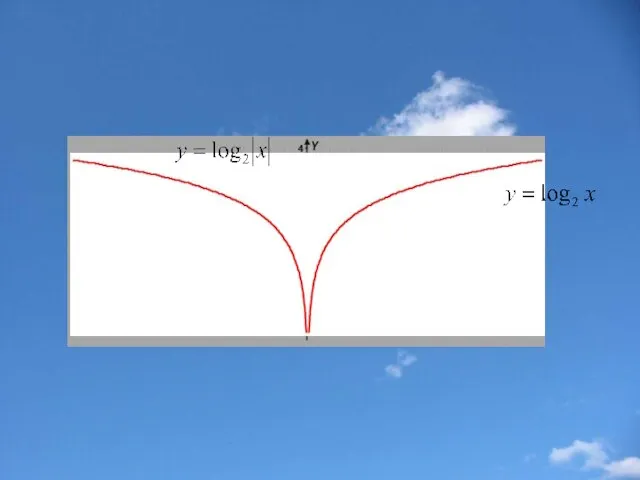
- 24. Построение графика функции у=f(|x|) Часть графика функции y=f(x), лежащие левее оси у, удаляется ,а часть, лежащая
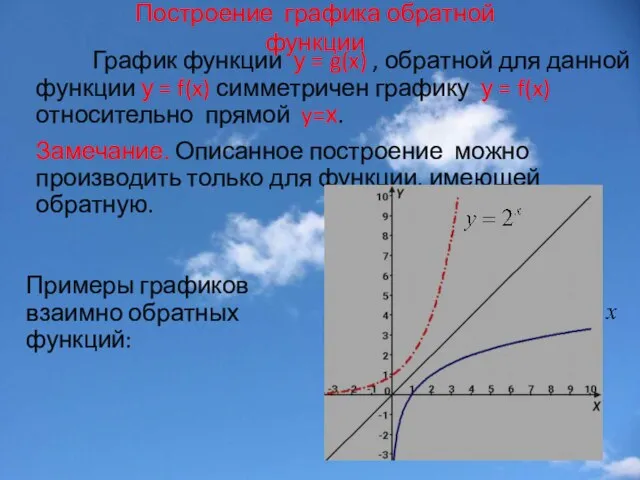
- 28. Построение графика обратной функции График функции у = g(x) , обратной для данной функции у =
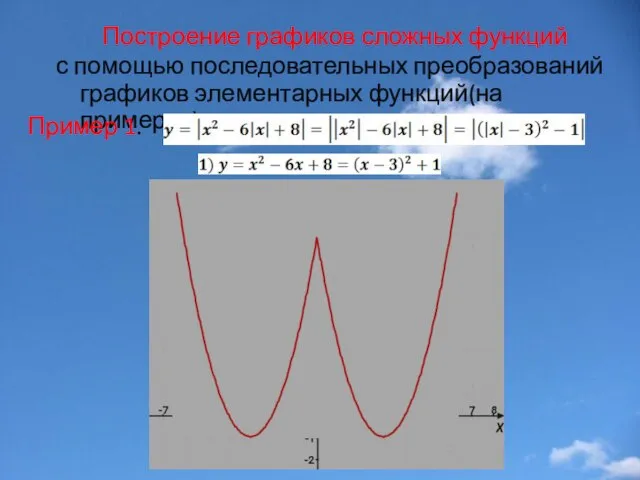
- 31. Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций(на примерах). Пример 1.
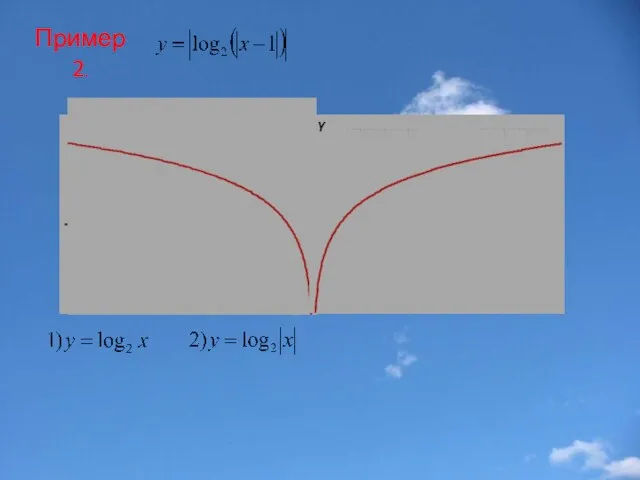
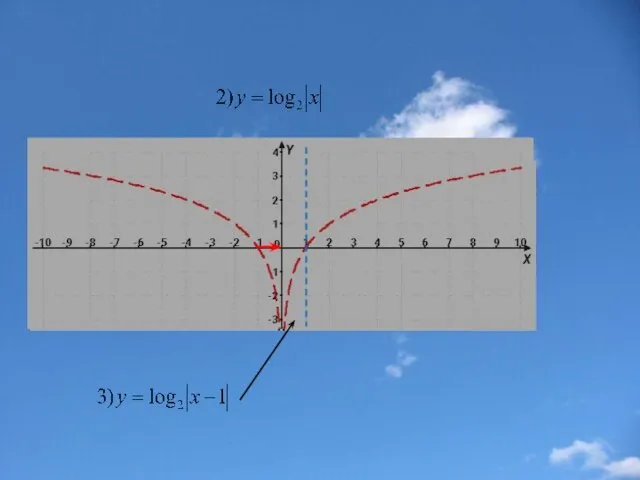
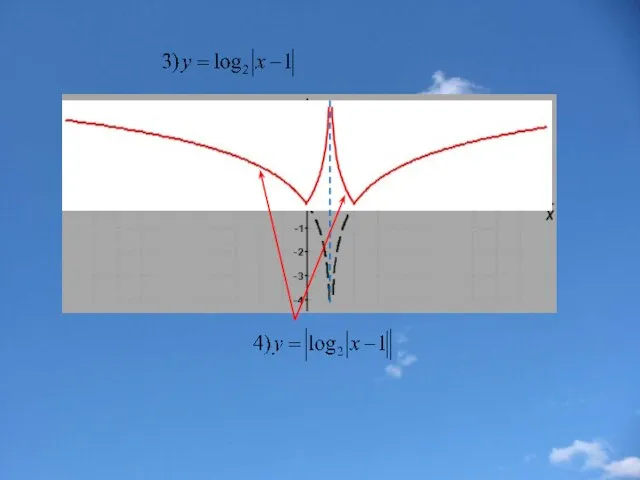
- 33. Пример 2.
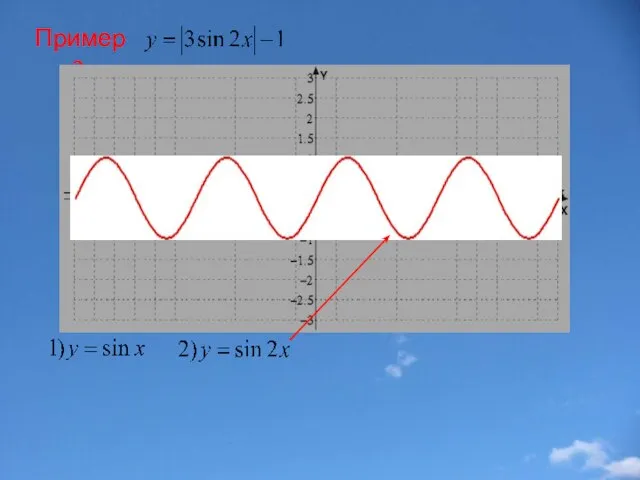
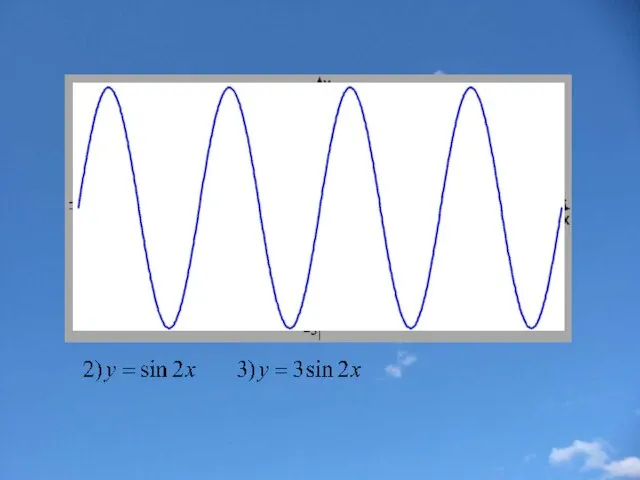
- 36. Пример 3.
- 40. Скачать презентацию











 Учебная практика
Учебная практика Ты и твои товарищи 7 класс
Ты и твои товарищи 7 класс Мастер вышивки Каменщикова Нина Ивановна
Мастер вышивки Каменщикова Нина Ивановна Подвиг «Варяга»
Подвиг «Варяга» Выбор действий при решении задач
Выбор действий при решении задач Перспективы развития мирового газового рынка Наступит ли золотой век газа?
Перспективы развития мирового газового рынка Наступит ли золотой век газа? Ответственность за нарушение режима особо охраняемых природных территорий
Ответственность за нарушение режима особо охраняемых природных территорий Потребности общества в управленческих компетенциях
Потребности общества в управленческих компетенциях Педсовет 7.12.2009“Современные технологии урока- как основа эффективного и качественного образования»
Педсовет 7.12.2009“Современные технологии урока- как основа эффективного и качественного образования» Презентация на тему Достоевский биография
Презентация на тему Достоевский биография  Абонентское обслуживание
Абонентское обслуживание Регенератор RETIGO RG10B
Регенератор RETIGO RG10B ПРЭД Григорович л.1
ПРЭД Григорович л.1 Отель Poseidon, Фиджи
Отель Poseidon, Фиджи В мире информатики
В мире информатики Dream Team - онлайн платформа в IT сфере
Dream Team - онлайн платформа в IT сфере Проблемы управления записями на основе требований международных стандартов на системы менеджмента
Проблемы управления записями на основе требований международных стандартов на системы менеджмента Как получать ответы
Как получать ответы Ильенкова Марина Николаевна. Мастер производственного обучения высшей квалификационной категории 2021 год
Ильенкова Марина Николаевна. Мастер производственного обучения высшей квалификационной категории 2021 год ПРОЕКТ «РАБОЧИЕ НОВОГО ПОКОЛЕНИЯ»
ПРОЕКТ «РАБОЧИЕ НОВОГО ПОКОЛЕНИЯ» Культура стран халифата
Культура стран халифата Администрация Великого Новгорода. Ремонт местных проездов (автомобильных дорог) в 2021 году в рамках проекта Дорога к дому
Администрация Великого Новгорода. Ремонт местных проездов (автомобильных дорог) в 2021 году в рамках проекта Дорога к дому Обзор информационных технологий, используемых в учебном процессе, для демонстраций
Обзор информационных технологий, используемых в учебном процессе, для демонстраций Немцы ворвались в город со стороны станицы Пашковской. В обороне переправы, прикрывая отступление советских войск, участвовали 1
Немцы ворвались в город со стороны станицы Пашковской. В обороне переправы, прикрывая отступление советских войск, участвовали 1 Образовательные семинары для муниципальных образований Томской области
Образовательные семинары для муниципальных образований Томской области Повышение эффективности угольных электростанций
Повышение эффективности угольных электростанций Новинки 2019. Шампунь с маслом пассифлоры
Новинки 2019. Шампунь с маслом пассифлоры Городец: вчера, сегодня, завтра
Городец: вчера, сегодня, завтра