Термодинамика и статистическая физика

План
Идеальные газы
Распределение Больцмана
Распределение Максвелла
Одноатомный идеальный газ
Двухатомный идеальный газ
Многоатомный идеальный газ

Идеальные газы
Идеальный газ – газ, взаимодействие между частицами которого пренебрежимо
слабое взаимодействие на любых расстояниях
разреженный газ
Если нет взаимодействия, то задача сводится к определению уровней энергии 1 молекулы (каноническое распределение)
Вообще, нужно учитывать влияние частиц, находящихся в одинаковом квантовом состоянии
Числа заполнения (число частиц в некотором квантовом состоянии) для идеального газа должна быть малой, а это означает, что в каждом состоянии находится одна частица или частиц нет. Среднее число частиц в квантовом состоянии

Распределение Больцмана .
Вероятность молекуле идеального газа находится в некотором квантовом состоянии, т.е. число молекул в этом состоянии, вида
называется распределением Больцмана (1877 г.)
Коэффициент А находится из условия нормировки для числа частиц (N – полное число молекул в газе)

Распределение Больцмана как следствие большого канонического распределения
Силового взаимодействия нет. У молекул могут быть только обменные эффекты, связанные с тождественностью частиц. Следовательно, можно рассматривать только молекулы в одном и том же квантовом состоянии (только эти частицы будут эквивалентны друг другу). Число частиц и энергия равны
Распределение вероятностей по числу частиц на уровне (числу заполнения)

Распределение Больцмана как следствие большого канонического распределения
Среднее число частиц на уровне для идеального газа
Статистическая сумма равна 1, так как
Окончательно, распределение Больцмана выражается через термодинамическую величину химического потенциала газа

H-теорема Больцмана
Утверждает, что в состоянии равновесия энтропия идеального газа должна иметь максимальное значение
Покажем, что из Н-теоремы следует распределение Больцмана. Пусть на уровне энергии j есть Gj состояний, а Nj – число частиц на уровне. Тогда среднее число частиц на уровне равно
Статистический вес всей системы равен
произведению
Из условия статистики Больцмана следует, что число частиц на уровне должно быть много меньше числа состояний Nj << Gj
Статистический вес одного уровня
имеет вид

Энтропия неравновесного идеального газа и распределение Больцмана
Классическая статистика:

Энтропия неравновесного идеального газа и распределение Больцмана
В равновесии выполняется
первое начало термодинамики
Тогда при условиях
первое начало приводит к
т.е. к распределению Больцмана

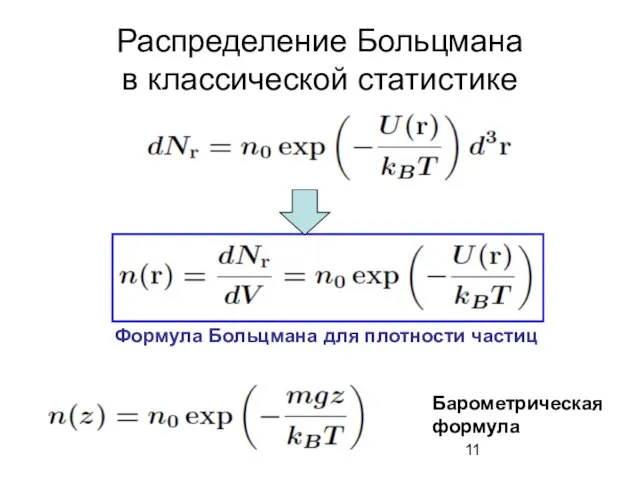
Распределение Больцмана
в классической статистике
Распределение по квантовым состояниям нужно заменить на распределение молекул по фазовому пространству (импульсам и координатам)
Распределение по импульсам и координатам

Распределение Больцмана
в классической статистике
Формула Больцмана для плотности частиц
Барометрическая
формула

Распределение
Максвелла-Больцмана
Энергию молекулы всегда можно разделить на 2 части
а поэтому можно рассматривать отдельно распределение частиц по импульсам (скоростям) поступательного движения (распределение Максвелла) и по внутренним состояниям (распределение Больцмана)
Максвелл
Больцман

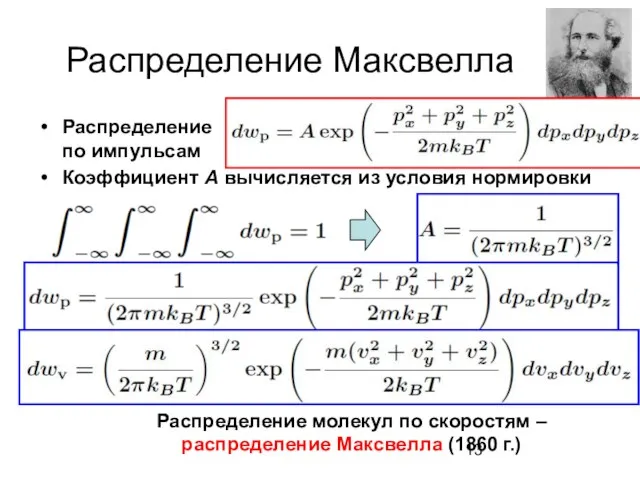
Распределение Максвелла .
Распределение
по импульсам
Коэффициент А вычисляется из условия нормировки
Распределение молекул по скоростям –
распределение Максвелла (1860 г.)

Закон равнораспределения энергии
Среднее значение скорости
Средний квадрат скорости
На каждую квадратичную
степень свободы приходится энергия kT/2

Свободная энергия
идеального газа
Поскольку частицы, по сути, распределены по уровням энергии молекулы, а не по их числу на уровне энергии, то можно применить формулу для статистической суммы канонического распределения
Тогда свободная энергия
В классической статистике

Свободная энергия
идеального газа
Молекула имеет поступательные классические степени свободы и квантовые состояния:
Тогда свободная энергия идеального газа равна

Уравнение состояния
идеального газа
С помощью свободной энергии можно вычислить например, давление газа
Уравнение состояние
любого идеального газа
Энтропия и химический потенциал газа равны
Задание. Запишите термодинамические ограничения
на функцию f(T)

Энергия и теплоемкость идеального газа
Энергия газа, как и его энтальпия, является функцией только температуры (из-за отсутствия взаимодействия изменение объема не сказывается на энергии газа)
Поэтому разность теплоемкостей имеет универсальное значение для любого идеального газа

Закон равнораспределения в классической статистике
В молекуле атомы совершают малые колебания, поэтому потенциальная энергия их взаимодействия является квадратичной функцией координат
Кинетическая энергия – квадратичная функция импульсов, поэтому энергия тоже
квадратичная функция p и q
Число «квадратичных» переменных
одноатомного газа равно l=3
n-атомной нелинейной молекулы равно l=6+2(3n-6)=6n-6
n-атомной линейной молекулы равно l=5+2(3n-5)=6n-5

Закон равнораспределения в классической статистике
В формуле для свободной энергии
уберем температуру в подынтегральном выражении заменой
Тогда

Закон равнораспределения в классической статистике
Тогда
На каждую переменную равная доля энергии kT/2

Распределение молекул по энергии в классической статистике
Объем фазового пространства
Явную зависимость от ε получаем заменой переменных
Задание. Сравните с плотностью состояний, вычисленной
ранее для свободной частицы

Одноатомный идеальный газ
Статистическая сумма в свободной энергии
необходима для расчета внутренней структуры молекул идеального газа ( – кратность вырождения)
Температуру газа считаем много меньше той, что необходима для ионизации газа. Тогда практически будут отсутствовать не только ионизированные, но и возбужденные атомы. Следовательно, можно считать, что все атомы находятся в основном состоянии. В отсутствии орбитального момента и спина (L=S=0) статистическая сумма равна

Теплоемкость одноатомного газа
Итак, свободная энергия
Тогда энтропия газа равна
Внутренняя энергия
Теплоемкость
Отметим, что теплоемкость показывает распределение энергии по поступательным степеням свободы, потому что атомы не возбуждены (в основном состоянии)
Сакур, Тетроде (1912)

Атомы с тонкой структурой
В этом случае атомы обладают вырожденными энергетическими уровнями. Вырождение равно
(2S+1), если L=0
(2L+1)(2S+1) для высоких температур
(2J+1) для низких температур
Ядерным спином обычно можно пренебречь

Применимость статистики Больцмана
Условие применимости следует из малости чисел
что точно выполняется для всех уровней, если
Химический потенциал одноатомного идеального газа равен
Тогда
Окончательно получаем ,где плотность частиц и тепловая длина волны де Бройля

Двухатомный
идеальный газ
Двухатомный газ имеет смысл рассматривать только при температурах, малых по сравнению с энергией диссоциации молекулы (например, для водорода это 52000 градусов)
Рассмотрим ситуацию, когда в основном состоянии молекула не имеет ни орбитального момента, ни спина (L=S=0, т.е. нет вырождения)
Энергия есть сумма электронной, колебательной (ядер) и вращательной (ядер) энергий
электронная
колебательная
вращательная
квант колебаний
момент инерции

Энергия идеального газа

Свободная энергия
Статистическая сумма равна

Свободная энергия
Свободная энергия
поступательная
колебательная
вращательная
электронная

Колебательное движение
Ранее уже было вычислено, что для спектра
статистическая сумма равна
Свободная энергия
позволяет вычислить энергию и теплоемкость

Колебательное движение
При высоких температурах
С
osc
T
квантовая
классическая
NkT/2 на степени свободы
кинетической энергии
NkT/2 на степени свободы потенциальной энергии

Вращательное
движение
Двухатомная молекула
2 различных атома
2 одинаковых атома (перестановка ядер не изменяет состояние!). Примером является
водород Н2.
ортоводород
параводород

Одинаковые .
атомы .
Водород Н2
ортоводород – состояния с большим ядерным стат. весом (кратность вырождения для четных К равна 3/4 для Н2)
параводород – состояния с меньшим ядерным стат. весом (кратность вырождения для нечетных К равна 1/4 для Н2)
Для молекул Н2 с одинаковыми
атомами стат. вес равен
высокие температуры (классический предел)
низкие температуры (одноатомный газ)

Вращательное движение для различных атомов
Низкие температуры
В статистической сумме одной частицы можно оставить только два первых слагаемых
Свободная энергия в том же приближении равна
Теплоемкость экспоненциально уменьшается при приближении температуры к абсолютному нулю

Вращательное движение для различных атомов
Высокие температуры
В статистической сумме нужно учитывать очень много слагаемых, что позволяет перейти от суммирования к интегрированию

Вращательное движение для различных атомов
NkT/2 на первую вращательную
степень свободы
NkT/2 на вторую вращательную
степень свободы
Задание. Вычислите стат. сумму вращения в классической статистике, используя

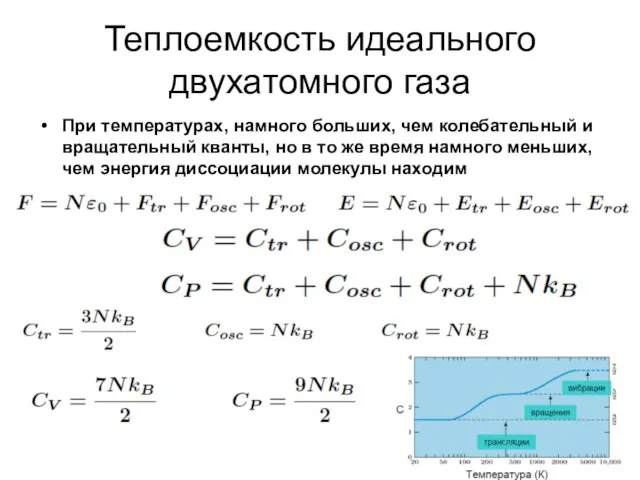
Теплоемкость идеального двухатомного газа
При температурах, намного больших, чем колебательный и вращательный кванты, но в то же время намного меньших, чем энергия диссоциации молекулы находим