Презентация на тему Алгебраические дроби

Тип урока: обобщение.
Цели урока:
Образовательные: а). Обобщение и систематизация знаний учащихся по теме «Алгебраические дроби».
б). Закрепление навыков решения тестовых заданий по данной теме.
Развивающие: а). Формирование и развитие умения мыслить и анализировать.
б). Развитие памяти.
Воспитывающие: а). Воспитание умения работать самостоятельно.
б). Воспитание умения выдерживать регламент времени, отведенного на решение каждого задания.
в). Привитие интереса к предмету.

Повторение основных понятий.
Новые термины математического языка.
Алгебраическая дробь – выражение , где многочлен Р(х)-числитель алгебраической дроби, а Q(х)-ее знаменатель.
2. Основное свойство алгебраической дроби – и числитель и знаменатель алгебраической дроби можно умножить (разделить) на один и тот же не равный 0 многочлен.
3. Рациональное уравнение – уравнение вида =0, где Q(х)≠0.
4. Степень с отрицательным показателем -
,где n – натуральное число и а≠0.

Алгоритм приведения алгебраических дробей к общему знаменателю.
1. Разложить все знаменатели на множители.
2. Найти наименьшее общее кратное для числовых коэффициентов.
3. Составить произведение, включив в него НОК коэффициентов и все буквенные множители. Одинаковые множители берем один раз. Из всех степеней с одинаковым основанием берем множитель с наибольшим показателем степени.
4. Найти дополнительные множители для каждой из дробей.
5. Найти для каждой дроби новый числитель как произведения числителя на дополнительный множитель.
6. Записать каждую дробь с новым числителем и новым (общим) знаменателем.

Упростить выражение:
Первый этап.
4а2-1=(2а-1)(2а+1)
2а2+а=а(2а+1)
Общий знаменатель:
а(2а-1)(2а+1)
Дополнительные множители:
К первой дроби: а
Ко второй дроби: (2а-1)
Второй этап.

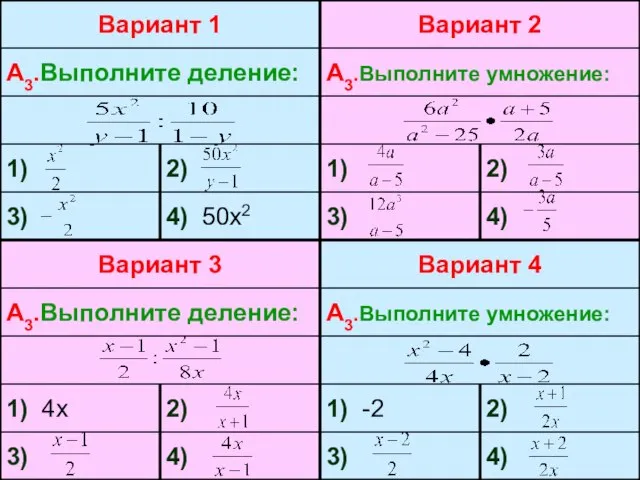
Правила умножения и деления алгебраических дробей, возведения алгебраической дроби в натуральную степень.
Умножение:
Деление:
Возведение в степень:
Например:
1)
2)
3)

Свойства степени с отрицательным целым показателем.
Тождества справедливы для а≠0, b≠0, s,t – произвольные целые числа.
as · at = as + t
as : at = as – t
(as)t = ast
(ab)s = as · bs
(a : b)s = as : bs
Например:
а-3 · а-5 = а-3+(-5) =а-8
а4 : а-3 = а4-(-3) =а7
(а-2)-3 = а-2·(-3) =а6
0,5а2в-2 · (4а-3в3)2 = 0,5а2в-2 · 16а-6в6 = 0,5 · 16 ·(а2а-6) · (в-2в6) = 8а-4в4

Самостоятельная работа.
Выполните тест:
Время работы – 25 минут!

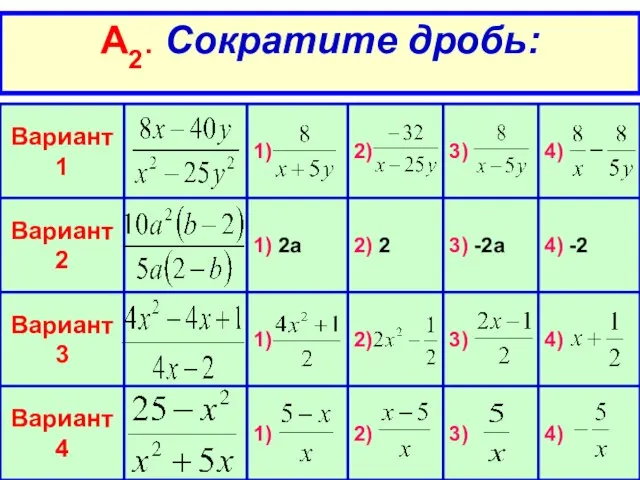
А2. Сократите дробь:

А4. Упростите выражение:

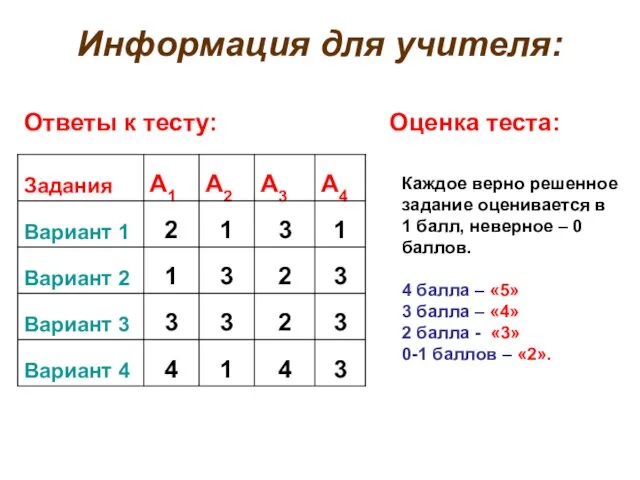
Информация для учителя:
Ответы к тесту: Оценка теста:
Каждое верно решенное задание оценивается в 1 балл, неверное – 0 баллов.
4 балла – «5»
3 балла – «4»
2 балла - «3»
0-1 баллов – «2».