Формирование функциональной грамотности обучающихся

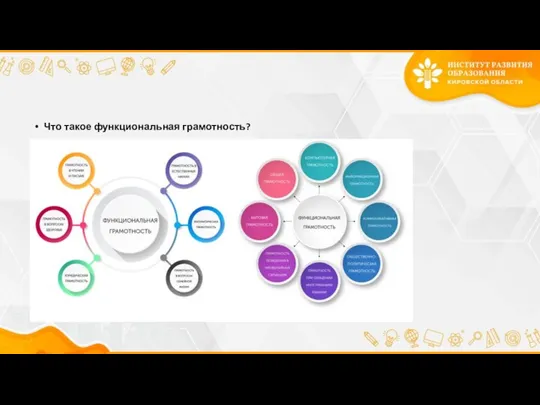
Что такое функциональная грамотность?

http://skiv.instrao.ru/bank-zadaniy/matematicheskaya-gramotnost/

ЦЕЛИ ИЗУЧЕНИЯ УЧЕБНОГО ПРЕДМЕТА
формирование центральных математических понятий (число, величина, геометрическая фигура, переменная, вероятность, функция), обеспечивающих преемственность и перспективность математического образования обучающихся;
подведение обучающихся на доступном для них уровне к осознанию взаимосвязи математики и окружающего мира, понимание математики как части общей культуры человечества;
развитие интеллектуальных и творческих способностей обучающихся, познавательной активности, исследовательских умений, критичности мышления, интереса к изучению математики;
формирование функциональной математической грамотности: умения распознавать проявления математических понятий, объектов и закономерностей в реальных жизненных ситуациях и при изучении других учебных предметов, проявления зависимостей и закономерностей, формулировать их на языке математики и создавать математические модели,
применять освоенный математический аппарат для решения практико-ориентированных задач, интерпретировать и оценивать полученные результаты.

Подходы к оценке математической грамотности учащихся основной школы
«Математическая грамотность – это способность индивидуума проводить математические рассуждения и формулировать, применять, интерпретировать математику для решения проблем в разнообразных контекстах реального мира»
Основа организации исследования математической грамотности
включает три структурных компонента:
− контекст, в котором представлена проблема;
− содержание математического образования, которое используется в
заданиях;
− мыслительная деятельность, необходимая для того, чтобы связать
контекст, в котором представлена проблема, с математическим содержанием, необходимым для её решения.

Контекст задания – это особенности и элементы окружающей
обстановки, представленные в задании в рамках предлагаемой ситуации. Эти ситуации связаны с разнообразными аспектами окружающей жизни и требуют для своего решения большей или меньшей математизации.
Выделены и используются 4 категории контекстов, близкие учащимся: общественная жизнь, личная жизнь, образование/профессиональная деятельность, и научная деятельность

Математическое содержание заданий в исследовании распределено по четырём категориям: пространство и форма, изменение и зависимости, количество, неопределённость и данные, которые охватывают основные типы проблем, возникающих при взаимодействиях с повседневными явлениями. Название каждой из этих категорий отражает обобщающую идею,
которая в общем виде характеризует специфику содержания заданий, относящихся к этой области

Круг математических тем, которые, с одной стороны, изучаются в школьном курсе математики, с другой стороны, необходимы учащимся в качестве основы для жизни и для дальнейшего расширения их математического кругозора:
– изменение и зависимости – задания, связанные с математическим
описанием зависимости между переменными в различных процессах, т.е. с
алгебраическим материалом;
– пространство и форма – задания, относящиеся к пространственным и
плоским геометрическим формам и отношениям, т.е. к геометрическому
материалу;
– количество – задания, связанные с числами и отношениями между
ними, в программах по математике этот материал чаще всего относится к
курсу арифметики;
– неопределённость и данные – задания охватывают вероятностные и
статистические явления и зависимости, которые являются предметом
изучения разделов статистики и вероятности.

Для описания мыслительной деятельности при разрешении предложенных проблем используются следующие глаголы: формулировать, применять и интерпретировать, которые указывают на мыслительные задачи, которые будут решаться учащимися:
– формулировать ситуацию на языке математики;
– применять математические понятия, факты, процедуры;
– интерпретировать, использовать и оценивать математические результаты

Помимо уже названных нововведений исследования, отметим
новые темы, включённые в содержание проверки: − явления роста, изменений линейного и нелинейного характера; например,
потребуется проследить закономерности, проявляющиеся при возведении
в степень некоторого числа;
− геометрические преобразования, аппроксимации, разбиения и составления фигур; например, потребуется построить орнамент из заданных фигур по заданному правилу;
− компьютерное конструирование и моделирование, например, потребуется
изображать по указанным правилам маршруты на карте;
− принятие решений с учётом предлагаемых условий или дополнительной информации; например, потребуется при покупке некоторого
товара учитывать представленное в таблице сообщение, в котором содержится статистика мнений покупателей об этом товаре

Основные элементы содержания
Невысокие результаты российских учащихся связаны с недостаточным овладением некоторым обязательным предметным материалом:
курса математики 5–6-х классов, который не актуализируется в 7–9-х классах (например, действия с обыкновенными и десятичными дробями, проценты, пропорции, отношения);
той части курса математики 9-го класса, который связан с числовыми последовательностями.

Кроме того, проявились недостатки в овладении следующими метапредметными умениями:
• принимать задачу, представленную в форме, отличной от формы, типичной для российских учебников;
• работать с информацией, представленной в различных формах: текстовой, табличной, графической, а также переходить от одной формы к другой;
• привлекать информацию, которая не содержится непосредственно в условии задачи, особенно в тех случаях, когда для этого требуется использовать бытовые сведения, личный жизненный опыт;
• отбирать информацию, необходимую для решения, в частности, если условие задачи содержит избыточную информацию; удерживать в процессе решения все условия, необходимые для решения проблемы;

• владеть навыками самоконтроля за выполнением условий (ограничений) при нахождении решения и интерпретации полученного результата в рамках ситуации;
• определять самостоятельно точность данных, требуемых для решения задачи;
использовать здравый смысл, метод перебора возможных вариантов, метод проб и ошибок;
• представлять в свободной словесной форме обоснованный ответ, который определяется особенностями ситуации.

Умения, на формирование или развитие которых следует обратить внимание при обучении в 5-х классах
– выполнять действия с натуральными числами, с обыкновенными дробями: упорядочение долей, сложение и вычитание несложных дробей;
– выполнять действия с числовыми выражениями; составлять числовое выражение;
– выполнять деление с остатком, иметь представление о делителях и кратных;
– выполнять приближенные вычисления, прикидку и оценку результата вычислений, округлять до указанной разрядной единицы, а также с учётом условий описанной ситуации по недостатку или по избытку;
– распознавать и делать выводы о зависимости между двумя величинами (прямая/обратная); решать задачи на увеличение/уменьшение на/в;
– переводить единицы измерения длины и времени из более крупных в более мелкие и обратно;

– решать задачи методом перебора вариантов;
– читать, заполнять и интерпретировать данные таблиц, столбчатой и круговой диаграмм;
– иметь представление о шкалах; ориентироваться на числовой прямой;
–устанавливать соответствие между реальным размером объекта и представленным на изображении;
– распознавать геометрические формы и описывать объекты окружающего мира с помощью языка геометрии;

– представлять объект по описанию, рисунку, заданным характеристикам; мысленно трансформировать трёхмерную фигуру (реальный объект) в двумерную и обратно, распознавать развертки куба, параллелепипеда;
– складывать фигуры из квадратов, прямоугольников, треугольников, отрезков, разбивать на указанные формы;
–использовать для решения задач простейшие свойства квадрата и прямоугольника;
–иметь представление о площади и периметре, применять формулы нахождения периметра и площади квадрата и прямоугольника;
– проверять истинность утверждений, обосновывать вывод, утверждение, полученный результат.

Умения, на формирование или развитие которых следует обратить внимание при обучении в 7-х классах
– выполнять все виды деятельности, указанные для 5 класса, а также:
– сравнивать рациональные числа, выполнять вычисления с рациональными числами, реальные расчёты;
– вычислять проценты (процентное снижение/повышение), пропорции и отношения, масштаб, использовать основное свойство пропорции, пропорциональное увеличение/уменьшение;
– понимать закономерности, составлять последовательности;
– читать графики зависимостей (линейная и нелинейная);
–составлять математическое описание предложенной зависимости в общем виде (в виде выражения/формулы);

– использовать простейшие свойства треугольника, окружности;
– распознавать комбинации различных плоских форм – отрезков, окружностей, полуокружностей, дуг;
– распознавать трёхмерные фигуры: цилиндр, конус, пирамида (элементы фигур, развертки), комбинации пространственных фигур;
– иметь представление о статистических характеристиках – среднем арифметическом, медиане, моде, размахе, наибольшем и наименьшем значении набора данных;
– интерпретировать данные, представленные в таблицах и на диаграммах, на графиках;
– составлять высказывания, проверять истинность утверждений.

Подходы к составлению заданий, предназначенных для оценки и формирования математической грамотности
1. Учащимся предлагаются не учебные задачи, а контекстуальные, практические проблемные ситуации, разрешаемые средствами математики. Контекст, в рамках которого предложена проблема, должен быть действительно жизненным, а не надуманным. Ситуации должны быть характерными для повседневной учебной и внеучебной жизни учащихся (например, связаны с личными, школьными или общественными проблемами, как это понимается в концепции PISA). Поставленная проблема должна быть нетривиальной, интересной и актуальной для учащихся того возраста, на который она рассчитана.

2. Для выполнения задания требуется холистическое, т.е. целостное, а не фрагментарное, применение математики. Это означает, что требуется осуществить весь процесс работы над проблемой: от понимания, включая формулирование проблемы на языке математики, через поиск и осуществление её решения, до сообщения и оценки результата, а не только часть этого процесса (например, решить уравнение или упростить алгебраическое выражение).
3. Мыслительная деятельность, осуществляемая при выполнении заданий, описывается в соответствии с концепцией PISA-2021.

4. Для выполнения заданий требуются знания и умения из разных разделов курса математики основной школы, соответствующие темам, выделенным в PISA, и планируемым результатам в объёме ФГОС ООО и Примерной основной образовательной программы, формирование которых осуществляется в 5-х или 7-х классах соответственно.
5. Используется следующая структура задания: даётся описание ситуации (введение в проблему), к которой предлагаются два связанных с ней вопроса.

6. Введение в проблему представляет собой небольшой вводный текст, мотивирующего характера, который не содержит лишней информации, не связанной с заданием или не принципиальной для ответа на поставленные далее вопросы. Введение не должно содержать информацию, которая носит отвлекающий характер. Важно: уровень овладения читательской грамотностью не должен отражаться на проверке математической грамотности.
Информация, сообщаемая в задании, даётся в различных формах: числовой, текстовой, графической (график, диаграмма, схема, изображение и др.), она может быть структурирована и представлена в виде таблицы.
Наличие визуализации обязательно. Оказать помощь учащимся в части мысленной визуализации и погружения в сюжет должны фото и рисунки. Графические средства визуализации математического содержания проблемы окажут учащимся помощь на этапе её моделирования, послужат опорой для проведения рассуждений.
Если введение содержит слова, которые могут быть не известны учащимся, то в нём можно дать краткое пояснение, определение и/или иллюстрацию к ним.

7. Вопрос позволяет раскрыть приведённую ситуацию с определённой стороны. Каждый самостоятельный содержательный шаг фиксируются; все основные элементы выделяются для оценивания.
Для выполнения большинства заданий не требуется делать громоздкие вычисления, что позволяет значительно уменьшить влияние вычислительных ошибок на демонстрацию учащимся понимания изученных понятий, применение способов действий для решения поставленных задач. В целях оптимизации вычислений учащимся разрешается использовать калькулятор.
В большинстве заданий не содержится прямых указаний на способ, правило или алгоритм выполнения (решения), что позволяет проверить, насколько осознанно учащиеся применяют полученные знания.
Для ответа на вопрос задания достаточно информации, представленной в описании ситуации; если для ответа на последующие вопросы требуется дополнительная информация, то она сообщается в формулировке вопроса или отдельно. Например, если для выполнения задания требуется использовать формулы, то они приводятся в качестве справочного материала.

8. Учитывается, что задания предлагаются учащимся на компьютере, и ответы они вносят, используя его клавиатуру. При разработке заданий используются возможности компьютера, позволяющие проводить построение заданных математических объектов, переносить на плоскости заданные объекты, выполнять вычисления с заданными числами и др.
9. Используются задания разного типа по форме ответа:
− с выбором одного или нескольких верных ответов из предложенных альтернатив;
− со свободным кратким ответом в форме конкретного числа, одного-двух слов;
− со свободным полным ответом, содержащим запись решения поставленной проблемы, построение заданного геометрического объекта, объяснение полученного ответа.

Характеристика задания
1. Область содержания (всего 4 данные области): пространство и форма; изменение и зависимости; неопределенность и данные; количество.
2. Контекст (всего 4 контекста): общественная жизнь; личная жизнь; образование/профессиональная деятельность; научная деятельность.
3. Мыслительная деятельность (всего 4 деятельности): рассуждать; формулировать; применять; интерпретировать.
4. Объект оценки (предметный результат): например, чтение графиков реальных зависимостей.
5. Уровень сложности: 1, 2 или 3.
6. Формат ответа: с развёрнутым ответом; с выбором ответа; с кратким ответом.
7. Критерии оценивания (1 или 2 балла): полный ответ – 2 балла, частично верный ответ – 1 балл.

Использование заданий для оценки и формирования математической грамотности
Для достижения целей мониторинга математической грамотности предлагается использовать блок заданий, рассчитанный на 20 минут выполнения. Предлагается такая структура блока: 2 задания (сюжета) по 2 вопроса в каждом задании, всего 4 вопроса.
Суммарно в каждый блок входят:
− задания из 2-3-х (из 4-х) областей математического содержания,
− задания из 2-х (из 4-х) контекстов,
− задания из 3-4-х (из 4-х) мыслительных процессов;
− задания трёх видов по сложности: одно лёгкое, два средних, одно сложное;
− задания со следующими критериями оценивания: лёгкое задание оценивается одним баллом, остальные –2-мя баллами; общая сумма баллов за верно выполненный блок заданий – 7.

В целях формирования математической грамотности задания могут использоваться самостоятельно. В этом случае они могут быть дополнены вопросами, развивающими, уточняющими предложенную ситуацию или являющимися проекцией сюжета на реальную жизнь конкретных учащихся, жизнь класса, проблемы местного социума.
Задания лучше выполнять в парах или группах (это зависит от объёмности задания), тогда у учащихся будет возможность обсудить сюжет, используя «коллективный» опыт, уточнить своё понимание ситуации, возможно, задать вопросы учителю. Это поможет выйти на выявление математической сути задания и адекватно сформулировать на языке математики, найти необходимые способы решения.

Обсуждение полезно и на этапе решения задачи, и на этапе интерпретации полученных результатов, чтобы понять, все ли необходимые условия учтены, можно ли решить иначе, проще, рациональнее, соответствует ли математическое решение контексту ситуации и т.п. Обсуждая с классом результаты выполнения задания, учитель должен акцентировать внимание на трёх моментах: как ситуация была преобразована в математическую задачу; какие знания, факты были использованы, какие методы и способы решения были предложены и обсудить их достоинства; как можно оценить полученное решение с точки зрения исходной ситуации.

Полезно предложить учащимся провести анализ своей включенности в выполнение задания, отрефлексировать весь процесс и зафиксировать:
− какие идеи и соображения возникали, были ли они существенными и плодотворными, учтены ли в решении;
− какие возникли трудности и на каком этапе работы над заданием;
− удастся ли самостоятельно справиться с аналогичной ситуацией, если она повторится.
В целях закрепления формируемых умений в качестве домашнего задания можно предложить аналогичную ситуацию с несколько изменёнными данными. Однако задание может носить и творческий характер: придумать своё задание на основе рассмотренного сюжета.
При определённой системности работы по формированию математической грамотности, можно включать изменённые задания и в контрольную работу в качестве дополнительного задания, не связанного с основной темой. В этом случае, можно осуществлять мониторинг выполнения такого рода заданий.