Содержание
- 2. 2 Исследование качества процессов регулирования Одной из проблем, возникающих при построении систем автоматического регулирования, наряду с
- 3. 3 Рис. 8.1. Ошибки регулирования: а) статическая; б) динамическая 4 Перерегулирование σ, измеряемое в % и
- 4. Качество регулирования считается удовлетворительным, если перерегулирование не превышает 30 – 40 %. 5 Степень затухания ψ,
- 5. Иногда требования по качеству регулирования могут быть более жесткие, например, переходный процесс должен быть монотонным или
- 6. Рис. 8.3 определение качества монотонных переходных процессов по степени устойчивости: а - расположение корней характеристического уравнения;
- 7. Рис. 8.4 Определение качества колебательных переходных процессов по степени устойчивости: а - расположение корней характеристического уравнения;
- 8. 2 Степень колебательности так же, как и степень устойчивости, используется и для оценки запаса устойчивости и
- 9. Из последнего соотношения видно, что в системах с П-регулятором статическая ошибка уменьшается с увеличением значения параметра
- 10. 10 Интегральные критерии качества Интегральные критерии качества представляют собой определенные интегралы по времени в пределах от
- 11. Рис. 8.5 Интегральные оценки качества регулирования: а - линейная; б - модульная; в - квадратичная Линейный
- 12. 12 Если перейти к пределу при s → 0, то получим Следует отметить, что для вычисления
- 13. 13 Пример 8.1 Требуется вычислить для системы с передаточной функцией Так как , а 2 Модульный
- 14. 14 3 Интегральный квадратичный критерий (8.9) является наиболее распространенным критерием качества и представляет собой площадь под
- 16. Скачать презентацию
Слайд 22
Исследование качества процессов регулирования
Одной из проблем, возникающих при построении систем автоматического
2
Исследование качества процессов регулирования
Одной из проблем, возникающих при построении систем автоматического

Система автоматического регулирования называется качественной, если она удовлетворяет определенным технологическим требованиям: например, как будет меняться реакция системы, если на ее вход действуют различного рода возмущения как по каналу управления, так и по каналу возмущения, т.е. обеспечивается ли принципиальная возможность прихода системы в некоторое установившееся состояние.
Такое понятие качества автоматической системы охватывает ее статические и динамические свойства, выраженные в количественной форме и получившие название показателей качества управления.
Для оценки качества регулирования в количественной форме используются показатели качества, которые подразделяются на прямые, косвенные, частотные, интегральные.
Показатели качества управления
Прямые показатели:
Наиболее распространенными прямыми показателями или критериями качества, применяемыми в системах управления, являются:
1 Статическая ошибка регулирования ycт, определяемая как разность между установившимся значением регулируемой переменной и ее заданным значением (рис. 8.1а), т.е. yст = yуст– узад.
2 Динамическая ошибка регулирования yдин, определяемая как наибольшее отклонение в
переходном процессе регулируемой переменной от ее установившегося значения (рис. 8.1б).
Слайд 33
Рис. 8.1. Ошибки регулирования: а) статическая; б) динамическая
4 Перерегулирование σ, измеряемое
3
Рис. 8.1. Ошибки регулирования: а) статическая; б) динамическая
4 Перерегулирование σ, измеряемое
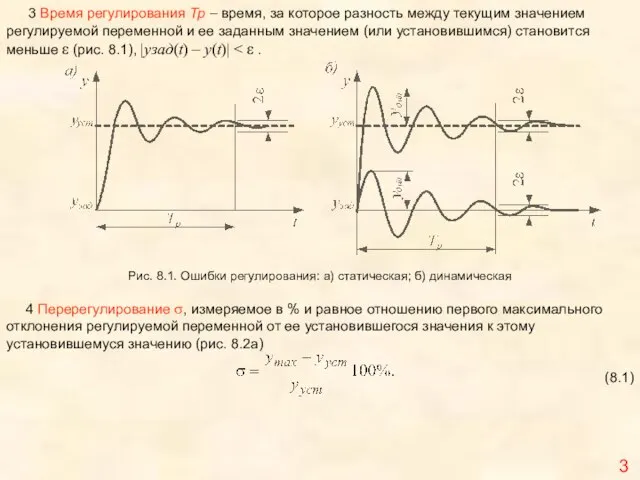
(8.1)
3 Время регулирования Тр – время, за которое разность между текущим значением регулируемой переменной и ее заданным значением (или установившимся) становится меньше ε (рис. 8.1), |узад(t) – у(t)| < ε .
Слайд 4 Качество регулирования считается удовлетворительным, если перерегулирование не превышает 30 – 40
Качество регулирования считается удовлетворительным, если перерегулирование не превышает 30 – 40
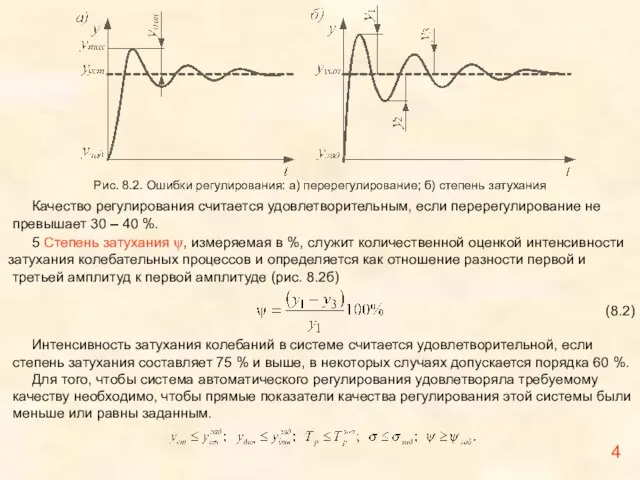
5 Степень затухания ψ, измеряемая в %, служит количественной оценкой интенсивности
затухания колебательных процессов и определяется как отношение разности первой и третьей амплитуд к первой амплитуде (рис. 8.2б)
(8.2)
Интенсивность затухания колебаний в системе считается удовлетворительной, если степень затухания составляет 75 % и выше, в некоторых случаях допускается порядка 60 %.
Для того, чтобы система автоматического регулирования удовлетворяла требуемому качеству необходимо, чтобы прямые показатели качества регулирования этой системы были меньше или равны заданным.
4
Рис. 8.2. Ошибки регулирования: а) перерегулирование; б) степень затухания
Слайд 5 Иногда требования по качеству регулирования могут быть более жесткие, например, переходный
Иногда требования по качеству регулирования могут быть более жесткие, например, переходный

Прямые показатели качества удобно использовать в тех случаях, когда имеется график переходного процесса y(t), который может быть получен экспериментально в реальной системе регулирования или путем моделирования на ЭВМ. Если же такой возможности нет, т.е. не удается никаким образом получить кривую переходного процесса, то пользуются косвенными показателями качества, которые вычисляются без построения графика переходного процесса по коэффициентам уравнений или по частотным характеристикам.
5
Косвенные показатели качества
Основную группу среди косвенных показателей качества составляют корневые показатели качества регулирования, к которым относятся степень устойчивости и степень колебательности. С точки зрения качества регулирования можно сделать следующие выводы.
1 Степень устойчивости характеризует интенсивность затухания наиболее медленно затухающей неколебательной составляющей переходного процесса, которая
определяется как yк(t) = Ске–ηt. Пусть рассматриваемая система описывается дифференциальным уравнением второго порядка, характеристическое уравнение которого имеет два действительных различных корня s1 = – α1, s2 = – α2 и α1 < α2 (рис. 8.3а). Последним соответствуют две элементарные составляющие свободного движения системы (рис. 8.3б).
Как видно из графиков переходных процессов, чем меньше абсолютное значение корня характеристического уравнения, тем медленнее затухает соответствующая ему составляющая.
Слайд 6Рис. 8.3 определение качества монотонных переходных процессов по степени устойчивости:
а - расположение
Рис. 8.3 определение качества монотонных переходных процессов по степени устойчивости:
а - расположение

Результирующий переходный процесс y(t) = Σ yi (t) . Его затухание определяется наиболее медленно затухающей составляющей, т.е. наименьшим по абсолютному значению корнем характеристического уравнения.
Если же характеристическое уравнение системы имеет комплексные сопряженные корни, то составляющая переходного процесса yi(t) будет иметь колебательный характер
yi(t) = Сie–ηtcosωt и действительная часть корня, а фактически степень устойчивости η = α, характеризует огибающую (рис. 8.4).
5
Слайд 7 Рис. 8.4 Определение качества колебательных переходных процессов по степени устойчивости:
а -
Рис. 8.4 Определение качества колебательных переходных процессов по степени устойчивости:
а -
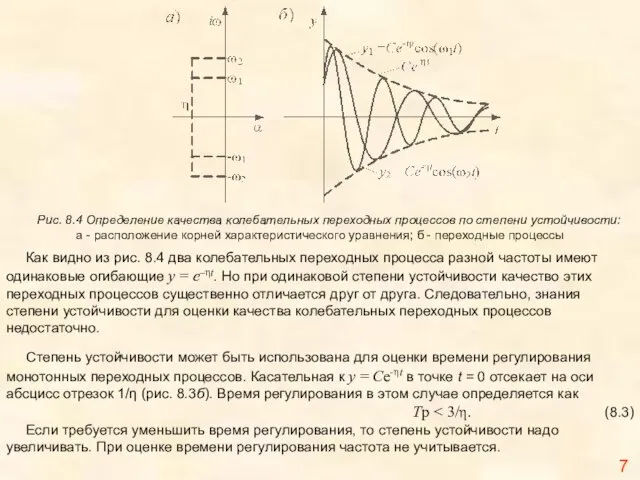
Как видно из рис. 8.4 два колебательных переходных процесса разной частоты имеют одинаковые огибающие y = е–ηt. Но при одинаковой степени устойчивости качество этих переходных процессов существенно отличается друг от друга. Следовательно, знания степени устойчивости для оценки качества колебательных переходных процессов недостаточно.
7
Степень устойчивости может быть использована для оценки времени регулирования монотонных переходных процессов. Касательная к y = Cе-ηt в точке t = 0 отсекает на оси абсцисс отрезок 1/η (рис. 8.3б). Время регулирования в этом случае определяется как
Tp < 3/η. (8.3)
Если требуется уменьшить время регулирования, то степень устойчивости надо увеличивать. При оценке времени регулирования частота не учитывается.
Слайд 8 2 Степень колебательности так же, как и степень устойчивости, используется и
2 Степень колебательности так же, как и степень устойчивости, используется и

(8.4)
Степень колебательности характеризует затухание наиболее медленно затухающей составляющей y(t) = Ae–mωtsinωt, откуда следует, что изменение частоты влечет и изменение амплитуды колебаний.
Степень колебательности однозначно связана со степенью затухания. Действительно, в момент времени t0 амплитуда свободной составляющей определяется как , а в момент времени t0 + Т, т.е. через период, . В этом случае степень затухания, согласно (8.2), запишется
(8.4)
так как T = 2π/ω, ψ = 1 – e−2πm
Степень затухания изменяется от 0 до 1, а степень колебательности - от 0 до ∞. Наиболее часто используются следующие их значения: m = 0,141 (ψ = 0,61); m = 0,221 (ψ = 0,75); m = 0,366 (ψ = 0,9); m = 0,478 (ψ = 0,95).
8
Слайд 9 Из последнего соотношения видно, что в системах с П-регулятором статическая ошибка
уменьшается
Из последнего соотношения видно, что в системах с П-регулятором статическая ошибка
уменьшается

В заключение следует заметить, что динамическая ошибка корневыми методами не оценивается.
9
3 Оценка статической ошибки может быть получена по предельной теореме
(8.5)
где передаточная функция замкнутой системы по каналу ошибки; X(s) - изображение задающего воздействия, в большинстве случаев x(t) = С = const и X(s) = С/s.
С учетом вышесказанного
Например, для систем с интегральным регулятором статическая ошибка отсутствует
а для систем с пропорциональным регулятором равна
Если в Wоб(s) коэффициент передачи равен k, то
Слайд 1010
Интегральные критерии качества
Интегральные критерии качества представляют собой определенные интегралы по
10
Интегральные критерии качества
Интегральные критерии качества представляют собой определенные интегралы по

1 Линейный интегральный критерий
(8.6)
служит для оценки качества неколебательных процессов. Геометрически этот критерий характеризует площадь, заключенную между кривой переходного процесса и осью абсцисс (рис. 8.5а), он учитывает как время регулирования, так и величину динамических отклонений. Если неизвестна кривая переходного процесса, но известна передаточная функция замкнутой системы Wзамк(s) и входная переменная x(t) = 1(t), то значение линейного интегрального критерия определяется с использованием теоремы о конечном значении функции. Действительно, формулу (8.6) можно записать иначе
и тогда
Слайд 11 Рис. 8.5 Интегральные оценки качества регулирования: а - линейная; б -
Рис. 8.5 Интегральные оценки качества регулирования: а - линейная; б -
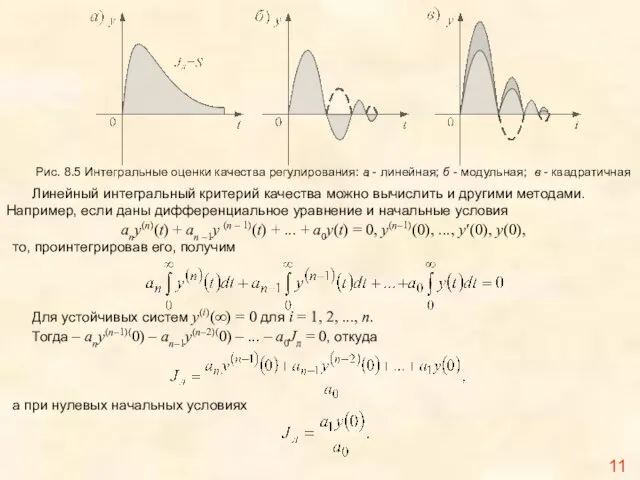
Линейный интегральный критерий качества можно вычислить и другими методами. Например, если даны дифференциальное уравнение и начальные условия
any(n)(t) + an –1y (n – 1)(t) + ... + a0y(t) = 0, y(n–1)(0), ..., y′(0), y(0),
то, проинтегрировав его, получим
Для устойчивых систем y(i)(∞) = 0 для i = 1, 2, ..., n.
Тогда – any(n–1)(0) – an–1y(n–2)(0) – ... – a0Jл = 0, откуда
а при нулевых начальных условиях
11
Слайд 1212
Если перейти к пределу при s → 0, то получим
Следует
12
Если перейти к пределу при s → 0, то получим
Следует

Существуют модификации линейного интегрального критерия, которые применяются в тех случаях, когда начальный участок переходного процесса является менее ответственным, например,
Выведем формулу, позволяющую вычислять такой критерий. Для этого продифференцируем по s функцию
осуществляющую преобразование по Лапласу функции y(t)
Слайд 1313
Пример 8.1
Требуется вычислить для системы с передаточной функцией
Так как , а
13
Пример 8.1
Требуется вычислить для системы с передаточной функцией
Так как , а

2 Модульный интегральный критерий
(8.7)
применяется для оценки качества колебательных процессов, а для неколебательных процессов он совпадает с линейным интегральным критерием. Для его вычисления требуется знание переходного процесса. На практике этот критерий используется при численном исследовании систем на моделях с применением вычислительной техники, т.е. там, где операция взятия модуля не представляет трудности.
Геометрически критерий равен площади, заключенной между кривой y(t) и осью абсцисс (рис. 8.5б).
В некоторых случаях используют модификацию модульного интегрального критерия
которая придает больший вес значениям переходного процесса в его конце.
Слайд 1414
3 Интегральный квадратичный критерий
(8.9)
является наиболее распространенным критерием качества и представляет собой
14
3 Интегральный квадратичный критерий
(8.9)
является наиболее распространенным критерием качества и представляет собой

Стремясь минимизировать (8.9), фактически минимизируют наибольшие отклонения регулируемой величины, поэтому минимальные значения критерия всегда соответствуют колебательным процессам с малым затуханием. С целью устранения этого недостатка применяют улучшенную квадратичную оценку
(8.10)
которая, кроме самих отклонений, учитывает с весовым коэффициентом их производную. Весовой коэффициент выбирается равным желаемому времени нарастания или применяется в пределах
Tр/6 ≤ Т ≤ Tр/3, (8.11)
где Тр - желаемая длительность переходного процесса.
Квадратичный критерий, как и линейный, можно вычислить без построения переходного процесса по частотной характеристике замкнутой системы и преобразованию по Фурье от входного сигнала. Используя формулу Релея, получают
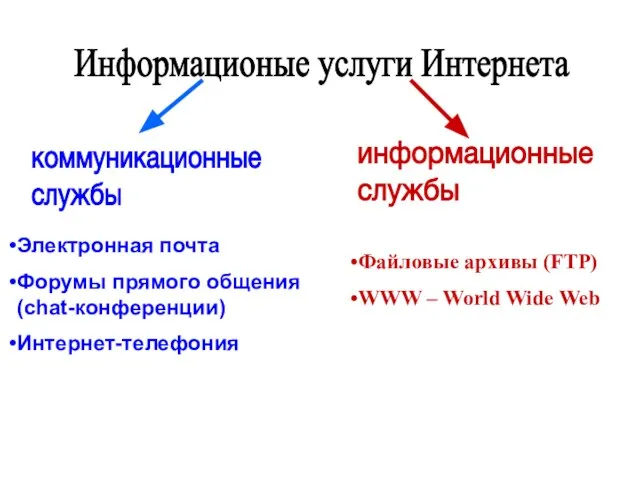 Информационые услуги Интернета
Информационые услуги Интернета МЕТОД УЧЕБНЫХ ПРОЕКТОВ
МЕТОД УЧЕБНЫХ ПРОЕКТОВ Исторические этапы развития коммуникаций. Общинная коммуникационная система
Исторические этапы развития коммуникаций. Общинная коммуникационная система Бизнес-проект: Линия Горизонта
Бизнес-проект: Линия Горизонта Действия с информацией. Хранение информации (5 класс)
Действия с информацией. Хранение информации (5 класс) Назови правильно
Назови правильно Приближенные значения. Округление чисел
Приближенные значения. Округление чисел Фотоотчет распространения промотиража газеты Маяк
Фотоотчет распространения промотиража газеты Маяк Корабельные строения
Корабельные строения Российский экономический кризис:пространственное измерение
Российский экономический кризис:пространственное измерение 15 советов абитуриенту
15 советов абитуриенту Мордовская народная вышивка
Мордовская народная вышивка ITEP-TWAC FACILITY PROGRESS REPORT
ITEP-TWAC FACILITY PROGRESS REPORT Слова о полку Игореве
Слова о полку Игореве Что такое энергоэффективный дом.
Что такое энергоэффективный дом. ООО МПК «СОАР»
ООО МПК «СОАР» Вайшнава-таттва
Вайшнава-таттва Сотовый телефон
Сотовый телефон Магнит на холодильник из пластиковой бутылки
Магнит на холодильник из пластиковой бутылки Композиция в фотографии
Композиция в фотографии ПОЛОЖЕНИЕ о выборах членовМолодежного парламентаМО «Увинский район»
ПОЛОЖЕНИЕ о выборах членовМолодежного парламентаМО «Увинский район» Горный Дагестан
Горный Дагестан Победе в Великой Отечественной войне посвящается
Победе в Великой Отечественной войне посвящается Основы электротехники
Основы электротехники Волонтёрское движение
Волонтёрское движение ФГБОУ ВО Курская ГСХА. Экономический факультет
ФГБОУ ВО Курская ГСХА. Экономический факультет Обобщающий урок.Решение уравнений.
Обобщающий урок.Решение уравнений. Азбука здоровья
Азбука здоровья