Содержание
- 2. Повторить основное свойство дроби и рассмотреть это свойство для алгебраических дробей; Научиться сокращать и приводить дроби
- 3. Изучение новой темы Понятие основного свойства дроби известно из курса 6-го класса (сокращение дробей). Кравченко Г.
- 4. Кравченко Г. М. Над алгебраическими дробями можно осуществлять преобразования аналогичные тем, которые указали для обыкновенной дроби.
- 5. Кравченко Г. М. Внимание! Следствие из основного свойства дроби (изменение знаков у числителя и знаменателя)
- 6. Кравченко Г. М. Решение Для этого найдем дополнительные множители для каждой дроби. Это числа 5 и
- 7. Кравченко Г. М. Решение Для этого найдем дополнительные множители для каждой дроби. Это числа 3b и
- 8. Кравченко Г. М. Решение Для этого найдем дополнительные множители для каждой дроби. Это многочлены - (x
- 9. Кравченко Г. М. Преобразуйте заданные тройки алгебраических выражений так, чтобы получились дроби с одинаковыми знаменателями: Пример
- 10. Кравченко Г. М. Преобразуйте заданные тройки алгебраических выражений так, чтобы получились дроби с одинаковыми знаменателями: Пример
- 11. Кравченко Г. М. Сократите данные дроби: 1 1 1 1 1 1 1 1
- 12. Кравченко Г. М. Сократите дробь: 1 1 1 1 1 1
- 14. Скачать презентацию









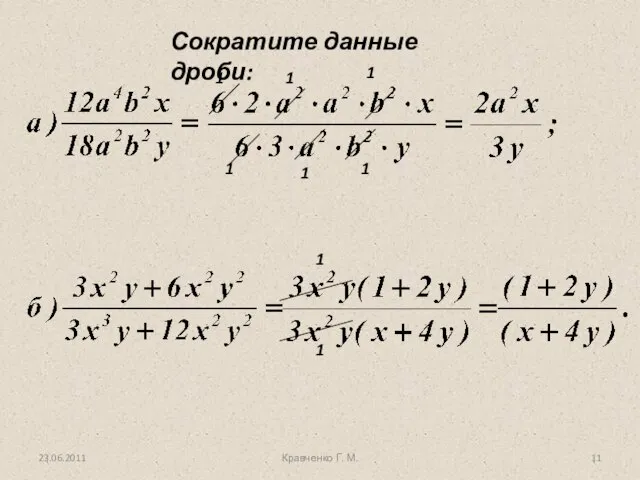
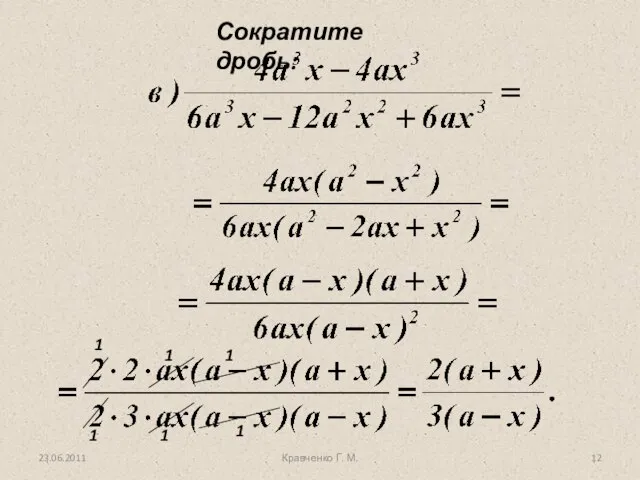
 Приемы компрессии текста
Приемы компрессии текста  Восприятие при длительном общении. Эмпатия, идентификация, рефлексия, атрибуция, аттракция
Восприятие при длительном общении. Эмпатия, идентификация, рефлексия, атрибуция, аттракция Азбука Красноярья
Азбука Красноярья Управление организациями. Теоретические положения процессного подхода
Управление организациями. Теоретические положения процессного подхода What colour is it?
What colour is it? A new educational future - Новое образовательное будущее
A new educational future - Новое образовательное будущее Мотивация как функция менеджмента
Мотивация как функция менеджмента Мои компетенции в сфере управления
Мои компетенции в сфере управления Суша планеты
Суша планеты Научно-методические принципы организации подготовки преподавателей естественнонаучных дисциплин к профессиональной деятельн
Научно-методические принципы организации подготовки преподавателей естественнонаучных дисциплин к профессиональной деятельн Костюм Чеховской эпохи
Костюм Чеховской эпохи Практические методы и руководство по вычислению параметров трещиностойкости конструкций с применением систем MSC.Software
Практические методы и руководство по вычислению параметров трещиностойкости конструкций с применением систем MSC.Software OpenOffice
OpenOffice Слово и время
Слово и время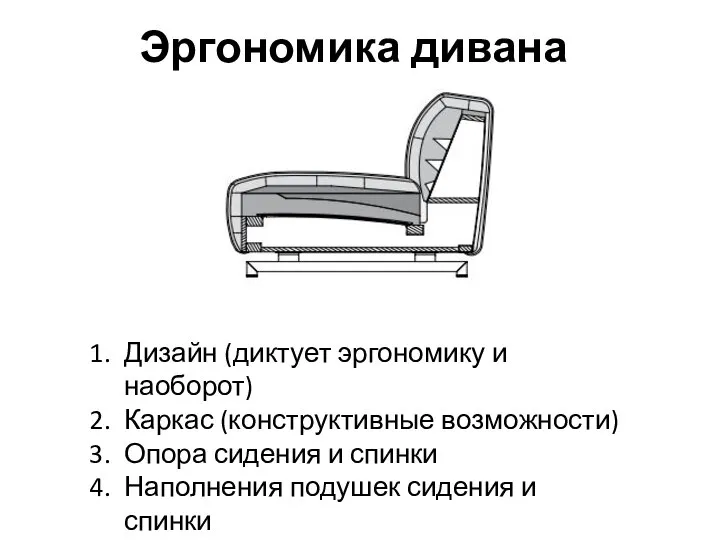 Эргономика дивана
Эргономика дивана Презентация на тему Площадь прямоугольника
Презентация на тему Площадь прямоугольника Заикание.
Заикание. Лекции 6 - 7
Лекции 6 - 7 Презентация на тему Новое время:Встреча Европы и Америки Программа А.Плешакова Окружающий мир 4 класс
Презентация на тему Новое время:Встреча Европы и Америки Программа А.Плешакова Окружающий мир 4 класс  Свето-теневой рисунок. Курс Кинооператорство
Свето-теневой рисунок. Курс Кинооператорство ПРЕДМЕТЫ ДОМАШНЕГО ОБИХОДА
ПРЕДМЕТЫ ДОМАШНЕГО ОБИХОДА Изучаем среднее арифметическое
Изучаем среднее арифметическое Автомобили - старинные и современные
Автомобили - старинные и современные Репродукции картин русских художников
Репродукции картин русских художников Фланцевое соединение
Фланцевое соединение Приглашаем на работу
Приглашаем на работу Методики применения средств физической культуры для направленной коррекции телосложения
Методики применения средств физической культуры для направленной коррекции телосложения Jak uczyć wyłącznie po polsku
Jak uczyć wyłącznie po polsku